

Up: The central black hole
Subsections
From the high 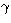 -ray luminosity (assuming isotropic emission) and
Eddington-limit, one can derive the central black hole mass expression,
-ray luminosity (assuming isotropic emission) and
Eddington-limit, one can derive the central black hole mass expression,
| 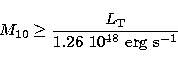 |
(8) |
where, 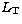 is the bolometric luminosity for emission in the Thomson region,
M10 is the central black hole mass in units of 10
is the bolometric luminosity for emission in the Thomson region,
M10 is the central black hole mass in units of 10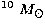 .
The derived masses are as high as 10
.
The derived masses are as high as 10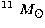 for some
for some 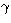 -ray
loud blazars,
PKS 0528+134, PKS 1406-074, and PKS 1622-297 for instance (see Col. 10
in Table 1).
However, for high energy
-ray
loud blazars,
PKS 0528+134, PKS 1406-074, and PKS 1622-297 for instance (see Col. 10
in Table 1).
However, for high energy 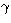 -ray emission, Klein-Nishina effects
must be considered. D&G considered the effect and
obtained an expression for the black hole mass, i.e. their Eq. (16b),
-ray emission, Klein-Nishina effects
must be considered. D&G considered the effect and
obtained an expression for the black hole mass, i.e. their Eq. (16b),
| ![\begin{displaymath}
M_{8}^{\rm KN} \geq {\frac{3\pi d_{\rm L}^{2}(m_{\rm e}c^{2}...
...},\varepsilon_{\rm u})}{1+z}}
\ln[2\varepsilon_{\rm l}(1+z)]
\end{displaymath}](/articles/aas/full/1999/07/ds7917/img54.gif) |
(9) |
where 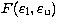 is the integrated photon flux
in units of 10-6 photon cm-2 s-1 between photon energies
is the integrated photon flux
in units of 10-6 photon cm-2 s-1 between photon energies
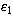 and
and 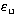 in units of 0.511 MeV.
For the objects considered here,
in units of 0.511 MeV.
For the objects considered here, 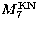 is obtained and
shown in Col. 9 in Table 1. Table 1 shows that the masses obtained from
our consideration and those estimated from the D&G method are
acceptably similar except for 1622-297 and two low redshift BL Lac
objects (Mkn 501 and BL Lacertae). For 1622-297 our value is about
7 times less than that estimated from the D&G method. If we adopt the
flux density
is obtained and
shown in Col. 9 in Table 1. Table 1 shows that the masses obtained from
our consideration and those estimated from the D&G method are
acceptably similar except for 1622-297 and two low redshift BL Lac
objects (Mkn 501 and BL Lacertae). For 1622-297 our value is about
7 times less than that estimated from the D&G method. If we adopt the
flux density 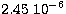 photon cm-2 s-1
for 1622-297 instead of
the peak value as did Muhkerjee et al. (1997) and Fan et al. (1998a), then
the isotropic luminosity is
photon cm-2 s-1
for 1622-297 instead of
the peak value as did Muhkerjee et al. (1997) and Fan et al. (1998a), then
the isotropic luminosity is 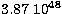 erg s-1.
This luminosity suggests that the Doppler factor and mass
obtained from relations (4) and (7) are respectively 5.01 and 2.41 M7,
and the mass estimated from the D&G is then 3.61 M7. The two
masses are quite similar in this case. For Mkn 501 and BL
Lacertae, our value is much greater than that estimated from the D&G method.
For 3C 279, our results show that the estimated central black hole masses,
4.74 M7 and 3.43 M7 for 1991 and 1996 flares respectively,
are almost the same, while the masses estimated from the D&G method are
1.92 M7 and 7.53 M7 for 1991 and 1996 flares respectively.
Table 1 (also see relation (9)) shows that the mass obtained from the D&G
method is sensitive to the flux, variable flux gives different mass for a
source. The mass obtained from our method does not depend on the flux
so sensitively. For 3C 279 1991 and 1996 flares, masses obtained from
our consideration are almost the same while those obtained from the D&G
method show a difference of more or less a factor of 4. But our method
depends on the timescales (see relation 4). Since we only considered
the objects showing short timescales (hours) in the present paper,
the masses obtained are in a range of (1
erg s-1.
This luminosity suggests that the Doppler factor and mass
obtained from relations (4) and (7) are respectively 5.01 and 2.41 M7,
and the mass estimated from the D&G is then 3.61 M7. The two
masses are quite similar in this case. For Mkn 501 and BL
Lacertae, our value is much greater than that estimated from the D&G method.
For 3C 279, our results show that the estimated central black hole masses,
4.74 M7 and 3.43 M7 for 1991 and 1996 flares respectively,
are almost the same, while the masses estimated from the D&G method are
1.92 M7 and 7.53 M7 for 1991 and 1996 flares respectively.
Table 1 (also see relation (9)) shows that the mass obtained from the D&G
method is sensitive to the flux, variable flux gives different mass for a
source. The mass obtained from our method does not depend on the flux
so sensitively. For 3C 279 1991 and 1996 flares, masses obtained from
our consideration are almost the same while those obtained from the D&G
method show a difference of more or less a factor of 4. But our method
depends on the timescales (see relation 4). Since we only considered
the objects showing short timescales (hours) in the present paper,
the masses obtained are in a range of (1  7)
7) 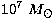 .
.
To fit 3C 279 multiwavelength energy spectrum corresponding to 1991
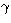 -ray flare, Hartman employed an accreting black hole of
-ray flare, Hartman employed an accreting black hole of
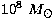 , our result of
, our result of 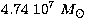 is similar to
theirs.
is similar to
theirs.
To explain the extremely high and violently variable luminosity of AGNs, the
beaming model has been proposed. In this model, the Lorentz factor, 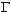 , and the viewing angle,
, and the viewing angle, 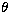 , are not measurable, but they can be
obtained through the measurement of superluminal velocity,
, are not measurable, but they can be
obtained through the measurement of superluminal velocity, 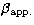 ,
and the determination of Doppler factor,
,
and the determination of Doppler factor, 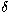 , which are related with
the two unmeasurable parameters,
, which are related with
the two unmeasurable parameters, 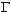 and
and 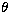 , in the forms:
, in the forms:
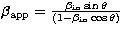 ,
, 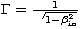 , and
, and
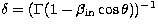 . So,
. So,
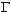 and
and 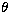 can be obtained from the following relations:
can be obtained from the following relations:
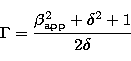
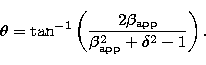
From our previous work (Fan et al. 1996), we can get superluminal
velocities for
3C 279 and BL Lacertae. When the superluminal velocities and
the derived Doppler factor are substituted to the above two relations.
we found that: For 3C 279, 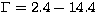 and
and
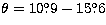 for
for 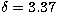 ; and
; and 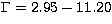 and
and
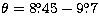 for
for 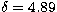 .
For BL Lacertae
.
For BL Lacertae 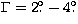 and
and 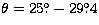 .
.
To let the optical depth (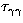 ) be less than unity,
Doppler factor in
) be less than unity,
Doppler factor in 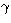 -ray region has been obtained for some objects
by other authors.
-ray region has been obtained for some objects
by other authors.
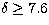 for Q1633+382 (Mattox et al. 1993);
for Q1633+382 (Mattox et al. 1993);
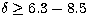 for 3C 279 1996 flare (Wehrle et al. 1998) and
for 3C 279 1996 flare (Wehrle et al. 1998) and 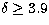 for
3C 279 1991 flare (Mattox et al. 1993),
for
3C 279 1991 flare (Mattox et al. 1993), 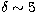 is also
obtained by Henri et al. (1993);
is also
obtained by Henri et al. (1993);
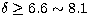 for
PKS 1622-297 (Mattox et al. 1997). Our results in Table 1 are consistent
with
those results.
for
PKS 1622-297 (Mattox et al. 1997). Our results in Table 1 are consistent
with
those results.
In this paper, the central mass and Doppler factor are obtained for 8
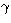 -ray loud blazars with available short
-ray loud blazars with available short 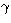 -ray timescales.
The mass obtained from relation (4) in the present paper is compared with
that obtained from the D&G method, the masses obtained from two methods
are similar for 5 out of 8 objects. Our method is not as sensitive to the flux
as the D&G method in estimating the central black hole mass.
The masses obtained here are in a range of
(1
-ray timescales.
The mass obtained from relation (4) in the present paper is compared with
that obtained from the D&G method, the masses obtained from two methods
are similar for 5 out of 8 objects. Our method is not as sensitive to the flux
as the D&G method in estimating the central black hole mass.
The masses obtained here are in a range of
(1  7)
7) 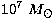 , which stems from the fact that the time
scales considered here are in a range of 3.2 to 24 hours.
For 3C 279, the masses obtained from the two flares are almost the same.
For 3C 279 and BL Lacertae, the Lorentz factor and viewing
angle are estimated.
, which stems from the fact that the time
scales considered here are in a range of 3.2 to 24 hours.
For 3C 279, the masses obtained from the two flares are almost the same.
For 3C 279 and BL Lacertae, the Lorentz factor and viewing
angle are estimated.
Acknowledgements
The authors thank the referee Dr. S.D. Bloom
for his comments and suggestions. J.H.F. thanks Drs. B ttcher,
Dermer,
Carter-Lewis, Catanese, Ghisellini, Kataoka, and Wagner for their sending him
their publications and information and the Education fund
of Guangzhou City for support. This work is supported by the
National Pan Deng Project of China.
ttcher,
Dermer,
Carter-Lewis, Catanese, Ghisellini, Kataoka, and Wagner for their sending him
their publications and information and the Education fund
of Guangzhou City for support. This work is supported by the
National Pan Deng Project of China.


Up: The central black hole
Copyright The European Southern Observatory (ESO)
![]() -ray luminosity (assuming isotropic emission) and
Eddington-limit, one can derive the central black hole mass expression,
-ray luminosity (assuming isotropic emission) and
Eddington-limit, one can derive the central black hole mass expression,
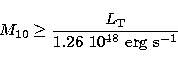
![\begin{displaymath}
M_{8}^{\rm KN} \geq {\frac{3\pi d_{\rm L}^{2}(m_{\rm e}c^{2}...
...},\varepsilon_{\rm u})}{1+z}}
\ln[2\varepsilon_{\rm l}(1+z)]
\end{displaymath}](/articles/aas/full/1999/07/ds7917/img54.gif)
![]() -ray flare, Hartman employed an accreting black hole of
-ray flare, Hartman employed an accreting black hole of
![]() , our result of
, our result of ![]() is similar to
theirs.
is similar to
theirs.
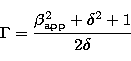
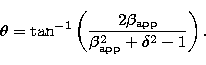
![]() ) be less than unity,
Doppler factor in
) be less than unity,
Doppler factor in ![]() -ray region has been obtained for some objects
by other authors.
-ray region has been obtained for some objects
by other authors.
![]() for Q1633+382 (Mattox et al. 1993);
for Q1633+382 (Mattox et al. 1993);
![]() for 3C 279 1996 flare (Wehrle et al. 1998) and
for 3C 279 1996 flare (Wehrle et al. 1998) and ![]() for
3C 279 1991 flare (Mattox et al. 1993),
for
3C 279 1991 flare (Mattox et al. 1993), ![]() is also
obtained by Henri et al. (1993);
is also
obtained by Henri et al. (1993);
![]() for
PKS 1622-297 (Mattox et al. 1997). Our results in Table 1 are consistent
with
those results.
for
PKS 1622-297 (Mattox et al. 1997). Our results in Table 1 are consistent
with
those results.
![]() ttcher,
Dermer,
Carter-Lewis, Catanese, Ghisellini, Kataoka, and Wagner for their sending him
their publications and information and the Education fund
of Guangzhou City for support. This work is supported by the
National Pan Deng Project of China.
ttcher,
Dermer,
Carter-Lewis, Catanese, Ghisellini, Kataoka, and Wagner for their sending him
their publications and information and the Education fund
of Guangzhou City for support. This work is supported by the
National Pan Deng Project of China.