For a King PSF, the asymptotic expression at high flux
of the count rate ![]() (Eq. 5)
of clean (not piled-up) monopixels,
can be written explicitly in the following way:
(Eq. 5)
of clean (not piled-up) monopixels,
can be written explicitly in the following way:
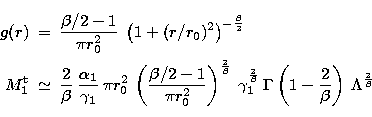 |
(B1) | |
| (B2) |
The expectation value of the total count rate M1 (Eq. 6) is somewhat more difficult to handle analytically but can also be written asymptotically in the following way:
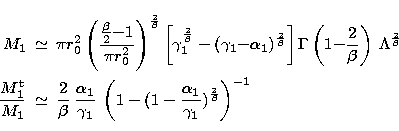 |
(B3) | |
| (B4) |
after splitting the integral in two, performing the same variable change
(with ![]() instead of
instead of ![]() for the first half),
integrating by parts the
for the first half),
integrating by parts the ![]() and
the
and
the ![]() terms
and noting that the two infinities at v = 0 cancel out exactly.
terms
and noting that the two infinities at v = 0 cancel out exactly.
This proves that for a PSF following a King profile the rates increase
at high flux as ![]() while the pile-up fraction
tends to a (small) constant. The transition to this regime
is when the incoming flux at the center gets higher than
while the pile-up fraction
tends to a (small) constant. The transition to this regime
is when the incoming flux at the center gets higher than ![]() of Eq. (4) and saturates.
of Eq. (4) and saturates.
For a Gaussian PSF (which has wings decreasing as fast as can be imagined for a reasonable PSF) the same kind of analytical exercise can be carried out:
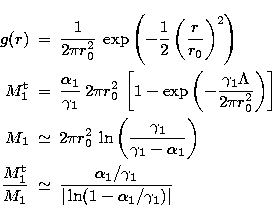 |
||
| (B5) | ||
| (B6) | ||
| (B7) |

Copyright The European Southern Observatory (ESO)