| |
(14) |
We performed four small simulation runs. Each time a beat period is covered
with a grid of equally spaced points and for each point (14) is
calculated, where the error term ![]() is generated from a
standard normal distribution. Then, we slide a window through the beat
period and for the set of observations within a window, a sinusoidal
approximation is calculated. From this approximation, the amplitude is retained.
From
these amplitudes,
is generated from a
standard normal distribution. Then, we slide a window through the beat
period and for the set of observations within a window, a sinusoidal
approximation is calculated. From this approximation, the amplitude is retained.
From
these amplitudes, ![]() and
and ![]() can be estimated and hence our proposed
expression for the standard deviation (13) can be computed. The
purpose of this study is to compare this with the "correct'' value, which is
determined as the sample standard deviation of
can be estimated and hence our proposed
expression for the standard deviation (13) can be computed. The
purpose of this study is to compare this with the "correct'' value, which is
determined as the sample standard deviation of ![]() in
(14). Rewrite
in
(14). Rewrite ![]() , where Pi is the period in
days. Apart from the parameters in
(14) we need to specify the number N of equally spaced times t
under consideration.
In addition, the number of replications n at each time needs to be
specified. The
settings are displayed in Table 1.
All phases are chosen
, where Pi is the period in
days. Apart from the parameters in
(14) we need to specify the number N of equally spaced times t
under consideration.
In addition, the number of replications n at each time needs to be
specified. The
settings are displayed in Table 1.
All phases are chosen
![]() .
.
In the first and the second simulation, there is only one pulsational mode and
therefore the observed amplitude is constant over time, implying that
![]() . The second simulation allows for a non-constant
. The second simulation allows for a non-constant ![]() which, for simplicity, is assumed to be of sinusoidal form as well. In order to
adequately cover the rapidly varying wave throughout the beat period, the
number of times N was increased by a factor 10. In both simulations, the true
standard deviation is about 7.14km s-1. We observe a relative error between
(13) and the true value smaller than 0.23% in the first simulation
and smaller than 0.15% in the second simulation. This confirms the correctness
of the formula (13).
which, for simplicity, is assumed to be of sinusoidal form as well. In order to
adequately cover the rapidly varying wave throughout the beat period, the
number of times N was increased by a factor 10. In both simulations, the true
standard deviation is about 7.14km s-1. We observe a relative error between
(13) and the true value smaller than 0.23% in the first simulation
and smaller than 0.15% in the second simulation. This confirms the correctness
of the formula (13).
The third simulation studies the particular case of two pulsational modes with
![]() ,
implying that
,
implying that
![]()
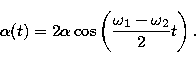 |
(15) |
In practice, formula (15) will not be available to determine the
statistical properties of the varying amplitude. Rather, it must be estimated
from a set of data. This is classically done using either Fourier transforms or
minimization in the least squares sense
(Bloomfield 1976) which is a special case of a statistical optimization method
known as profile likelihood (Welsh 1996). We used the second method in
the fourth simulation, which also enables us to cover the situation
![]() . Practically, we fitted a function
. Practically, we fitted a function
![]()
Copyright The European Southern Observatory (ESO)