

Up: An improved method for
Denote the radial velocity (RV) at time t, measured at wavelength 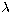 by
by
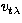 and the true underlying RV by vt. Further,
let
and the true underlying RV by vt. Further,
let 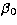 be the average RV. A two-stage statistical model is then
be the average RV. A two-stage statistical model is then
| 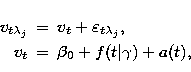 |
(1) |
| (2) |
(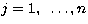 ),
where
),
where 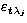 is a normally distributed error term with
variance
is a normally distributed error term with
variance 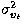 , due to
measurement error and wavelength calibration,
, due to
measurement error and wavelength calibration,
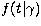 describes the orbital motion where
describes the orbital motion where 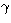 groups the orbital parameters,
and a(t) is a periodic
fluctuation of vt due to the pulsation of the star. A general
expression for a(t) is
groups the orbital parameters,
and a(t) is a periodic
fluctuation of vt due to the pulsation of the star. A general
expression for a(t) is
| 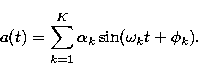 |
(3) |
Here, 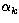 ,
, 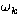 , and
, and 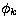 are the amplitude, the frequency,
and the phase of
the radial velocity due to the kth pulsation mode. It is assumed that the
frequency of
are the amplitude, the frequency,
and the phase of
the radial velocity due to the kth pulsation mode. It is assumed that the
frequency of 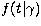 is much smaller than the pulsation frequencies
is much smaller than the pulsation frequencies
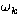 . This assumption ensures that it is reasonable to consider
. This assumption ensures that it is reasonable to consider
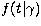 constant during a time period within which the sinusoidal terms
complete their cycles.
Clearly, Eqs. (1) and (2) can be combined into a single
one:
constant during a time period within which the sinusoidal terms
complete their cycles.
Clearly, Eqs. (1) and (2) can be combined into a single
one:
| 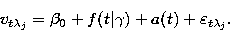 |
(4) |
When solely the estimation of vt for fixed t is of interest, it is
sufficient to obtain a number of replications at different wavelengths
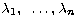 , whereafter they are averaged to yield
, whereafter they are averaged to yield
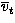 . The variance is equal to
. The variance is equal to
| 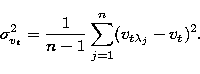 |
(5) |
Now, 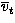 is an unbiased estimator for vt since the expectation
of
is an unbiased estimator for vt since the expectation
of 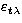 is assumed to be zero. Its standard deviation is
estimated by replacing vt in (5) with
is assumed to be zero. Its standard deviation is
estimated by replacing vt in (5) with 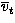 , and taking
the square root. In order to obtain the standard error we divide this
expression further by n.
, and taking
the square root. In order to obtain the standard error we divide this
expression further by n.
Moreover, 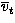 is
unbiased for the orbital motion
is
unbiased for the orbital motion 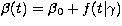 since in
addition a(t) is zero on average.
In contrast, the variance estimators are different in both situations since
since in
addition a(t) is zero on average.
In contrast, the variance estimators are different in both situations since
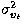 fails to acknowledge pulsational variability. Indeed,
fails to acknowledge pulsational variability. Indeed,
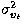 is the variance of
is the variance of 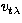 around vt, while we are
now interested in the spread of
around vt, while we are
now interested in the spread of 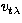 around
around 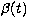 .
.
Since the pulsational variability and the error term
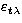 are statistically independent, Eq. (4)
yields
are statistically independent, Eq. (4)
yields
| ![\begin{eqnarray}
\sigma^2_{\beta(t)}&=&E[(v_{t\lambda}-\beta(t))^2]\\ &=&\mbox{v...
...&\mbox{var}[a(t)]+\frac{1}{n-1}\sum_{j=1}^n(v_{t\lambda_j}-v_t)^2.\end{eqnarray}](/articles/aas/full/1999/05/ds8135/img31.gif) |
(6) |
| |
| (7) |
| (8) |
When interest lies in the accuracy of the estimator 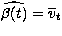 one should compute
one should compute
| ![\begin{eqnarray}
\mbox{var}
({\widehat{\beta(t)}})&=&E[(\overline{v}_{t}-\beta(t...
...
\right)\nonumber\\ &=&\mbox{var}[a(t)]+\frac{1}{n}\sigma^2_{v_t}.\end{eqnarray}](/articles/aas/full/1999/05/ds8135/img33.gif) |
|
| |
| (9) |
These variances will be used as weights for the determination of the unknown
orbital parameters.
Available data can consist of both full pulsation cycles as well as
measurements at a single time t (but at n different wavelengths
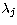 ). In the second case, the second term in (9) is
straightforward to evaluate but the first one is not. Indeed, even when we
can assume that
). In the second case, the second term in (9) is
straightforward to evaluate but the first one is not. Indeed, even when we
can assume that 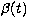 can be considered constant during a pulsation cycle,
a(t) is generally non-zero. Unfortunately, measurements at
a single t provide no information about the discrepancy between the two. In
order to overcome this problem, we will propose a method to determine the first
variance component from external information.
can be considered constant during a pulsation cycle,
a(t) is generally non-zero. Unfortunately, measurements at
a single t provide no information about the discrepancy between the two. In
order to overcome this problem, we will propose a method to determine the first
variance component from external information.
In the case of a monoperiodic pulsation, K=1 in (3).
When
more than one sine term is present, it is often reasonable to assume that the
function a(t) can be approximated by a single sine function during one night,
but that different approximations would be necessary for different nights. In
other words, we will assume that the sinusoidal amplitude 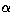 is constant
during one night, but fluctuates in a complicated fashion over longer periods
of time. To model this, we
assume that the amplitudes are drawn randomly from
a population of amplitudes with mean
is constant
during one night, but fluctuates in a complicated fashion over longer periods
of time. To model this, we
assume that the amplitudes are drawn randomly from
a population of amplitudes with mean 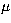 and variance
and variance 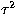 .This implies that, if several values for
.This implies that, if several values for 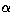 have been obtained,
have been obtained,
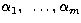 say, one can estimate the average
say, one can estimate the average 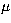 ,
,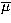 say, as well as the variance
say, as well as the variance
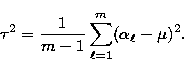
These results can be used to obtain the variance of a(t). Now, a(t) is a
sinusoidal function of t, however with variable amplitude 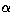 . To
account for this extra source of variation, we use a fundamental result
in mathematical statistics (Bickel & Doksum 1977, p. 36):
. To
account for this extra source of variation, we use a fundamental result
in mathematical statistics (Bickel & Doksum 1977, p. 36):
| ![\begin{displaymath}
\mbox{var}(a)=\mbox{var}[E(a\vert\alpha)]+E[\mbox{var}(a\vert\alpha)],\end{displaymath}](/articles/aas/full/1999/05/ds8135/img41.gif) |
(10) |
where 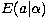 is the expectation of a(t), given a value of
is the expectation of a(t), given a value of 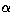 and
similarly
and
similarly
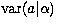 is the conditional variance of a
random variable. The unconditional counterparts are denoted by E(.) and
is the conditional variance of a
random variable. The unconditional counterparts are denoted by E(.) and
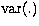 .
Now, assuming time t is uniformly distributed within a pulsation cycle
.
Now, assuming time t is uniformly distributed within a pulsation cycle
![$[0,2\pi/\omega]$](/articles/aas/full/1999/05/ds8135/img45.gif) , the conditional mean of a(t), given an amplitude
, the conditional mean of a(t), given an amplitude 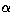 is
is
![\begin{displaymath}
E(a\vert\alpha)=
\frac{\omega}{2\pi}\int_0^{2\pi/\omega}\alpha\sin[\omega(t+\phi)]{\rm d}t=0\end{displaymath}](/articles/aas/full/1999/05/ds8135/img46.gif)
whence the first term in (10) cancels.
Secondly, the conditional variance of a(t), given an amplitude 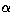 is
is
![\begin{displaymath}
\mbox{Var}(a\vert\alpha)=\frac{\omega}{2\pi}\int_0^{2\pi/\omega}
\alpha^2\sin^2[\omega(t+\phi)]{\rm d}t=
\frac{\alpha^2}{2}\end{displaymath}](/articles/aas/full/1999/05/ds8135/img47.gif)
of which the mean is
| ![\begin{eqnarray}
E[\mbox{var}(a\vert\alpha)]&=&E\left(\frac{\alpha^2}{2}\right)\...
...box{Var}(\alpha)\nonumber\\ &=&\frac{1}{2}\mu^2+\frac{1}{2}\tau^2.\end{eqnarray}](/articles/aas/full/1999/05/ds8135/img48.gif) |
|
| |
| (11) |
Substituting (11) into (10) leads to the following
variance formula for the estimated 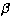 :
:
| 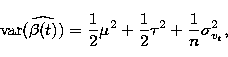 |
(12) |
which is estimated by plugging in estimated values for 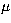 ,
, 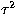 , and
, and
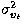 .
It is instructive to contrast
this quantity with the variance of a single measurement
.
It is instructive to contrast
this quantity with the variance of a single measurement
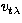 about the average RV
about the average RV 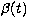 :
:
| 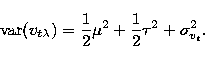 |
(13) |
When the number n of measurements 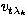 (
(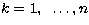 ) increases,
the determination of vt is done with increasing precision and the third term
in (12) approaches zero. In contrast, the intrinsic source of
uncertainty, due to the sinusoidal fluctuation, cannot be circumvented.
) increases,
the determination of vt is done with increasing precision and the third term
in (12) approaches zero. In contrast, the intrinsic source of
uncertainty, due to the sinusoidal fluctuation, cannot be circumvented.
Note that, for a star which is monoperiodic, K=1 and hence the same amplitude
will be found during each observational period. Hence, 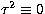 . In
practice, one might still find a small but non-zero value for
. In
practice, one might still find a small but non-zero value for 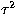 since
the amplitudes will be determined with measurement error.
since
the amplitudes will be determined with measurement error.


Up: An improved method for
Copyright The European Southern Observatory (ESO)
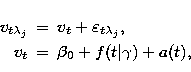
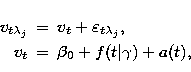
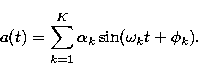
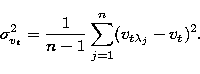
![]() is
unbiased for the orbital motion
is
unbiased for the orbital motion ![]() since in
addition a(t) is zero on average.
In contrast, the variance estimators are different in both situations since
since in
addition a(t) is zero on average.
In contrast, the variance estimators are different in both situations since
![]() fails to acknowledge pulsational variability. Indeed,
fails to acknowledge pulsational variability. Indeed,
![]() is the variance of
is the variance of ![]() around vt, while we are
now interested in the spread of
around vt, while we are
now interested in the spread of ![]() around
around ![]() .
.![]() are statistically independent, Eq. (4)
yields
are statistically independent, Eq. (4)
yields
![\begin{eqnarray}
\sigma^2_{\beta(t)}&=&E[(v_{t\lambda}-\beta(t))^2]\\ &=&\mbox{v...
...&\mbox{var}[a(t)]+\frac{1}{n-1}\sum_{j=1}^n(v_{t\lambda_j}-v_t)^2.\end{eqnarray}](/articles/aas/full/1999/05/ds8135/img31.gif)
![\begin{eqnarray}
\mbox{var}
({\widehat{\beta(t)}})&=&E[(\overline{v}_{t}-\beta(t...
...
\right)\nonumber\\ &=&\mbox{var}[a(t)]+\frac{1}{n}\sigma^2_{v_t}.\end{eqnarray}](/articles/aas/full/1999/05/ds8135/img33.gif)
![]() ). In the second case, the second term in (9) is
straightforward to evaluate but the first one is not. Indeed, even when we
can assume that
). In the second case, the second term in (9) is
straightforward to evaluate but the first one is not. Indeed, even when we
can assume that ![]() can be considered constant during a pulsation cycle,
a(t) is generally non-zero. Unfortunately, measurements at
a single t provide no information about the discrepancy between the two. In
order to overcome this problem, we will propose a method to determine the first
variance component from external information.
can be considered constant during a pulsation cycle,
a(t) is generally non-zero. Unfortunately, measurements at
a single t provide no information about the discrepancy between the two. In
order to overcome this problem, we will propose a method to determine the first
variance component from external information.
![]() is constant
during one night, but fluctuates in a complicated fashion over longer periods
of time. To model this, we
assume that the amplitudes are drawn randomly from
a population of amplitudes with mean
is constant
during one night, but fluctuates in a complicated fashion over longer periods
of time. To model this, we
assume that the amplitudes are drawn randomly from
a population of amplitudes with mean ![]() and variance
and variance ![]() .This implies that, if several values for
.This implies that, if several values for ![]() have been obtained,
have been obtained,
![]() say, one can estimate the average
say, one can estimate the average ![]() ,
,![]() say, as well as the variance
say, as well as the variance
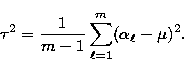
![\begin{displaymath}
E(a\vert\alpha)=
\frac{\omega}{2\pi}\int_0^{2\pi/\omega}\alpha\sin[\omega(t+\phi)]{\rm d}t=0\end{displaymath}](/articles/aas/full/1999/05/ds8135/img46.gif)
![\begin{displaymath}
\mbox{Var}(a\vert\alpha)=\frac{\omega}{2\pi}\int_0^{2\pi/\omega}
\alpha^2\sin^2[\omega(t+\phi)]{\rm d}t=
\frac{\alpha^2}{2}\end{displaymath}](/articles/aas/full/1999/05/ds8135/img47.gif)
![\begin{eqnarray}
E[\mbox{var}(a\vert\alpha)]&=&E\left(\frac{\alpha^2}{2}\right)\...
...box{Var}(\alpha)\nonumber\\ &=&\frac{1}{2}\mu^2+\frac{1}{2}\tau^2.\end{eqnarray}](/articles/aas/full/1999/05/ds8135/img48.gif)
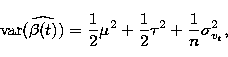
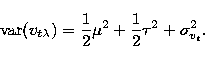
![]() . In
practice, one might still find a small but non-zero value for
. In
practice, one might still find a small but non-zero value for ![]() since
the amplitudes will be determined with measurement error.
since
the amplitudes will be determined with measurement error.