3 Calculation of level populations and emissivities

3.1 Calculation of b$_{n \ell}$

As in earlier calculations (HS and SH), we work in terms of the departure coefficients, $b_{n\ell}$, defined in terms of the Saha-Boltzmann populations at electron temperature $T_\mathrm{e}$ by  

$${{N_{n\ell}}\over{N_\mathrm{e} N_+}} = {{\omega_{n\ell}}\ove... ... mkT_\mathrm{e}}} \right)^{3/2} {\rm e}^{x_{n\ell}} b_{n\ell},$$ (3)

where $N_\mathrm{e}$ and N₊ are the number densities of electrons and recombining ions respectively, $x_{n \ell} = E_{n\ell}/kT_\mathrm{e}$, and $E_{n\ell}$ is the ionization energy of the state with quantum numbers $n,\ell$. The statistical weights of this state and of the ion ground state are $\omega_{n\ell}$ and $\omega_+$. A two stage process is used to compute the values of $b_{n\ell}$.

In the first stage, it is assumed that for a given n the states $n\ell$are populated in proportion to their statistical weight, so that $b_{n\ell}=b_n$for all $\ell$. This calculation is complete in the sense that a matrix condensation method is used to reduce the infinite set of algebraic equations determining the b_n to a finite set. All spontaneous radiative processes and electron induced collisional processes are included. The approximations used for these rates were given in HS.

In the second stage, the equations that determine $b_{n\ell}$ are solved by an iterative procedure. Above some limiting principal quantum number ($n=n_\mathrm{c}$), we assume that $b_{n\ell}=b_n$ and the values calculated in the first stage are used. For $n \leq n_\mathrm{c}$, the values of $b_{n\ell}$ are determined explicitly including the effects of $\ell$-changing collisions. The effect of collisions with electrons, protons and ionized helium atoms are included. For the calculation of the hydrogen spectrum, we assume that helium is singly ionized, whereas for the He II spectrum, we assume helium is doubly ionized. The helium abundance is taken to be 10% of that of hydrogen. An iterative solution for the $b_{n\ell}$ is carried out, starting at $n=n_\mathrm{c}$ and ending at n=2 with a maximum of twenty iterations being carried out. Above n=50, the values of $b_{n\ell}$ are interpolated as a function of n. This interpolation scheme and the approximations used for the required $\ell$-dependent rate coefficients are described in HS.

3.2 Calculation of emissivities for fine-structure components

The calculation of $b_{n\ell}$ described in Sect. 2.1 allows us to determine the emissivity in the hydrogenic transition $n_\mathrm{u} \ell_\mathrm{u} \rightarrow n_\mathrm{l} \ell_\mathrm{l}$; 

$$\varepsilon(n_\mathrm{u} \ell_\mathrm{u} \rightarrow n_\math... ...row n_\mathrm{l} \ell_\mathrm{l}) h\nu_{\mathrm{u}\mathrm{l}},$$ (4)

where A is a radiative transition probability and $h\nu_{\mathrm{u} \mathrm{l}}$ is the transition energy. The emissivity of a fine-structure component of this transition is

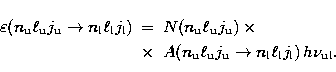$$\begin{eqnarray} \varepsilon (n_\mathrm{u} \ell_\mathrm{u} j_\mathrm{u} \righta... ...l} \ell_\mathrm{l} j_\mathrm{l}) \, h\nu_{\mathrm{u} \mathrm{l}}.\end{eqnarray}$$ (5)

In LS-coupling, the transition probabilities in Eqs. (4) and (5) are related by

$$\begin{eqnarray} A(n_\mathrm{u} \ell_\mathrm{u} j_\mathrm{u} \rightarrow n_\ma... ...thrm{u} \ell_\mathrm{u} \rightarrow n_\mathrm{l} \ell_\mathrm{l}),\end{eqnarray}$$ (6)

where { } is a 6-j symbol as defined for example by Brink & Satchler (1968). In this expression we have assumed that the fine-structure energy shifts are negligible compared to the transition energies. We further assume that $b_{n\ell j}=b_{n\ell}$, with the values of $b_{n\ell}$ being calculated as described above. This is equivalent to the assumption that the j-levels associated with a particular $n\ell$ are populated according to their statistical weights (2j+1).

Techniques for the rapid calculation of the values of $A(n_\mathrm{u} \ell_\mathrm{u} \rightarrow n_\mathrm{l} \ell_\mathrm{l})$ have been described by Storey & Hummer (1991).