For H I and He II energy levels we adopt the values given by Erickson (1977). These are based on quantum electrodynamic calculations including the Lamb shift. This work makes a careful comparison between experimental and calculated energy-level differences, and demonstrates good agreement. In general the theoretical QED uncertainty is smaller than the experimental error.
For each transition of H I and He II considered,
we adopted a reference wavelength, ![]() , for use as a
zero-point in the presentation of the shifts of individual component lines
in velocity space. These were computed from the Rydberg formula
, for use as a
zero-point in the presentation of the shifts of individual component lines
in velocity space. These were computed from the Rydberg formula
| |
(1) |
The difference in energy, ![]() , between the energy of a hydrogenic
state En, given by the Rydberg formula and the energy Enj obtained from
the Dirac equation is approximately
, between the energy of a hydrogenic
state En, given by the Rydberg formula and the energy Enj obtained from
the Dirac equation is approximately
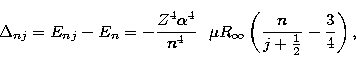 |
(2) |
We ignore hyperfine structure in this work. Its effect is to double
the energy levels of 1H and 3He, which have finite nuclear spin.
The typical splitting is
only ![]() , which corresponds to a velocity splitting
of
, which corresponds to a velocity splitting
of ![]() for optical and UV lines, and
is thus neglected.
for optical and UV lines, and
is thus neglected.
Table 1 lists, for some commonly observed transitions of H and He,
the number of components ![]() , the total range in velocity space
of the components
, the total range in velocity space
of the components ![]() , and the reference wavelength, defined as above,
for the four isotopes 1H, 2D, 3He and 4He.
We stress that the reference wavelength does not
represent any mean wavelength for the line in question, but is
simply a reference point to anchor our chosen scale of
velocity shifts.
Here, and throughout this paper, wavelengths are given in air for
, and the reference wavelength, defined as above,
for the four isotopes 1H, 2D, 3He and 4He.
We stress that the reference wavelength does not
represent any mean wavelength for the line in question, but is
simply a reference point to anchor our chosen scale of
velocity shifts.
Here, and throughout this paper, wavelengths are given in air for
![]() Å and in vacuum otherwise.
The variation of the velocity range of
the components as a function of nuclear mass (e.g. between
1H and 2H, or 3He and 4He) is too small to be recorded in
Table 1.
Å and in vacuum otherwise.
The variation of the velocity range of
the components as a function of nuclear mass (e.g. between
1H and 2H, or 3He and 4He) is too small to be recorded in
Table 1.
Copyright The European Southern Observatory (ESO)