

Up: First DENIS I-band extragalactic catalog
Subsections
A sample of 1146 objects has been visually classified into
three classes: stars, galaxies and unknown objects. The
distribution in each class is the following:
This sample will be used as a test sample (or training sample) in a
discriminant analysis method (DA) for galaxy recognition.
The DA is a common method for automatic recognition.
The test sample being shared in 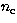 classes
classes 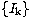 (k=1,
(k=1, 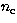 ), the purpose of DA is to find the principal factorial
axis on which each class is as concentrated as possible
and as distinct as possible from the others. This is achieved by maximizing
the inertia between classes and by minimizing the inertia within each class.
Inertia is calculated from the set of parameters attached to each object.
We will note pij the j-th parameter of object i.
), the purpose of DA is to find the principal factorial
axis on which each class is as concentrated as possible
and as distinct as possible from the others. This is achieved by maximizing
the inertia between classes and by minimizing the inertia within each class.
Inertia is calculated from the set of parameters attached to each object.
We will note pij the j-th parameter of object i.
The mathematical result (see Diday et al. 1982) is that the factorial axes
are the eigenvectors of the matrix 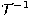 .
. 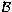 , where
, where
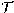 is the total covariance matrix and
is the total covariance matrix and 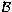 is the
inter-class covariance matrix.
is the
inter-class covariance matrix.
Note that the matrix 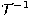 .
. 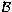 is not symmetrical and that
the total covariance matrix is the sum of
the intra-class covariance matrix
is not symmetrical and that
the total covariance matrix is the sum of
the intra-class covariance matrix 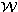 (covariance Within class)
and of inter-class covariance matrix
(covariance Within class)
and of inter-class covariance matrix 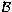 (covariance Between class).
This is called the Huyghens decomposition.
(covariance Between class).
This is called the Huyghens decomposition.
| 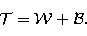 |
(1) |
The elements of 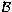 are:
are:
| 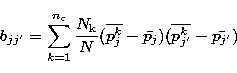 |
(2) |
where Nk is the number of objects in the class Ik (k=1 to
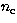 ), where the mean parameter j for the whole sample is:
), where the mean parameter j for the whole sample is:
| 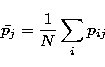 |
(3) |
(N is the number of objects of the whole sample), and where the mean
parameter j within the class 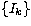 is:
is:
| 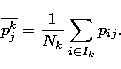 |
(4) |
The elements of the total covariance matrix 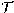 are:
are:
| 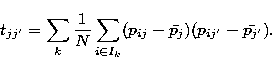 |
(5) |
Now, we have to choose the set of parameters attached to each object.
Any discriminant method requires a good choice of discriminant
parameters which are used for the definition of the metric.
These parameters are not necessarily independent but they must
cover all features which seem relevant for a reliable discrimination of
astronomical objects. For galaxy recognition we tested 7 parameters.
- 1.
- Peak intensity per area unit, this is Peak intensity divided by the
surface of the considered object.
- 2.
- Mean surface brightness, total flux divided by area.
- 3.
- Peak intensity.
- 4.
- Axis ratio, ratio of the major to the minor axis.
- 5.
- Relative area, ratio of number of pixels of the object and of the matrix.
- 6.
- Elongation of the matrix.
- 7.
- Presence of diffraction cross.
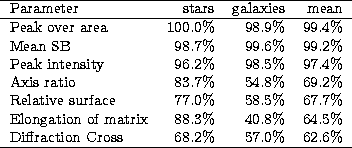
The DA method is applied on half the sample (i.e. 573 objects) and
tested on the other half using only one parameter at a time (in this case
the factorial axis is defined by the parameter itself).
The percentage of good results is given below for
each one, individually.
The conclusion of this test is that the most relevant information about
the nature of an object is contained in the pixel intensity, not in the shape of the object.
Stars have a very high central intensity, galaxies do not. Moreover, stars
are concentrated, galaxies are not.
This explains why "Mean SB'' and "Peak over area'' give such an impressive recognition rate.
Finally, only the first four parameters have been used.
The axis ratio is kept because it becomes relevant for faint objects despite
that its rate is relatively low.
The DA method is applied with the four parameters described above and three
classes "Galaxies'', "Stars'' and "unknown objects''.
Using the test sample, each object
is projected onto the first factorial axis. Figure 5 shows
the projection onto the first factorial axis of "Galaxies'' and
"Stars'' classes. Similar plots exists for "Stars'' and "unknown
objects'' classes and for "Galaxies'' and "unknown objects''
classes. All "unknown
objects'' have been eliminated in the next part of this study.
One can see that there is an overlapping region where "Galaxies''
and "Stars'' are mixed. The limits of this zone can be tuned in such
a way that one can accept a given percentage of misclassification. We choose
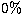 chance of classifying a star as a galaxy and
chance of classifying a star as a galaxy and 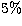 chance of classifying
a galaxy as a star. Indeed, it is important to avoid the contamination
of the catalog by stars while it is not as important to miss a galaxy (which
is uncertain anyway). These limits are drawn in Fig. 5 where it
is visible that no star enter the galaxy-domain, while
chance of classifying
a galaxy as a star. Indeed, it is important to avoid the contamination
of the catalog by stars while it is not as important to miss a galaxy (which
is uncertain anyway). These limits are drawn in Fig. 5 where it
is visible that no star enter the galaxy-domain, while 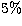 of galaxies
enter the star-domain. Objects between these two limits will be classified
as undefined.
of galaxies
enter the star-domain. Objects between these two limits will be classified
as undefined.
![\begin{figure}
\includegraphics [width=8cm]{ds8041f6.eps}\end{figure}](/articles/aas/full/1999/04/ds8041/Timg43.gif) |
Figure 5:
Definition of acceptation zones along the first factorial axis.
The left-hand zone defines "Galaxies'', the righthand one defines "Stars'',
and the intermediate one defines "undefined objects'' |
The final step of this treatment consists in checking visually all frames
recognized as galaxies. This tedious part allows us to reject artefacts
(1148 rejections after the inspection of 54073 images)
like those produced by star halos truncated by the edge of the frame.
Such truncated halos look like elongated, low-surface brightness object,
easily accepted as galaxies.
As a result, a code is given to describe three features:
- "multiple'', if several objects are present in the matrix
- "truncated'', if the galaxy is truncated by the edge of the array.
- "peculiar'', if the galaxy looks strange for any reason.
So, each galaxy of the catalog has been inspected visually. This will prevent
us from gross misidentification.
Now, the galaxies have to be cross-identified with known galaxies.


Up: First DENIS I-band extragalactic catalog
Copyright The European Southern Observatory (ESO)


![]() .
. ![]() , where
, where
![]() is the total covariance matrix and
is the total covariance matrix and ![]() is the
inter-class covariance matrix.
is the
inter-class covariance matrix.
![]() .
. ![]() is not symmetrical and that
the total covariance matrix is the sum of
the intra-class covariance matrix
is not symmetrical and that
the total covariance matrix is the sum of
the intra-class covariance matrix ![]() (covariance Within class)
and of inter-class covariance matrix
(covariance Within class)
and of inter-class covariance matrix ![]() (covariance Between class).
This is called the Huyghens decomposition.
(covariance Between class).
This is called the Huyghens decomposition.
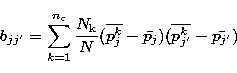
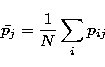
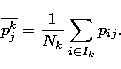
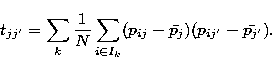
![]() chance of classifying a star as a galaxy and
chance of classifying a star as a galaxy and ![]() chance of classifying
a galaxy as a star. Indeed, it is important to avoid the contamination
of the catalog by stars while it is not as important to miss a galaxy (which
is uncertain anyway). These limits are drawn in Fig. 5 where it
is visible that no star enter the galaxy-domain, while
chance of classifying
a galaxy as a star. Indeed, it is important to avoid the contamination
of the catalog by stars while it is not as important to miss a galaxy (which
is uncertain anyway). These limits are drawn in Fig. 5 where it
is visible that no star enter the galaxy-domain, while ![]() of galaxies
enter the star-domain. Objects between these two limits will be classified
as undefined.
of galaxies
enter the star-domain. Objects between these two limits will be classified
as undefined.