Our series, called REN2000 (REN for Rigid Earth Nutation) are ready and available at this level of truncation. They give the nutation for the axis of angular-momentum, the axis of figure and the axis of rotation, in separate files. The basic plane of reference and the basic point of reference are respectively the mean dynamical ecliptic and the mean equinox of the date. Hamiltonian theory is very well suited to give the nutations with respect to a moving point (equinox of the date) and a moving plane (the mean dynamical ecliptic), for the change of canonical variables caused by their motions with respect to the fixed ecliptic and the fix equinox of the epoch is quite straightforward (Kinoshita 1977).

**Table 4:** The largest Oppolzer terms (figure axis - ang. momentum axis) in rigid Earth nutation; the symbol "C" indicates that the coefficients is the combination of two contributions (lunar+solar)
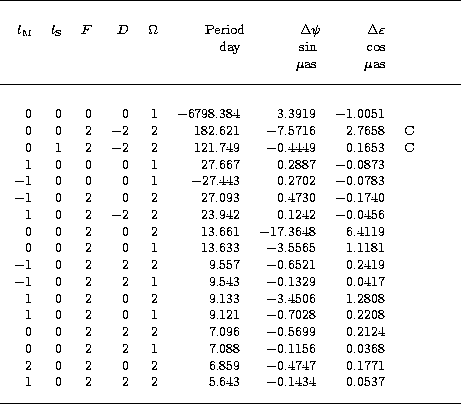
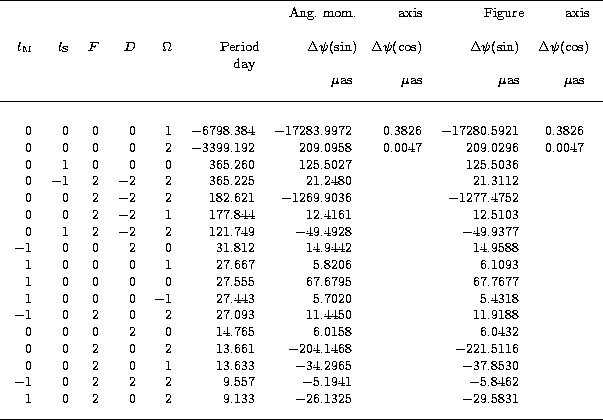
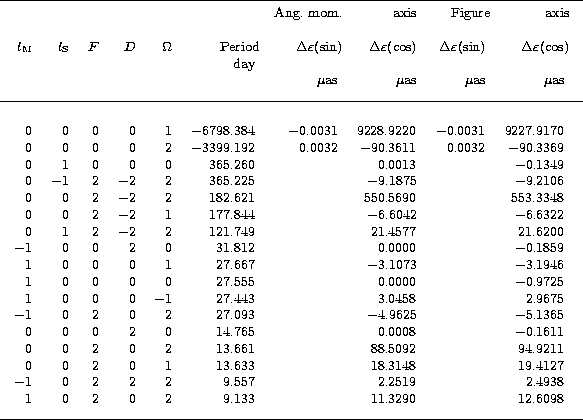
$\begin{table} \begin{displaymath} \vbox{ \halign{ ...$

In Table 4, we present the largest Oppolzer terms which characterize the difference between the nutations for the figure axis and for the angular momentum axis, and in Tables 5.1 and 5.2 we give the values of the leading coefficients of rigid Earth nutation for the angular momentum axis and the figure axis, both in longitude and in obliquity. Little changes can be remarked with respect to the values listed by Souchay & Kinoshita (1996). They are due to the improved second-order computations related to the crossed-nutation effect and the coupling effect as described in the precedent chapters and illustrated by Tables 1 and 2.

**Table 5:** 1. The largest components of rigid Earth nutation, longitude part, angular momentum axis and figure axis, for epoch J2000.0. When some coefficients are the combination of a lunar and solar contribution, they are mixed together
$\begin{table} \begin{displaymath} \vbox{ \halign{ ...$

**Table 5:** 2. The largest components of rigid Earth nutation, obliquity part, angular momentum axis and figure axis, for epoch J2000.0. when some coefficients are the combination of a lunar and a solar contribution, they are mixed together
$\begin{table} \begin{displaymath} \vbox{ \halign{ ...$

Our tables REN-2000 include also the semi-diurnal coefficients related to the triaxiality of the Earth (Souchay & Kinoshita 1997), as well as the diurnal, semi-diurnal and 1/3 d period nutations related to the tesseral harmonics C_3,n and S_3,n, (n=1,2,3). These last ones were studied in a complementary paper by Folgueira et al. (1998a), by taking the same Hamiltonian method as in the present paper. Notice that the amplitude of these waves reaches $40 ~\rm \mu as$ as was already noticed by Bretagnon et al. (1997). The waves related to the tesseral harmonics C⁴_m,n and S⁴_m,n (Folgueira et al. 1998b) are also taken into account, as well as the two waves up to our level of truncation ( $0.1 ~\rm\mu as$ ) for the influence of J₄ (Souchay & Kinoshita 1996).

**Table 6:** Number of coefficients larger than 0.1 $\mu {\rm as}$ included in the tables REN-2000, according to their origin
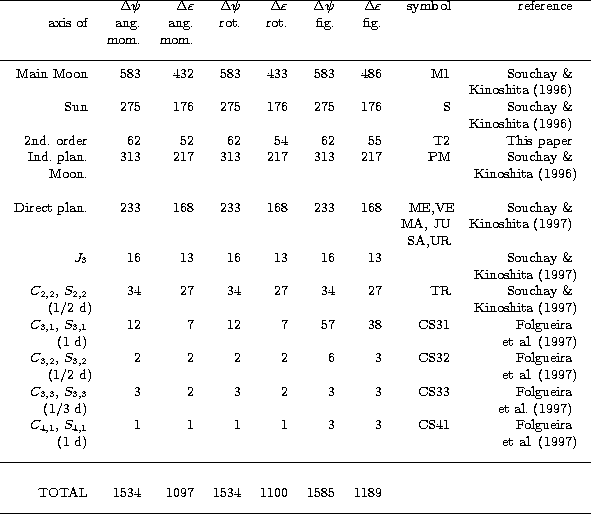$\begin{table} \begin{displaymath} \vbox{ \halign{ ...$

In order to have a clear insight of various contributions to the rigid Earth nutation, we list in Table 6 the number of coefficients related to each specific effect, up to $0.1 ~\rm\mu as$ . The symbol used in the tables in order to reckon the effect involved, is indicated here. At last, the bibliographic reference from which the coefficients of our tables REN-2000 have been picked up is also given for each specific effect. For a better understanding of the presentation of our tables REN-2000, we give in the following some comments and remarks that we would like to present, with respect to each contribution.

The major contribution to the nutation, as considering the importance of the effect and of the number of coefficients, comes from the Main Problem of the Moon, that is to say from its orbital motion when being disturbed only by the Sun. It is worthy to notice that the arguments of the terms coming from this effect are expressed in function of the only Delaunay arguments F, D, $l_{\rm M}$ , $l_{\rm S}$ and $\Omega$ (Chapront-Touzé & Chapront 1988). The related nutation has been calculated with up-to-date analytical Fourier series of Moon coordinates taken in the recent version of ELP-2000 (Chapront-Touzé & Chapront 1988), with a truncature at a relative 10^-11 for all the Fourier series concerned in the calculations in order to avoid cut-off problems (Souchay & Kinoshita 1996). The Moon's coordinates in ELP2000 are given with respect to the moving ecliptic and equinox of the date, which constitute a precious advantage for our theory is itself established starting from the moving ecliptic and equinox. Therefore we have not further coordinates transformations to carry out, as it would be the case if our basic equations were given in an inertial frame. Concerning the nutation due to the main problem of the Moon at the first-order, we find no significant difference with older calculations (Kinoshita & Souchay 1990), except for the contribution coming from the planetary tilt effect described in detail and calculated by Williams (1994) and recalculated by Souchay & Kinoshita (1996), and which only influences the coefficient with argument $\Omega$ and $2 \Omega$ . Notice that the number of terms is the same for the three axe in $\Delta \psi$ . On the other hand, the number of terms for $\Delta \varepsilon$ is noticeably larger for the figure axis than for the angular momentum axis (486 instead of 432). This is due to the fact that the terms in the potential with argument not containing $\Omega$ can give birth to a nutation component in obliquity only for the figure axis, and not the axis of angular momentum.

These terms are coming from the perturbations exerted by the planets on the orbital motion of the Moon, and consequently on the nutation as computed from the lunar potential. Their argument is systematically expressed in function of the Delaunay's ones (F, D, $l_{\rm M}$ , $l_{\rm S}$ and $\Omega$ ) and a combination of the mean longitudes of the planets expressed with respect to the fixed equinox and ecliptic of the epoch J2000.0. Notice that the coefficients larger than $5 ~\rm\mu as$ resulting from our recalculations have been listed by Souchay & Kinoshita (1996), with some corrections with respect to previous tables (Kinoshita & Souchay 1990). In order to have a qualitative idea of the effect studied here, we show in Figs. 1.1 and 1.2, respectively for a 2 years time span and a 180 years time span, the curve of the indirect planetary effects on the nutations due to the Moon. At high frequencies this curve is dominated by two terms with periods 13.659 d and 13.663 d respective arguments $-l_{\rm M} + 2F + 2 \Omega +18 \lambda_{\rm Ve} - 16 \lambda_{\rm Ea}$ and $l_{\rm M} + 2F + 2 \Omega -18 \lambda_{\rm Ve} + 16 \lambda_{\rm Ea}$ and the same amplitude

$14.1 ~\rm\mu as$ . At low frequency the peak-to-peak amplitude reaches 1 $\mu$ as in a little more than 100 years. Similar observations can be done for the nutation in obliquity.

$\begin{figure} \includegraphics []{7187f1.eps}\end{figure}$

Figure 1: Indirect planetary effect on the nutation $\Delta \psi$ exerted by the Moon, for a 180 years time span (Fig. 1.1) and a 2 yearts time span (Fig. 1.2)

The contribution of the Sun to the nutation, calculated from VSOP series (Bretagnon & Francou 1988) for the orbital elements of the Earth is characterized by two different kinds of terms: some of them (15 terms for $\Delta \psi$ and 8 for $\Delta \varepsilon$ ) are expressed as a function of the Delaunay arguments only, as the leading component of argument $2 L_{\rm S} = 2F - 2D + 2\Omega$ . The others are expressed as a function of the Delaunay's arguments and of the mean longitudes of the planets. These last terms which are quite numerous (260 terms for $\Delta \psi$ and 168 for $\Delta \varepsilon$ ) are sometimes quoted as indirect planetary effect, but we can observe that this appellation, although being adopted, looks a little wrong, for the planets themselves have some influence in the value of the first category of terms, which are therefore not the product of a simple two-bodies problem.

Only a few significant differences are found for the terms already taken into account previously (Kinoshita & Souchay 1990), despite the new high order of relative truncation of the coefficients (10^-11). Souchay & Kinoshita (1996) made the necessary corrections, essentially due to the new value of the general precession in longitude with respect to the IAU conventional value (Lieske et al. 1977), but also to several erroneous values in the tables of Kinoshita & Souchay (1990) as was pointed out by Williams (private communication). Notice that some of the corrections, reaching roughly the value of $4 ~\rm\mu as$ , originate from the fact that the latitude of the Sun with respect to the moving ecliptic of the date is not rigorously equal to zero (Souchay & Kinoshita 1996). We show for $\Delta \psi$ the indirect planetary effect due to the Sun (following the somewhat improper appellation as explained above), for a short time span (2 years), respectively in Fig. 2.1 and for a long one (100 years) in Fig. 2.2. Notice that the aspect of the curve is quite different than in the case of the Moon (Figs. 1.1 and 1.2) for no significant term is present at less than the half-year period. By contrast the combination of numerous contributing coefficients between 0.5 y and 10 years leads to a very disturbed curve at the scale of one year.

$\begin{figure} \includegraphics []{7187f2.eps}\end{figure}$

Figure 2: Indirect planetary effect on the nutation $\Delta \psi$ exerted by the Sun, for a 180 years time span (Fig. 2.1) and a 2 years time span (Fig. 2.2)

We call second-order components those which involve a second-order effect, but it must be emphasized that in the general case they are the combination of this second-order effect and a first-order contribution, which is often much more larger. The leading 18.6 y coefficient is then for instance ranged into this category. The second-order effects can be divided into two independent parts (orbital coupling and crossed-nutation) which have been studied in detail in the preceding sections. Because of the new truncation limit the number of components undergoing second-order modifications has considerably increased with respect to previous results: 62 terms in $\Delta \psi$ and 52 terms in $\Delta \varepsilon$ compared with only 7 terms both in $\Delta \psi$ and $\Delta \varepsilon$ found by Kinoshita & Souchay (1990). Nevertheless the truncation limit is not the only explanation: some new coefficients are found here but not in this last paper, although their amplitude was up to the old level of truncation, that is to say $5 ~\rm\mu as$ . The reason must be found in the completion of the present calculations. Notice also that crossed-nutation terms can come from the interaction of one nutation component originating in the potential exerted by the Moon and one nutation component originating in the potential exerted by the Sun. In an opposite side, the Sun does not contribute at all to spin-orbit coupling.

This effect has been computed recently at the $0.1 ~\rm\mu as$ level both by Williams (1995) and Souchay & Kinoshita (1997). As it is shown in tables from this last paper, the agreement between the two works is quasi-perfect, despite the fact that the way of calculations is different. For the great majority of coefficients, there is no difference in the amplitude, at the level of truncation above ( $0.1 ~\rm\mu as$ ). Notice that even the influence of Mercury and Uranus has to be taken into account. The major contribution comes from Venus, Mars and Jupiter. Venus itself contributes to 147 coefficients in $\Delta \psi$ , that is much more than all the other planets together. The reason must be found both in its proximity to the Earth and therefore in the big number of significant terms in the potential having as argument the combination of the mean longitudes of the two planets (the Earth and Venus). Here also the computations have been done with a relative 10^-11 truncation of intermediate series. The terms of nutation related to the direct planetary effect in our tables REN-2000 can be easily reckoned by the fact that their arguments is only a fuction of the mean longitudes of the planets. In other words, they are the only terms for which the Delaunay arguments ( $l_{\rm M}, l_{\rm S}, F, D, \Omega$ )are not present.

The second-order potential J₃ of the Earth gives birth to 17 coefficients in longitude and in obliquity up to $0.1 ~\rm\mu as$ as was listed by Souchay & Kinoshita (1997). It is characterized by a very large set of frequencies, the smallest period (argument $l_{\rm M} + 3F + 3 \Omega$ ) being 6.8 d, and the largest one (argument $-l_{\rm S} + F - D + \Omega$ ) being 20935 y. The leading coefficient is closed to 0.1 $\mu$ as both in longitude and in obliquity, and has a 8.85 y period, with argument $-l_{\rm M}+F+\Omega$ . Here also the comparison with Hartmann et al. (1995) is quasi-perfect for the biggest difference in amplitude is $0.6 ~\rm\mu as$ , and is less than $0.1 ~\rm\mu as$ for 15 coefficients among the 20 coefficients which have been recognized by these last authors (for their level of truncature is larger).

The coefficients of the geopotential C_2,2 and S_2,2 which are characterizing the triaxiality of the Earth, naturally lead to the presence of coefficients of nutation with quasi semi-diurnal period, and their joint effect leads to a beating (Souchay 1993) dominated by 3 coefficients at periods 0.518 d, 0.500 d and 0.499 d, with respective arguments $2 \Phi - 2F -2 \Omega$ , $2 \Phi - 2F + 2D -2 \Omega$ and $2 \Phi$ , and respective amplitudes $27.1 ~\rm\mu as$ , $12.5 ~\rm\mu as$ and $-37.8 ~\rm\mu as$ in longitude, $11.0 ~\rm\mu as$ , $4.7 ~\rm\mu as$ and $15.0 ~\rm\mu as$ in obliquity. Notice that the largest coefficient originates from both the influence of the Sun and the influence of the Moon. Two points must be emphasized: at first the angle $\Phi$ is not the angle of the sidereal rotation of the Earth, for it is shifted by a phase which corresponds to the longitude difference between the prime meridian and the axis of minimum moment of inertia (Bretagnon et al. 1997), which amounts roughly to $15^{\circ}$ . This point is detailed in the next chapter. Secondly the coefficients of nutation coming from this effect as they were listed by Kinoshita & Souchay (1990) up to $5 ~\rm\mu as$ and by Souchay & Kinoshita (1997), up to $0.1 ~\rm\mu as$ correspond to the axis of angular momentum. By their semi-diurnal periodic properties, the respective nutation terms for the figure axis have the opposite sign and a very close amplitude (at the present level of truncation), as can be shown from straightforward relationships (Kinoshita 1977).

Thus it can be easily shown that for a given coefficient of the nutation of the angular momentum axis due to the triaxiality, with amplitude $(\Delta \psi_{\rm A.M.})$ and period P in days ( $P \approx 0.5$ d), the respective coefficient of nutation will be:

$\begin{displaymath} (\Delta \psi)_{\rm fig.} = - (\Delta \psi)_{\rm A.M.} + \lef... ...s \left( {P_{\rm g} - 2 P \over P_{\rm g} - P}\right) \right] \end{displaymath}$

(50)

where $P_{\rm g}$ is the period of the canonical variable g which represents the angle between the intersection of the plane $\Sigma_{\rm am}$ perpendicular to the angular momentum vector with the ecliptic of the date, and the intersection between $\Sigma_{\rm am}$ and the equator of figure (Kinoshita 1977). The numerical value for $P_{\rm g}$ being: $P_{\rm g} \approx 0.997$ d, we can observe that the second term at the right-hand side of (50) is small in comparison to the first one, and then that the amplitude for $(\Delta \psi)_{\rm fig}$ is close to that of $(\Delta \psi)_{\rm A.M.}$ with the opposite sign. The more P is close to $P_{\rm g}/2$ , the more the absolute values of these amplitudes become relatively closer one to each other, for the second term is gradually vanishing.

**Table 7:** 1. The largest terms of rigid Earth nutation with period P $\leq 2$ d, longitude part, both for the angular momentum axis and the figure axis
$\begin{table} \begin{displaymath} \vbox{ \halign{ ...$

**Table 7:** 2. The largest terms of rigid Earth nutation with period P $\leq 2~d$ , obliquity part, both for the angular momentum axis and the figure axis
$\begin{table} \begin{displaymath} \vbox{ \halign{ ...$

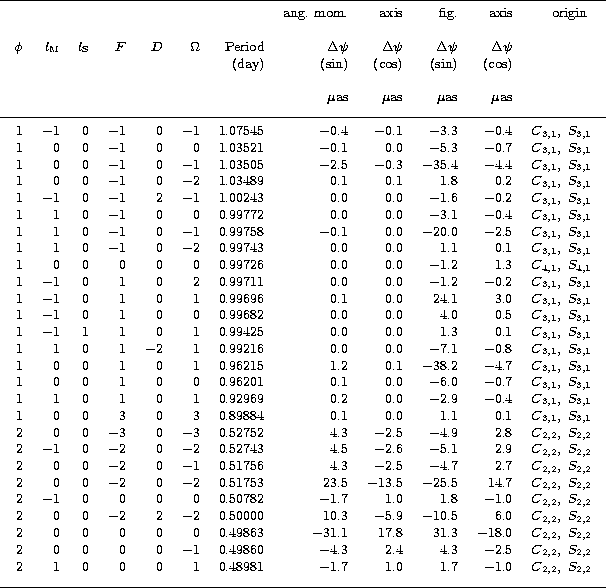
So it seems necessary to remind of this property, in order to avoid any misunderstanding concerning the tables, where the opposite sign between the values for the angular momentum axis and those for the figure axis, might be interpreted as an error. In Table 7.1, all the coefficients of rigid-Earth nutation in $\Delta \psi$ up to $1 ~\rm \mu as$ due to the triaxiality of the Earth, marked by the symbol CS22, have been gathered together with the coefficients coming from the C_3,i and S_3,i geopotential, which will be studied in the next section. C_3,2 and S_3,2 give also birth to quasi semi-diurnal components of nutation, which do not reach the $1 ~\rm \mu as$ level. Table 7.2 is the table corresponding to Table 7.1, in obliquity.

The terms of nutation related to the geopotential harmonics C_3,i and S_3,i have been computed for the first time recently, by Bretagnon et al. (1997), and can be ranged into three categories: the quasi-diurnal terms, which originate from C_3,1 and S_3,1, the quasi semi-diurnal terms, which originate from C_3,2 and S_3,2, and at last the quasi 1/3 d periodic terms, which originate from C_3,3 and S_3,3. One of the specific properties of the diurnal terms is that the amplitudes of the angular momentum components is much smaller than the amplitude of the component which is the figure axis counterpart. In other words, the Oppolzer terms are themselves much bigger than the amplitude of the nutation of the angular momentum, which is not the case of all the other nutations, for which it is by one or two orders smaller, when non negligible (except the contribution of C_2,2 and S_2,2, for which the order is the same). Folgueira et al. (1998a) calculated the contribution of the C_3,i's and S_3,i's with the help of Hamiltonian canonical equations, following the same way of calculation as Kinoshita (1977). It can be seen from these calculations that the relatively large amplitude of Oppolzer terms comes from the fact that some components in the determining function W do not contain the variable g at the denominator (g has a nearly diurnal period), so that they keep on remaining big after integration. Here also the agreement for the three kinds of contribution is very good between the results found and Bretagnon et al. (1997), as is shown in a comparative table (Souchay 1997). Notice that the largest diurnal component has an amplitude of $38.5 ~\rm\mu as$ in longitude and $15.2 ~\rm\mu as$ in obliquity, with respective arguments $\Phi - F - \Omega - \tau_{3,1}$ where: $\tau_{3,1} = - S_{3,1} / C_{3,1}$ . The characterization of the angle $\Phi$ will be given in the chapter 6. Concerning the contribution studied here, the tables in REN-2000 are the same as in Folgueira et al. (1998a) when the phases $\tau_{3,i}, (i=1,3)$ have been replaced in each argument by their numerical value so that the nutation terms are split into sine and cosine components. In Tables 7.1 and 7.2, we show the largest of the nutations from C_3,1 and S_3,1, respectively in longitude and in obliquity, indicated by the symbol CS31.

They have been computed by Bretagnon et al. (1997) and by Folgueira et al. (1998b). The coefficients retained in the tables REN-2000 are coming from this last paper. Only 5 components are larger than $0.1 ~\rm\mu as$ (3 for $\Delta \psi$ and 2 for $\Delta \varepsilon$ ). The leading one can be written, in $\rm\mu as$ : $\Delta \psi = 1.4 \sin \Phi -1.2 \cos \Phi$ , and: $\Delta \varepsilon = 0.4 \cos \Phi + 0.5 \sin \Phi$ For these terms also the amplitude of the coefficients is much bigger for the figure axis than for the axis of angular momentum.

**Table 8:** Parameters and constant terms used for the construction and the use of the series REN-2000
$\begin{table} \begin{displaymath} \vbox{ \halign{ ...$

5 Final tables of nutation REN-2000