The computation of the 18.6 y leading coefficients of nutation, both in longitude and in obliquity, is rather delicate, so that this chapter is devoted to it. As explained in detail by Williams (1994) and Souchay & Kinoshita (1996), these coefficients are the result of the combination of various contributions, which are, for the in-phase coefficient: the first-order component related to the main problem of the Moon, the crossed-nutation effect, the spin-orbit coupling effect, the planetary- tilt effect.
For the out-of-phase components, contributions come from the planetary-tilt
effect (Williams 1994) and from the secular variation of the mean obliquity with respect
to the moving ecliptic of the date. This last contribution, clearly pointed out and
accurately calulated recently by Bretagnon et al. (1997), was not considered in previous
works (Kinoshita & Souchay 1990) although already
Kinoshita (1977) mentioned that strictly
speaking, in the integration of the potential which serves to give the expression
of the determining function in Hamiltonian theory, we shoud have to take into account the
secular change of the obliquity ![]() (which is the value of the obliquity when
not considering its periodical variations, that is to say the mean obliquity itself
including its secular variation). By taking into account this effect, we find a
correction for the out-of-phase coefficient in longitude of which matches very well the
difference found by Bretagnon et al. (1997) when comparing his value with
Souchay
& Kinoshita (1997), that is to say 0.250
(which is the value of the obliquity when
not considering its periodical variations, that is to say the mean obliquity itself
including its secular variation). By taking into account this effect, we find a
correction for the out-of-phase coefficient in longitude of which matches very well the
difference found by Bretagnon et al. (1997) when comparing his value with
Souchay
& Kinoshita (1997), that is to say 0.250 ![]() as.
as.
The calculation related to the correction above consists in
replacing the constant value of ![]() at J2000.0 in the expression
of the potential by
at J2000.0 in the expression
of the potential by ![]() where
where ![]() is the secular variation of the
mean obliquity of the date (
is the secular variation of the
mean obliquity of the date (![]() ) with respect to the mean ecliptic of the
date.
The conventional value of
) with respect to the mean ecliptic of the
date.
The conventional value of ![]() can be found in Lieske et al. (1977), that is
to say:
can be found in Lieske et al. (1977), that is
to say: ![]() 1000 yrs. = 0.0022696 rd /1000 yrs. Then after integrating
the potential and applying the canonical equations which serve to the determination of
the coefficients of nutation at the first order (Kinoshita 1977), we find that the ratio of
the out-of-phase
1000 yrs. = 0.0022696 rd /1000 yrs. Then after integrating
the potential and applying the canonical equations which serve to the determination of
the coefficients of nutation at the first order (Kinoshita 1977), we find that the ratio of
the out-of-phase ![]() component with respect to the in-phase one is
component with respect to the in-phase one is
![]() in longitude, and:
in longitude, and: ![]() in obliquity.
in obliquity.
Thus the values in milliarcsecond obtained for the out-of-phase component are
![]() for
for ![]() and
and ![]() for
for
![]() . Notice that these values are the same as those found
Roosbeek &
Dehant (1997).
. Notice that these values are the same as those found
Roosbeek &
Dehant (1997).
Moreover, in longitude only, the secular variation of the obliquity produces an additional out-of-phase component coming from the expression of the complementary part of the Hamiltonian E (Kinoshita 1977) which is related to the change of canonical variables from the fixed ecliptic of the epoch to the moving ecliptic of the date. E can be written, by using the same notations as in Kinoshita (1977):
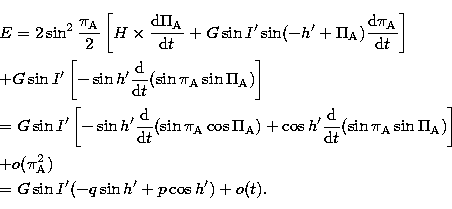 |
||
| (45) |
Where h' is the combination of the general precession in
longitude ![]() ) and of the nutation in longitude:
) and of the nutation in longitude:
![]() .By applying the canonical equations:
.By applying the canonical equations:
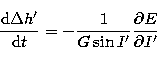 |
(46.1) |
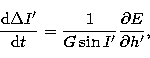 |
(46.2) |
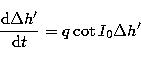 |
(47.1) |
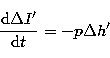 |
(47.2) |
By taking: ![]() J cy. and p = 5.341''/J cy.
integration of equations (47.1) and (47.2) leads to the following
values:
J cy. and p = 5.341''/J cy.
integration of equations (47.1) and (47.2) leads to the following
values:
![]()
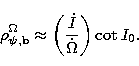 |
(48) |
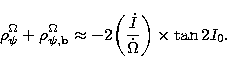 |
(49) |
Notice that the second-order tilt-effect (Souchay & Kinoshita 1996) gives
0.1351 ![]() as and
as and ![]() as for the out-of-phase part respectively for
as for the out-of-phase part respectively for
![]() and
and ![]() , so that the final values
are respectively 0.3831
, so that the final values
are respectively 0.3831 ![]() as and
as and ![]() as.
as.
The same remark which leads to the calculation of out-of-phase terms depending
on ![]() can be done for the other coefficients, but these out-of-phase terms
are respectively much smaller, so that even the semi-annual term gives a component
smaller than 1
can be done for the other coefficients, but these out-of-phase terms
are respectively much smaller, so that even the semi-annual term gives a component
smaller than 1![]() , that is to say
, that is to say ![]() for
for ![]() and
and ![]() for
for ![]() , where
, where ![]() is the mean
longitude of the Sun.
is the mean
longitude of the Sun.
 |
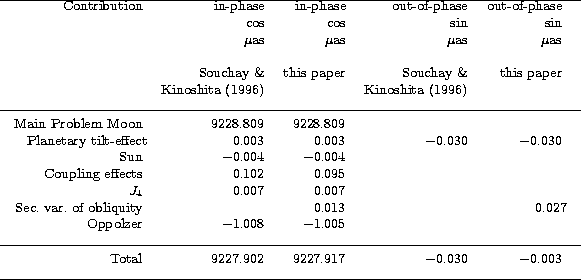 |
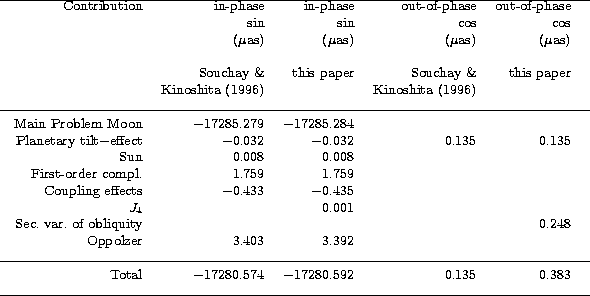
In Tables 3.1 and 3.2 we present our final values for the rigid Earth nutation leading
18.6y component, respectively in longitude and in obliquity, with the detailed account
of all the effects. The difference with Souchay & Kinoshita (1997) is, in milliarcsecond:
![]() and:
and:
![]() .The big differences for the out-of-phase components come from the new contribution related
to the secular variation of the obliquity, as detailed above.
.The big differences for the out-of-phase components come from the new contribution related
to the secular variation of the obliquity, as detailed above.
Copyright The European Southern Observatory (ESO)