

Up: The distribution of nearby Hipparcos
Subsections
We succeed in estimating individual ages from Strömgren photometry
(Figueras et al. 1991;
Masana 1994;
Asiain et al. 1997)
for a third of the sample (see Paper II).
To rule out any bias coming from an analysis of this sub-sample alone, we propose an
empirical palliative age estimation method based on the
Hipparcos absolute
magnitude and colour for the rest of the sample. On a first step, we use existing ages
to draw a plot of ages versus (Mv, (B-V)). A primary age parameter is assigned as
the mean age associated to a given range of (Mv, (B-V))
(Sect. 3.1). Then Strömgren age data are used a second time to assign
a probability distribution of palliative ages as a function of the primary age
parameter (Sect. 3.2).
Strömgren ages are available for 1077 A-F type stars with spectral types later than
A3 (B-V 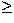 0.08) because the metallicity cannot be determined for A0-A3 spectral
types. With this sub-sample a relation between the absolute magnitude Mv, the
colour indice B-V and the age has been calibrated on a grid to extrapolate a less
accurate age for the rest of our sample (1900 stars). Since the relation cannot be
calibrated with Strömgren ages for spectral types between A0 and A3, we add 30 known
very young stars (
0.08) because the metallicity cannot be determined for A0-A3 spectral
types. With this sub-sample a relation between the absolute magnitude Mv, the
colour indice B-V and the age has been calibrated on a grid to extrapolate a less
accurate age for the rest of our sample (1900 stars). Since the relation cannot be
calibrated with Strömgren ages for spectral types between A0 and A3, we add 30 known
very young stars (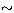 107 yr) belonging to the Centaurus-Crux association (see
Sect. 4) which have B-V
107 yr) belonging to the Centaurus-Crux association (see
Sect. 4) which have B-V 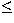 0.08. Consequences on the inferred
age distribution are investigated in Sect. 3.2. Available Strömgren
ages are averaged on a
0.08. Consequences on the inferred
age distribution are investigated in Sect. 3.2. Available Strömgren
ages are averaged on a 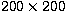 grid, ranging from [-0.5, 2.5] in absolute
magnitude and [-0.1, 0.6] in B-V. The result is smoothed and extrapolated to empty
cells, where feasible, using a
grid, ranging from [-0.5, 2.5] in absolute
magnitude and [-0.1, 0.6] in B-V. The result is smoothed and extrapolated to empty
cells, where feasible, using a 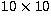 moving window. This process produces a
primary age parameter (Fig. 2). In Fig. 3,
Strömgren age indicators are plotted against this primary age parameter. Obviously,
there is not a one to one relation between the primary age parameter and the
Strömgren age. Very young Strömgren ages are the most affected by the degeneracy of
this relation; while the bulk of primary age parameters older than
moving window. This process produces a
primary age parameter (Fig. 2). In Fig. 3,
Strömgren age indicators are plotted against this primary age parameter. Obviously,
there is not a one to one relation between the primary age parameter and the
Strömgren age. Very young Strömgren ages are the most affected by the degeneracy of
this relation; while the bulk of primary age parameters older than
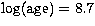 are in relatively good agreement with Strömgren ages. Only 14 among the 1900
stars have (Mv,(B-V)) out of the calibrated grid and do not have primary age
parameter. On the basis of Fig. 3, we can assign a probability
distribution for the Strömgren age to each primary age parameter.
are in relatively good agreement with Strömgren ages. Only 14 among the 1900
stars have (Mv,(B-V)) out of the calibrated grid and do not have primary age
parameter. On the basis of Fig. 3, we can assign a probability
distribution for the Strömgren age to each primary age parameter.
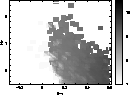 |
Figure 2:
Primary age parameter versus (Mv,(B-V)) relationship calibrated with the
Strömgren sub-sample. Grey levels represent the log(age)
value |
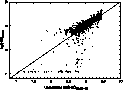 |
Figure 3:
Primary age parameter versus Strömgren age |
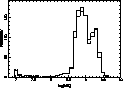 |
Figure 4:
Strömgren age distribution obtained with 1077 stars (full line) and
palliative age distribution for the same sub-sample (dotted line) |
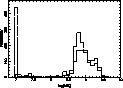 |
Figure 5:
Strömgren age distribution obtained with 1077 stars (full line) and
palliative age distribution for the remainder, i.e. stars without Strömgren
photometry (dotted line) |
Given a primary age parameter i, Fig. 3 can be read as giving
a discrete probability distribution P(j/i) of Strömgren ages j under i.
P(j/i) is given by:
| 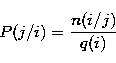 |
(8) |
where n(i,j) is the number of stars in cell (i,j) and
| 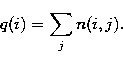 |
(9) |
These probabilities are discrete on a grid with an adaptive bin size to keep at least 3
stars per bin. This process produces a palliative age distribution which is free from
possible biases affecting the sub-sample of stars with Strömgren photometry for
stars with B-V 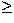 0.08.
0.08.
The small deviations from the distribution of original Strömgren ages
(Fig. 4) are due to finite bin steps used in the discretisation
process. The palliative age distribution of the sub-sample without Strömgren
photometry (Fig. 5) shows a great difference for very young ages
with respect to the Strömgren age distribution. The great peak at
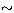 107 yr partly results from the poor calibration of the relation between age
and (Mv, (B-V)) for B-V
107 yr partly results from the poor calibration of the relation between age
and (Mv, (B-V)) for B-V 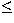 0.08. If the calibration of the relation is
realized without the additional Centaurus-Crux stars, we would obtain a frequency, at
0.08. If the calibration of the relation is
realized without the additional Centaurus-Crux stars, we would obtain a frequency, at
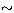 107 yr, of
107 yr, of 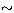 170 stars instead of
170 stars instead of 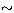 440 stars. It means that
there are at least 170 stars of few 107 year old and that the difference of
440 stars. It means that
there are at least 170 stars of few 107 year old and that the difference of 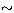 270 stars is composed of A0-A3 type stars which may be older. How older are they?
Using theoretical isochrones from
Bertelli et al. (1994), a relation
between the total lifetime of a star at the turnoff point and the color indice (B-V)
can be infered. We can show that the total lifetimes of A0-A3 type stars are between
4-6 108 yr, if the metallicity of the stars are between Z=0.008 and Z=0.02.
Taking the half lifetime of the star as the most probable age, we obtained, for these
270 stars, an age distribution in the range 2-3 108 yr (
270 stars is composed of A0-A3 type stars which may be older. How older are they?
Using theoretical isochrones from
Bertelli et al. (1994), a relation
between the total lifetime of a star at the turnoff point and the color indice (B-V)
can be infered. We can show that the total lifetimes of A0-A3 type stars are between
4-6 108 yr, if the metallicity of the stars are between Z=0.008 and Z=0.02.
Taking the half lifetime of the star as the most probable age, we obtained, for these
270 stars, an age distribution in the range 2-3 108 yr (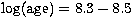 ).
This distribution of these half lifetimes remains very well separated from the older
stars in the sample.
To summarize, the great peak at 107 yr contains at least 170 stars of
).
This distribution of these half lifetimes remains very well separated from the older
stars in the sample.
To summarize, the great peak at 107 yr contains at least 170 stars of
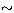 107 yr and 270 stars for which ages may spread up to 3 108 yr. These
stars belong to the younger part of the sample.
107 yr and 270 stars for which ages may spread up to 3 108 yr. These
stars belong to the younger part of the sample.
The palliative ages are statistical
ages. Hence, they sometimes produce artifacts or young ghost peaks in some stream age
distributions. Such dummy young peaks will always appear as the weak counterpart of a
heavy peak around 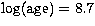 . Nevertheless palliative ages permit to shed
light on the age content of the phase space structures when Strömgren data are
sparse.
. Nevertheless palliative ages permit to shed
light on the age content of the phase space structures when Strömgren data are
sparse.


Up: The distribution of nearby Hipparcos
Copyright The European Southern Observatory (ESO)




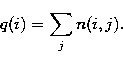
![]() 107 yr partly results from the poor calibration of the relation between age
and (Mv, (B-V)) for B-V
107 yr partly results from the poor calibration of the relation between age
and (Mv, (B-V)) for B-V ![]() 0.08. If the calibration of the relation is
realized without the additional Centaurus-Crux stars, we would obtain a frequency, at
0.08. If the calibration of the relation is
realized without the additional Centaurus-Crux stars, we would obtain a frequency, at
![]() 107 yr, of
107 yr, of ![]() 170 stars instead of
170 stars instead of ![]() 440 stars. It means that
there are at least 170 stars of few 107 year old and that the difference of
440 stars. It means that
there are at least 170 stars of few 107 year old and that the difference of ![]() 270 stars is composed of A0-A3 type stars which may be older. How older are they?
Using theoretical isochrones from
Bertelli et al. (1994), a relation
between the total lifetime of a star at the turnoff point and the color indice (B-V)
can be infered. We can show that the total lifetimes of A0-A3 type stars are between
4-6 108 yr, if the metallicity of the stars are between Z=0.008 and Z=0.02.
Taking the half lifetime of the star as the most probable age, we obtained, for these
270 stars, an age distribution in the range 2-3 108 yr (
270 stars is composed of A0-A3 type stars which may be older. How older are they?
Using theoretical isochrones from
Bertelli et al. (1994), a relation
between the total lifetime of a star at the turnoff point and the color indice (B-V)
can be infered. We can show that the total lifetimes of A0-A3 type stars are between
4-6 108 yr, if the metallicity of the stars are between Z=0.008 and Z=0.02.
Taking the half lifetime of the star as the most probable age, we obtained, for these
270 stars, an age distribution in the range 2-3 108 yr (![]() ).
This distribution of these half lifetimes remains very well separated from the older
stars in the sample.
To summarize, the great peak at 107 yr contains at least 170 stars of
).
This distribution of these half lifetimes remains very well separated from the older
stars in the sample.
To summarize, the great peak at 107 yr contains at least 170 stars of
![]() 107 yr and 270 stars for which ages may spread up to 3 108 yr. These
stars belong to the younger part of the sample.
107 yr and 270 stars for which ages may spread up to 3 108 yr. These
stars belong to the younger part of the sample.
![]() . Nevertheless palliative ages permit to shed
light on the age content of the phase space structures when Strömgren data are
sparse.
. Nevertheless palliative ages permit to shed
light on the age content of the phase space structures when Strömgren data are
sparse.