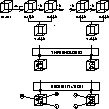
 |
Figure 1: Implementation of the wavelet analysis |
 |
(1) |
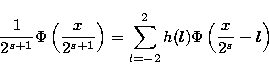 |
(2) |
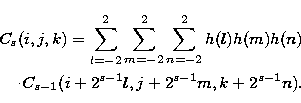 |
||
| (3) |
| Ws(i,j,k)=Cs-1(i,j,k)-Cs(i,j,k). | (4) |
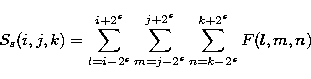 |
(5) |
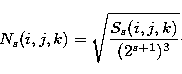 |
(6) |
The local threshold ![]() is inferred from the local noise
Ns(i,j,k) through calibration curves established by numerical simulations
(see
Sect. 2.3) which link it to the noise Ns(i,j,k).
Then the hard-thresholding on wavelet coefficients follows:
is inferred from the local noise
Ns(i,j,k) through calibration curves established by numerical simulations
(see
Sect. 2.3) which link it to the noise Ns(i,j,k).
Then the hard-thresholding on wavelet coefficients follows:
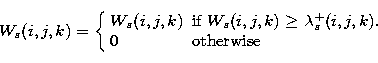
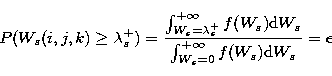 |
(7) |
Copyright The European Southern Observatory (ESO)