2 Compiled catalogue

 

2.1 Stellar content

The basic set of 2033 stars down to $V=16.8^{\rm m}$ was extracted from the Tautenburg survey which provides the most complete list of stars in the NGC 6611 region. The observations, measurements, procedures for proper motion and B, V determination as well as the accuracy of the Tautenburg data are described in KS95. The list was completed by adding 152 bright stars and close optical companions found in the literature. On Schmidt plates, these stars could not be measured properly due to a crowding effect.

Figure 1 shows a map of all 2185 stars included in the compiled catalogue in the NGC 6611 region. The V magnitudes of the stars range from $8.01^{\rm m}$ to $16.78^{\rm m}$. The coordinates of the cluster center as determined in this study are ($\alpha,\delta)_{2000.0}=18^{\rm h}18^{\rm m}40^{\rm s},-13^\circ 47.1'$ (see Table 3).

  

Figure 1: Distribution of field stars (triangles) and the cluster members (open circles) of the survey within the NGC 6611 region. The size of symbols corresponds to the brightness of stars. The magnitude range is $\Delta V=8.01-16.78^{\rm m}$. The coordinates X,Y are given in arcmin with respect to the Walker's star 125 ($\alpha,\delta)_{2000.0}=18^{\rm h}18^{\rm m}26.21^{\rm s}$, $-13^\circ 50' 05.3''$ and increase with right ascension (X) and declination (Y)

2.2 Coordinates

Right ascensions and declination ($\alpha, \delta$) were computed from the plate coordinates measured on the Tautenburg first epoch (1963.45) plate with respect to 51 PPM stars (V from $6.52^{\rm m}$ to $10.13^{\rm m}$) uniformly distributed over the field. The solutions were carried out with the least squares technique applied to polynomials

$$\begin{tabular} {lcl} $\xi - X $\space & =& $ Q_a(X,Y) + a_1... ...- Y $& =& $ Q_b(X,Y) + b_1 Y (X^2 + Y^2) + b_2 B.$\end{tabular}$$ (1)

Here B stands for a stellar magnitude, $\xi$, $\eta$ are tangential coordinates with respect to the plate center and Q(X,Y) is a complete 2-nd order polynomial. We determined a magnitude equation in the Y coordinate as $b_2=(22~\pm~5)~10^{-4}$ mm/mag and the distortion terms due to the curvature of the Schmidt plate as $a_1=(2.05~\pm~0.20)~10^{-8}$ mm^-2 and $b_1=(1.41~\pm~0.18)~10^{-8}$ mm^-2. Coefficient a₂ is found to be insignificant. The accuracy of the right ascension and declination at the epoch 1963.45 is 0.008 s and 0.14 arcsec, respectively. For the final version of the catalogue, the coordinates were recomputed for the equinox 2000.0 and epoch 1990.77.

For 99 stars not measured on the Tautenburg plates, the positions were taken from Hillenbrand et al. (1993) where the equatorial coordinates were derived for the equinox 2000.0 with the Guide Star Catalog (GSC) as a reference. 53 stars of Walker (1961) could not be found either in the Tautenburg survey (KS95) or in the list of Hillenbrand et al. (1993). For these stars, only their approximate rectangular coordinates taken from Walker's (1961) maps are given in the catalogue.

2.3 Absolute proper motions

2.3.1 Tautenburg proper motion survey (KS95)

Relative proper motions were derived from the measurements of the Tautenburg plates with respect to a large sample of anonymous stars (some 13000 stars) selected among field stars with small proper motions. The proper motions of stars with the highest probability to belong to one of the four open clusters (Trümpler 32, NGC 6611, C 1819-146, C 1820-146) identified on the plates were used to correct the proper motions of all other stars for a magnitude-dependent error (see KS95).

The accuracy of the Tautenburg proper motions was estimated as 2.7 mas/year from a comparison of our data with the results published by Van Schewick (1962), Kamp (1974) and Tucholke et al. (1986) for the stars in common ($B=9.8^{\rm m}-14.6^{\rm m}$). Outside of this magnitude range the proper motion accuracy is lower and decreases rapidly for stars fainter than B = $16^{\rm m}$.A dependence of the proper motion rms error $\varepsilon_{\mu}$ on magnitudes within $B=7^{\rm m}-17^{\rm m}$ was found to be best fitted by a polynomial

$$\begin{tabular} {lcl} $\varepsilon_{\mu} [{\rm mas/y}]$& =& ... ...3)^3 $\\ & & $- 0.4478 (B-13) + 2.6832.$\space \\ \end{tabular}$$ (2)

Since no galaxies could be found in this direction of the sky, we originally used PPM-South stars (Bastian & Röser 1993) in KS95 to convert the relative proper motions from the Tautenburg survey to absolute ones. Meanwhile, the Hipparcos catalogue (ESA 1997) is available, so we re-computed the zero point corrections for the Tautenburg proper motions with respect to the Hipparcos reference system. Although 22 Hipparcos stars were identified in the Tautenburg survey covering a field of 8.95 sq. degrees, one half of them was too bright to be properly measured on Schmidt plates. The zero point corrections for the Tautenburg proper motions with respect to the Hipparcos reference system were computed to be

After the Tautenburg data were corrected for the zero point and magnitude-dependent errors, we assume KS95 to represent the proper motion system on which the compiled catalogue is now based.

2.3.2 Proper motions (H/KS) for Hillenbrand et al. (1993) stars

Whereas proper motions for the bright stars in the NGC 6611 region were determined by several authors, there are only two studies, KS95 and Hillenbrand et al. (1993), where astrometric information for stars fainter than $V=15^{\rm m}$ is presented. That was the main reason to include CCD-positions obtained by Hillenbrand et al. (1993) in our catalogue. In their paper the authors listed the equatorial coordinates of about 1000 stars for the equinox 2000.0 and epoch 1990.77. The coordinates were derived in the system of the GSC. The accuracy of positions was estimated by the authors to be 0.2 arcsec. Proper motions were derived by combining these positions with the coordinates at the epoch 1963.45 computed according to Eq. (1) from measurements of the first epoch plate of the Tautenburg survey. The sample is marked by H/KS in Table 1. Taking into account the accuracy of the Tautenburg and CCD-positions and a time-span of 27.32 years, a formal error of 9 mas/yr may be expected for these proper motions. Nevertheless, from a comparison of the proper motions from H/KS with the data of Van Schewick (1962), Kamp (1974) and Tucholke et al. (1986) an accuracy of 4.6 mas/yr was estimated for the stars in common ($B=8.0^{\rm m}-14.6^{\rm m}$). This result indicates that at least for these stars the errors seem to be overestimated both for the Tautenburg and CCD-positions from Hillenbrand et al. (1993). For the Tautenburg survey this conclusion seems to be justified because the error of 0.12-0.14 arcsec given in Chapter 2.2 for the coordinates refers to stars distributed over the whole field covered by a Tautenburg plate (c.a. 9 sq.degrees) whereas the cluster NGC 6611 is located close to the plate center. As in Hillenbrand et al. (1993) the coordinates were used exclusively for the identification reasons, the authors gave only a brief description of the atrometric reduction applied. In any case, we may conclude that the accuracy of the Hillenbrand et al. (1993) coordinates should be better than the authors assumed.

  

Table 1: Proper motion catalogues used for the construction of the compiled catalogue

0.8ex

Using the data from KS95 and H/KS, one has to take into account that the proper motions are highly correlated since they are based on the same first epoch observations. They differ due to the second epoch observations and the reduction method applied. The Tautenburg proper motions were derived by a plate-to-plate reduction with a time baseline of 24.2 years. The H/KS proper motions were computed from differences of equatorial coordinates for the equinox 2000.0 over a time-span of 27.32 years.

2.3.3 Compilation of the proper motions

In order to derive proper motions in a common system, we applied a method which is generally used for the construction of compilation catalogues (e.g., Eichhorn 1974). Each proper motion catalogue from Table 1 was reduced to the system of the Tautenburg survey (KS95) by correction for different zero points and magnitude-dependent errors.

In order to determine weights for each catalogue, we used about 250 stars with at least three independent proper motion determinations (note: the catalogue pairs KS95 and H/KS as well as Van Schewick (1962) and Tucholke et al. (1986) were considered as correlated catalogues). From proper motion residuals of the same stars included in three catalogues, external rms errors of each catalogue could be estimated (see KS95). The corresponding rms errors which were used to define weights of the catalogues are given in the last column of Table 1. These weights were used in computing the mean proper motions and the corresponding rms errors for stars of the compiled catalogue. For the stars whose proper motions were obtained with the Tautenburg plates only, the rms errors were computed according to Eq. (2). Figure 2 shows the differences of proper motions from the compiled catalogue and the source catalogues. Only those stars are plotted which appear in at least two catalogues listed in Table 1.

  

Figure 2: Differences in proper motions between the compiled and the original catalogues (see Table 1) as a function of V

In total, our catalogue contains proper motions for 2074 stars. To check these proper motions for possible magnitude-dependent errors, we used data on cluster members with the assumption that the proper motions of cluster stars are independent of the apparent magnitude. Figure 3 shows absolute proper motions versus stellar magnitude V for all 2074 stars and for probable cluster members.

  

Figure 3: Absolute proper motion components in X and Y directions versus V magnitude. Dots: all stars included in the compiled catalogue; open circles: stars with the highest membership probability based both on proper motions and coordinates; crosses: stars with the highest membership probability based on proper motions only

According to Fig. 3, we can conclude that the proper motions are free from magnitude-dependent errors both in X and Y directions.

2.4 Photometric data

The calibration of B and V Tautenburg plates in KS95 was based on photoelectric sequences taken from Walker (1961), Sagar & Joshi (1979), and Nicolet (1978). The background effect due to M 16 was taken into account in photographic magnitudes by a term

where $\overline X, \overline Y$ are the coordinates of the centre of M 16. For the factor k values of $0.25^{\rm m}\pm 0.06$, $0.32^{\rm m}\pm 0.04$ and $0.15^{\rm m}\pm 0.04$ were obtained for two B plates and one V plate, respectively. The accuracy of the photometric data was estimated as $\sigma_B=\pm 0.12^{\rm m}$ and $\sigma_V=\pm 0.10^{\rm m}$ (see KS95).

In addition, we included the relevant data from the photometric catalogues obtained in the NGC 6611 region (see Table 2).

  

Table 2: Photometric catalogues used for the construction of the compiled catalogue

0.2ex

The photometric UBV system of the compiled catalogue is defined by the common photoelectric sequences described below. Since the accuracy of the photoelectric data achieved by the authors from Table 2 is comparable, we assumed equal weights for all photoelectric catalogues. However, from a comparison of magnitudes for stars in common, we found systematic differences between the data of Walker (1961), Sagar & Joshi (1979), Thé et al. (1990) on one side and Hoag et al. (1961), Hiltner & Morgan (1969) on the other side. Especially, for U magnitudes this effect was highly significant (see Fig. 4).

  

Figure 4: Differences in magnitudes, colors and color excesses between the compiled catalogue and the original photoelectric data (see Table 2) versus V magnitudes. Small, medium and large circles indicate stars with $(B-V)\leq 0.5^{\rm m}$, 0.5 $<(B-V)\leq0.8^{\rm m}$ and $(B-V)\gt.8^{\rm m}$,respectively

  

Figure 5: Differences in magnitudes and colors between the compiled catalogue and original CCD and photographic data (see Table 2). Small, medium and large open circles indicate the stars with $(B-V)\leq 0.5^{\rm m}$, 0.5$<(B-V)\leq0.8^{\rm m}$ and $(B-V)\gt.8^{\rm m}$,respectively. Only stars with photoelectrically determined magnitudes and colors are plotted

Therefore, the photometric reduction was performed in three steps: for each of the two groups, we derived its own photoelectric system; the common photoelectric system was defined as the mean of the intermediate systems; finally, the corresponding zero point correction was introduced in the original magnitude for each star. A similar procedure was applied to the original color excesses E_(B-V) to combine them into a common system. Our catalogue includes 121, 118, 115 and 97 stars with photoelectric V magnitudes, (B-V), (U-B) and color excesses E_(B-V), respectively.

For stars without photoelectric data, magnitudes and colors in our catalogue are based on CCD and photographic measurements. A deep CCD photometry was obtained in the NGC 6611 region by Hillenbrand et al. (1993). An analysis of these data (Fig. 5) showed that they differed systematically by a few $0.01^{\rm m}$ from the compiled photoelectric system which we assumed to be the most reliable.

From a comparison of the photoelectric and CCD sequences, we computed the corrections to $UBV_{\rm CCD}$ magnitudes of Hillenbrand et al. (1993) as

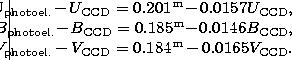The photographic data from KS95 and Walker (1961) were also reduced to the compiled photoelectric system. The U, B, V magnitudes of stars without photoelectric photometry were computed as weighted mean values of the reduced CCD and photographic data. Weights for the CCD data were determined from rms errors given in Hillenbrand et al. (1993) as a function of the V magnitudes (their Fig. 3). For photographic data, much higher rms errors, $\sigma_V=\pm 0.10^{\rm m}$, $\sigma_B=\pm 0.12^{\rm m}$, and $\sigma_U=\pm0.15^{\rm m}$, were assumed.

Thus all UBV photometric data were derived into a common system based on the photoelectric sequence described above. Totally, our catalogue includes 2185 stars with V magnitudes and (B-V) color indexes, 917 stars with (U-B) color indexes and 97 stars with E_(B-V) color excesses. For completeness, the original infrared JHK photometry obtained by Hillenbrand et al. (1993) from CCD observations are also given in the compiled catalogue (384 stars).

2.5 Cluster membership probabilities

For such distant clusters as NGC 6611, the extraction of members from proper motions only is rather uncertain due the low significance of the differences between individual proper motions of cluster members and distant field stars. On the other hand, distant clusters show a local concentration of stars in the projection on the sky which provides an additional criterion for the selection of members.

In order to improve the reliability of membership determination, we applied a statistical method described in KS95 and Kharchenko et al. (1997) which used the information both position and proper motion distributions of stars in the cluster neighbourhood.

The distribution function $F(\mu_X,\mu_Y,X,Y)$ of stars in the vicinity of a cluster is assumed to be the sum of two distribution functions of field and cluster stars, respectively:

The cluster distribution itself can be divided in two components, the core and corona distributions which have different spatial dispersions. The field stellar population is not homogeneous also, since field stars being observed at different distances have different kinematical properties. Therefore, the distribution function of proper motions of field stars can be regarded again as the sum of at least two components (near and distant). So we get

We assume normal distributions for proper motions of field and cluster stars. Also, the spatial distribution of cluster members is normal distribution, whereas field stars are uniformly distributed over the area. The parameters of the distribution functions were derived in a four-dimension space of proper motions ($\mu_X, \mu_Y$) and plate coordinates (X, Y) by applying the maximum likelihood technique. To increase the stability of the solution, we only considered 656 stars with $V < 16.0^{\rm m}$ and proper motion less than 50 mas/y. The results of the solution are given in Table 3.

  

Table 3: Parameters of the distribution functions in the NGC 6611 region

3ex

  

Figure 6: Reddening map of the NGC 6611 region. The size of the filled circles is proportional to the color excess value averaged over $2'\times2'$ cells. Stars from our catalogue brighter than $11.0^{\rm m}$ are plotted, too (open circles, with sizes proportional to stellar magnitudes). Radial distances $r = 3\sigma_{X\,Y}^{\rm core}$ (solid line) and $r = 3 \sigma_{X\,Y}^{\rm corona}$ (dashed line) are also indicated

  

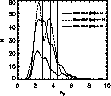Figure 7: Distribution of 467 catalogue stars with different cluster membership probabilities over AV. Dotted-dashed line: stars with proper motion membership probability $P({\rm pm}) \gt 63\%$; solid line: stars with $P({\rm pm})\gt 14\%$; dashed line: stars with $P({\rm pm}) \le 14\%$.Four absorption groups showed in Fig. 8 are separated provisionally by dotted-dashed vertical lines

The cluster membership probabilities for the core and corona were computed as

where t_i denote proper motions $\mu_X$, $\mu_Y$ or coordinates X, Y (K = 4); $\overline {t_i}$ and $\sigma_{t_i}$ are the corresponding mean values and dispersions. The membership probabilities based on proper motions alone (K = 2) are also given in our catalogue. The stars with membership probabilities higher than 61%, 14%, 1% are located at distances less than $1\sigma$, $2\sigma$, $3\sigma$ from the maximum of the distribution function and were considered as high probable, probable or low probable members, respectively.

Absolute proper motions of NGC 6611 along the Y axis (direction of the Galactic rotation) and Z axis (direction to the Galactic North Pole) are $+2.49 \pm 0.11$ and $-0.25 \pm 0.10$ mas/year, respectively. This corresponds to spatial velocity components of $V_Y = +24.8 \pm 1.1$and $V_Z=-2.5\pm1.0$ km s^-1.