

Up: The use of minimal distribution
Subsections
The goal of this part is to calibrate the method with a high quality sample
in order to allow a future more extensive application.
We use a subsample of the regular and richest clusters of galaxies described
in Adami et al. (1998) to study the variation of the
galaxy aggregation with magnitude. We have used in this article COSMOS
(bj magnitude) and APM surveys (b magnitude). We keep here only the
richest clusters with more than 180 galaxies
brighter than bj=20 or b=20 (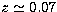 and
and 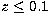 ) in a 5
) in a 5 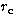 area (at 5
area (at 5 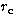 from the center, the surface density is only 1% of the
central density if we assume a King profile; Therefore we have the main part
of the cluster) and without apparent substructures (15 clusters). We exclude
finally the clusters with an atypical King core radius (greater than 300 kpc).
from the center, the surface density is only 1% of the
central density if we assume a King profile; Therefore we have the main part
of the cluster) and without apparent substructures (15 clusters). We exclude
finally the clusters with an atypical King core radius (greater than 300 kpc).
We have sorted the galaxies by magnitude (bj magnitudes). For each cluster,
we select some sets of 125 consecutive galaxies out of the 180 (or more)
between the 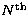 and the (
and the (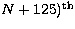 ranked galaxies. For each of
those, we calculate the distance
ranked galaxies. For each of
those, we calculate the distance 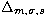 and the error for
this distance with the corresponding uniform sample. With N=0, 10, 20, 30, 40,
50, 60 etc., we are able to have many determinations of
and the error for
this distance with the corresponding uniform sample. With N=0, 10, 20, 30, 40,
50, 60 etc., we are able to have many determinations of
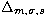 . We note however that these ranges are not
independent. This allows us to compute a variation of the aggregation level with
the magnitude. We search for a negative slope, characterizing an increasing
aggregation for the bright magnitudes. The selected clusters and the
characteristic results are listed in Table 1.
. We note however that these ranges are not
independent. This allows us to compute a variation of the aggregation level with
the magnitude. We search for a negative slope, characterizing an increasing
aggregation for the bright magnitudes. The selected clusters and the
characteristic results are listed in Table 1.
Table 1:
Characteristic parameters of the selected clusters: name,
number of galaxies, slope of the 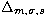 /magnitude
relation, redshift and type of the data (COSMOS/APM)
/magnitude
relation, redshift and type of the data (COSMOS/APM)
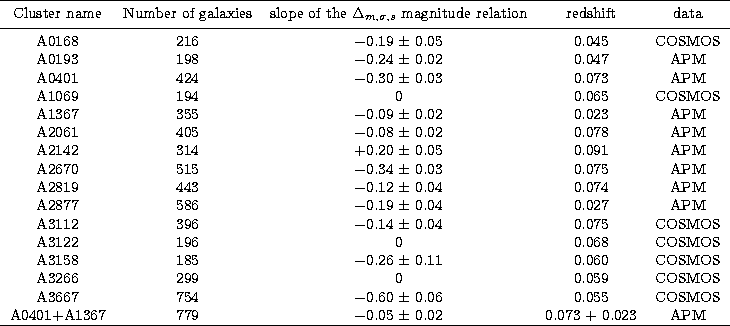 |
The clusters A1069, A3122 and A3266 have not a significant tendency at
the 1  level: the regression line between
level: the regression line between 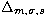 and the magnitude have a slope equal to 0. The cluster A2142 shows a positive
slope (i.e. a decreasing aggregation for the bright magnitudes). The other
clusters (75% of the sample) exhibit a significant decreasing tendency at
the 1
and the magnitude have a slope equal to 0. The cluster A2142 shows a positive
slope (i.e. a decreasing aggregation for the bright magnitudes). The other
clusters (75% of the sample) exhibit a significant decreasing tendency at
the 1  level.
Our simulations do not take into account a possible background contribution.
Such a contamination could reduce the efficiency of the discrimination. We
test here two kinds of contamination: a uniform one (uniform density of
background galaxies) and a clustered one (presence of secondary groups on
the same line of sight).
In order to test this point, we have selected the cluster A3158 in an area
of 2 Mpc. According to the background level computed in Adami et al. (1998),
the ratio (C hereafter) between the background galaxies and the cluster
members is 3.7. In this area, the
level.
Our simulations do not take into account a possible background contribution.
Such a contamination could reduce the efficiency of the discrimination. We
test here two kinds of contamination: a uniform one (uniform density of
background galaxies) and a clustered one (presence of secondary groups on
the same line of sight).
In order to test this point, we have selected the cluster A3158 in an area
of 2 Mpc. According to the background level computed in Adami et al. (1998),
the ratio (C hereafter) between the background galaxies and the cluster
members is 3.7. In this area, the 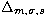 distance is
significantly different from 0. We are able to see the structure (Fig. 7).
distance is
significantly different from 0. We are able to see the structure (Fig. 7).
We increase artificially C by uniformly adding galaxies in
the selected field of view. For each set of added galaxies, we make 100
realizations in order to compute an error for 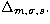 We show
in Fig. 7 the variation of
We show
in Fig. 7 the variation of 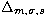 with C. We can see that
with C. We can see that
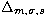 is significantly different from 0 (according to the
error bars) for
is significantly different from 0 (according to the
error bars) for 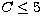 . For
. For 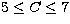 ,
, 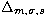 is
different of 0 in more than 50% of the realizations. For
is
different of 0 in more than 50% of the realizations. For 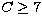 , we are
not able to distinguish the cluster structure in more than 50% of the 100
realizations.
, we are
not able to distinguish the cluster structure in more than 50% of the 100
realizations.
We conclude that we are able to make the difference between the cluster and
the field even if the ratio C is equal to 5, and probably 7. The influence
of a uniform background level is therefore minor.
![\begin{figure}
\includegraphics[angle=-90,width=8.8cm,clip]{fig8.ps}\end{figure}](/articles/aas/full/1999/02/ds7993/Timg39.gif) |
Figure 7:
Variation of 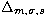 for A3158 with different ratio
C between the number of background and cluster galaxies for A3158 with different ratio
C between the number of background and cluster galaxies |
The other possible contamination is that of secondary groups or clusters on
the same line of sight. To test this effect, we have built a composite
cluster: we have superposed the cluster A0401 (z=0.073) and the cluster
A1367 (z=0.023). The contribution of A1367 will then add a signal of structure
on the line of sight. We see that we destroy almost all the decrease of
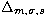 : the slope of the regression is
: the slope of the regression is 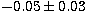 (see
Table 1). This kind of contamination can erase the variation of the distance
(see
Table 1). This kind of contamination can erase the variation of the distance
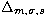 with magnitude.
with magnitude.


Up: The use of minimal distribution
Copyright The European Southern Observatory (ESO)
![]() and the (
and the (![]() ranked galaxies. For each of
those, we calculate the distance
ranked galaxies. For each of
those, we calculate the distance ![]() and the error for
this distance with the corresponding uniform sample. With N=0, 10, 20, 30, 40,
50, 60 etc., we are able to have many determinations of
and the error for
this distance with the corresponding uniform sample. With N=0, 10, 20, 30, 40,
50, 60 etc., we are able to have many determinations of
![]() . We note however that these ranges are not
independent. This allows us to compute a variation of the aggregation level with
the magnitude. We search for a negative slope, characterizing an increasing
aggregation for the bright magnitudes. The selected clusters and the
characteristic results are listed in Table 1.
. We note however that these ranges are not
independent. This allows us to compute a variation of the aggregation level with
the magnitude. We search for a negative slope, characterizing an increasing
aggregation for the bright magnitudes. The selected clusters and the
characteristic results are listed in Table 1.
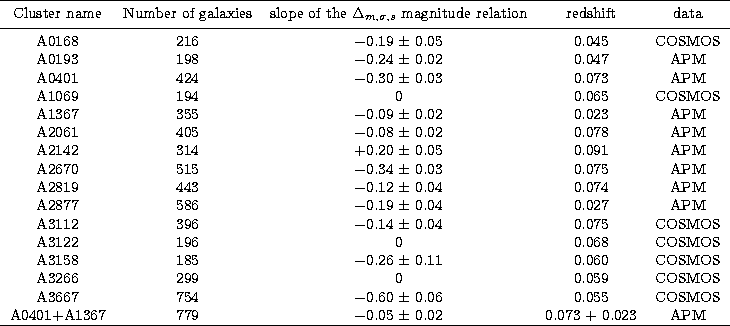
![]() We show
in Fig. 7 the variation of
We show
in Fig. 7 the variation of ![]() with C. We can see that
with C. We can see that
![]() is significantly different from 0 (according to the
error bars) for
is significantly different from 0 (according to the
error bars) for ![]() . For
. For ![]() ,
, ![]() is
different of 0 in more than 50% of the realizations. For
is
different of 0 in more than 50% of the realizations. For ![]() , we are
not able to distinguish the cluster structure in more than 50% of the 100
realizations.
, we are
not able to distinguish the cluster structure in more than 50% of the 100
realizations.
![\begin{figure}
\includegraphics[angle=-90,width=8.8cm,clip]{fig8.ps}\end{figure}](/articles/aas/full/1999/02/ds7993/Timg39.gif)