

Up: The use of minimal distribution
Subsections
The MST is a geometrical construction issued from the graph theory: the used
definitions are given in Dussert (1988). Very briefly, it is a tree
joining all the points of a given set, without a loop and with a minimal
length; each point is visited by the tree only 1 time. The main aspect here
is the unicity of such a construction. For a given set of points, there are
more than 1 MST, but the histogram H of the MST edges is unique. This is
fundamental because it is then possible to completely characterize a set of
points with H.
Traditionally, only the two first momenta of H mean m and dispersion
 are used. These two parameters are efficient for a Gaussian
distribution. To
characterize some non Gaussian distributions, we have to use more advanced
momenta like the skewness s and/or the curtosis c. We have tested the use of
these parameters in the following. Below, we describe the methodology:
are used. These two parameters are efficient for a Gaussian
distribution. To
characterize some non Gaussian distributions, we have to use more advanced
momenta like the skewness s and/or the curtosis c. We have tested the use of
these parameters in the following. Below, we describe the methodology:
- The Prim algorithm (1957) is used to construct the MST and
compute the histogram H of edges.
- A point is chosen at random in the set and is the first MST
element.
- A point which is the nearest of the MST point, is joined to the MST
and removed from the set. The first MST edge is between these two points.
- We look for the set point which is the nearest of the MST points,
join it to the MST and remove it from the set. The next MST edge is
between this point and its nearest MST point.
- We repeat the operation for all the other set points.
This algorithm is designed to be the fastest one to have a MST on a given
set of points. We normalize the lengths of the MST by using the
Beardwood
et al. (1959)
study. A good approximation of the total length of a MST constructed with a
random set of N points in an area S is 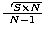 . So,
we divide all the length by this factor (where S is the area of the maximum
rectangle of the point set). We calculate finally the mean m, the dispersion
. So,
we divide all the length by this factor (where S is the area of the maximum
rectangle of the point set). We calculate finally the mean m, the dispersion
 , the skewness s and the curtosis c of H.
, the skewness s and the curtosis c of H.
We test our algorithm using simulations. We calculate m,  , s, c for
different sets of simulated points. The points are
generated in 500
, s, c for
different sets of simulated points. The points are
generated in 500 500 boxes. We note here that we normalize the
distances and so, the unity of the box size is not important.
500 boxes. We note here that we normalize the
distances and so, the unity of the box size is not important.
In order to characterize the cuspiness degree of the distributions,
we use three kind of 2D density profiles: points randomly distributed
(Poisson distribution), distributed with a centered King profile (flat
profile in the center) and distributed with a centered NFW profile (cusped
profile in the center: Navarro et al. 1995). We note here that the NFW
expression was for a 3D distribution. Applying it for a 2D set of points
generate a more cusped profile compared to the original 3D NFW. However, we
will speak of "NFW profiles'' hereafter. The way we generated sets of
points with a given profile is described in Adami (1998)
and is related to
the techniques described in Press et al. (1992). If 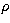 is the density
and r the radius, we have:
is the density
and r the radius, we have:
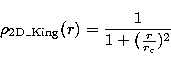
and
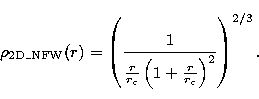
We will call hereafter 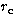 the characteristic radius of a given profile.
For the King profile, it is the core radius and for the NFW profile it is a
characteristic radius (no core for this profile). We simulate 8 sets of
random distributions: with 10, 25, 60, 125, 250, 500, 750 and 1000
points.
the characteristic radius of a given profile.
For the King profile, it is the core radius and for the NFW profile it is a
characteristic radius (no core for this profile). We simulate 8 sets of
random distributions: with 10, 25, 60, 125, 250, 500, 750 and 1000
points.
For each set of points with a given profile and a given size, we proceed 100
realizations and so 100 calculations of m,  , s, c. From these data, we
are able to compute the mean value and the dispersion of each parameter m,
, s, c. From these data, we
are able to compute the mean value and the dispersion of each parameter m,
 , s or c.
, s or c.
We plot in Fig. 1 (m,  ) and (s, c)
for a Poisson distribution.
) and (s, c)
for a Poisson distribution.
![\begin{figure}
\includegraphics[angle=-90,width=8.8cm,clip]{fig1.ps}\end{figure}](/articles/aas/full/1999/02/ds7993/Timg10.gif) |
Figure 1:
Variation with the size N of the sample of: up: (m,  ), m
is the upper line and ), m
is the upper line and  is the lower line and down: (s, c), s is the
line with error bars and c is the line without error bar is the lower line and down: (s, c), s is the
line with error bars and c is the line without error bar |
The parameters m and  are asymptotically equal to 0.66
are asymptotically equal to 0.66 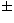 0.02
and 0.31
0.02
and 0.31 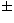 0.02 in perfect agreement with Dussert (1988). The error bars
are 3% of the mean value. The final value is reached for a number N of points
in the simulation greater than 125.
0.02 in perfect agreement with Dussert (1988). The error bars
are 3% of the mean value. The final value is reached for a number N of points
in the simulation greater than 125.
The skewness s is well defined for 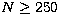 with a final value of
0.29
with a final value of
0.29 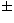 0.14. The errors are greater: about 50% of the mean value.
0.14. The errors are greater: about 50% of the mean value.
The curtosis c is well defined only for 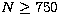 with very large error
bars (
with very large error
bars (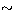 100% of the mean value). The final value is 0.33.
100% of the mean value). The final value is 0.33.
![\begin{figure}
\includegraphics[angle=-90,width=17cm,clip]{fig2.ps}\end{figure}](/articles/aas/full/1999/02/ds7993/Timg15.gif) |
Figure 2:
Variation with the characteristic radius of the King distribution
of: upper left: (m,  ) and 250 points (the increasing line is m and the
decreasing line is ) and 250 points (the increasing line is m and the
decreasing line is  ), upper right: (s, c) and 250 points (s is the
line with error bars and c is the line without error bar), lower left:
(m, ), upper right: (s, c) and 250 points (s is the
line with error bars and c is the line without error bar), lower left:
(m,  ) and 500 points (the increasing line is m and the decreasing line
is ) and 500 points (the increasing line is m and the decreasing line
is  ), lower right: (s, c) and 500 points (s is the line with error
bars and c is the line without error bar) ), lower right: (s, c) and 500 points (s is the line with error
bars and c is the line without error bar) |
We calculate (m,  , s, c)
for different characteristic radii
, s, c)
for different characteristic radii 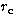 of
King and NFW profiles. We use
of
King and NFW profiles. We use 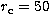 , 75, 100, 125, 150, 175, 200, 225,
250, 275 and 300 kpc. For a given profile and a given characteristic
radius, we simulate 2 sets of points: 250 and 500. We plot the variation
of (m,
, 75, 100, 125, 150, 175, 200, 225,
250, 275 and 300 kpc. For a given profile and a given characteristic
radius, we simulate 2 sets of points: 250 and 500. We plot the variation
of (m,  ) and (s, c) with
) and (s, c) with 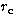 for these 2 sets of points in
Fig. 2 for the King profiles. The parameters vary significantly with
for these 2 sets of points in
Fig. 2 for the King profiles. The parameters vary significantly with 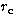 at the 3
at the 3  level. The size of the errors are similar to those for
the Poisson case: very small for (m,
level. The size of the errors are similar to those for
the Poisson case: very small for (m,  ), median for s and very large
for c. The parameters (m,
), median for s and very large
for c. The parameters (m,  ) are not significantly different from the
Poisson case for large characteristic radii (
) are not significantly different from the
Poisson case for large characteristic radii (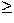 225 kpc). The
skewness is significantly different at the 1
225 kpc). The
skewness is significantly different at the 1  level from the
Poisson case whatever the characteristic radius. The mean value of the
curtosis is also different, but not significantly because of the large error
bars.
level from the
Poisson case whatever the characteristic radius. The mean value of the
curtosis is also different, but not significantly because of the large error
bars.
![\begin{figure}
\includegraphics[angle=-90,width=17cm,clip]{fig3.ps}\end{figure}](/articles/aas/full/1999/02/ds7993/Timg19.gif) |
Figure 3:
Variation with the characteristic radius of the NFW distribution
of: upper left: (m,  ) and 250 points (the increasing line is m and the
decreasing line is ) and 250 points (the increasing line is m and the
decreasing line is  ), upper right: (s, c) and 250 points (s is the
line with error bars and c is the line without error bar), lower left:
(m, ), upper right: (s, c) and 250 points (s is the
line with error bars and c is the line without error bar), lower left:
(m,  ) and 500 points (the increasing line is m and the decreasing line
is ) and 500 points (the increasing line is m and the decreasing line
is  ), lower right: (s, c) and 500 points (s is the line with error
bars and c is the line without error bar) ), lower right: (s, c) and 500 points (s is the line with error
bars and c is the line without error bar) |
In Fig. 3 we plot the variations for the NFW profiles and the trends are
very different. All the parameters (m,  , s, c) differ significantly at the
1
, s, c) differ significantly at the
1  level from the Poisson case. We also notice an important
degeneracy between m and
level from the Poisson case. We also notice an important
degeneracy between m and  .
.
We want to determine a parameter based on m,  , s and c which is able
to discriminate the three profiles. We want to test
the distance in a n dimensional space with n=2, if we use (m,
, s and c which is able
to discriminate the three profiles. We want to test
the distance in a n dimensional space with n=2, if we use (m,  ), n=3
if we use (m,
), n=3
if we use (m,  , s) and n=4 if we use (m,
, s) and n=4 if we use (m,  , s, c). More
generally, the distance in a space of n dimensions between (p1, p2,
..., pn) and (q1, q2, ..., qn) is
, s, c). More
generally, the distance in a space of n dimensions between (p1, p2,
..., pn) and (q1, q2, ..., qn) is
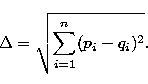
The error on a such distance is calculated by derivation:
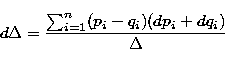
where dpi and dqi are the errors on pi and qi.
Therefore, we define three distances: 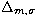 ,
,
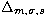 , and
, and 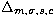 .
.
We calculate these distances for the Poisson distribution and the King
and the NFW profiles for 3 different sets of points (50, 125 and 500) and
for all characteristic radii. We plot (with errors) in Figs. 4, 5 and 6 these
distances as a variation of the
characteristic radius. We symbolize the null distance as a solid line and we
plot the errors on the determination of the parameters of the Poisson distributions.
![\begin{figure}
\includegraphics[angle=-90,width=17cm,clip]{fig4.ps}\end{figure}](/articles/aas/full/1999/02/ds7993/Timg25.gif) |
Figure 4:
Variation with the characteristic radius of the 3 tested distances
between the Poisson and the King distribution (crosses) and the Poisson
and the NFW distribution (circles). We have 50 points in the samples.
We plot the error bar on each points and we symbolize the error on the
parameters of the Poisson distribution with the two horizontal dashed lines.
The horizontal solid line symbolizes the null distance to the Poisson distribution.
The left part of the figure is for the distance 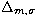 , the
lower right part is for , the
lower right part is for 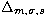 and the upper right part is
for and the upper right part is
for 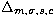 |
![\begin{figure}
\includegraphics[angle=-90,width=17cm,clip]{fig5.ps}\end{figure}](/articles/aas/full/1999/02/ds7993/Timg26.gif) |
Figure 5:
Variation with the characteristic radius of the 3 tested distances
between the Poisson and the King distribution (crosses) and the Poisson
and the NFW distribution (circles). We have 125 points in the samples.
We plot the error bar on each points and we symbolize the error on the
parameters of the Poisson distribution with the two horizontal dashed lines.
The horizontal solid line symbolizes the nul distance to the Poisson distribution.
The left part of the figure is for the distance 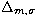 , the
lower right part is for , the
lower right part is for 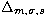 and the upper right part is
for and the upper right part is
for 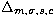 |
![\begin{figure}
\includegraphics[angle=-90,width=17cm,clip]{fig6.ps}\end{figure}](/articles/aas/full/1999/02/ds7993/Timg27.gif) |
Figure 6:
Variation with the characteristic radius of the 3 tested distances
between the Poisson and the King distribution (crosses) and the Poisson
and the NFW distribution (circles). We have 500 points in the samples.
We plot the error bar on each points and we symbolize the error on the
parameters of the Poisson distribution with the two horizontal dashed lines.
The horizontal solid line symbolizes the nul distance to the Poisson distribution.
The left part of the figure is for the distance 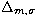 , the
lower right part is for , the
lower right part is for 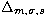 and the upper right part is
for and the upper right part is
for 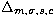 |
From these figures, we notice the following:
- First of all, the difference between the Poisson distribution and King and NFW profiles increases with the
number of points.
- For 50 points, we have much confusion between the King and NFW profiles,
as well as with the
Poisson distribution whatever the distance used. It is impossible to characterize
the distributions of 50 points.
- For 125 or 500 points,
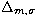 is significant at the 1
is significant at the 1
 level between the three profiles. Unfortunately, the values of
level between the three profiles. Unfortunately, the values of
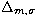 are very low (more than 60% lower) compared, for
example, to the distance between the point (m=0,
are very low (more than 60% lower) compared, for
example, to the distance between the point (m=0, 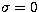 ) and the Poisson
distribution. So, the use of
) and the Poisson
distribution. So, the use of 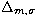 is not straightforward.
is not straightforward.
- For 125 and 500 points
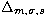 is significant at the
same level, except
between a King profile with
is significant at the
same level, except
between a King profile with 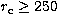 (and 125 objects) and a
Poisson distribution, and
between the King profiles with very low characteristic radii and the NFW
profiles with very high characteristic radii.
(and 125 objects) and a
Poisson distribution, and
between the King profiles with very low characteristic radii and the NFW
profiles with very high characteristic radii.
The values of 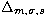 are higher than those of
are higher than those of 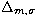 : 400% higher compared to the distance between the point
(m=0,
: 400% higher compared to the distance between the point
(m=0, 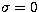 ) and the Poisson distribution. The high values and the low
confusions induced by this distance are able to discriminate efficiently the
3 profiles. We see a continuous variation of the distance from the Poisson
distributions to the more cusped ones.
) and the Poisson distribution. The high values and the low
confusions induced by this distance are able to discriminate efficiently the
3 profiles. We see a continuous variation of the distance from the Poisson
distributions to the more cusped ones.
- For 125 and 500 points,
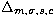 has high values,
but the very large error bars on each parameters induce many confusions
between the King and the NFW profiles (even if the distances with the
Poisson distribution are significant). So,
has high values,
but the very large error bars on each parameters induce many confusions
between the King and the NFW profiles (even if the distances with the
Poisson distribution are significant). So, 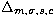 is not the best
distance.
is not the best
distance.
We therefore choose 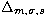 to discriminate between the
aggregation degree of a set of points. The limiting factor is a number of objects
greater than 125. We note here that, whatever the used distance, we are not
able to discriminate between different characteristic radii for a given
profile, but this is not the goal of this work. The NFW profiles are more
distant to the Poisson distributions than the King ones (whatever
the characteristic radius). According to the cusped and non-cusped shape of
the NFW and King profiles, we can say that the sets of points (with a given
number of points) with a great distance
to discriminate between the
aggregation degree of a set of points. The limiting factor is a number of objects
greater than 125. We note here that, whatever the used distance, we are not
able to discriminate between different characteristic radii for a given
profile, but this is not the goal of this work. The NFW profiles are more
distant to the Poisson distributions than the King ones (whatever
the characteristic radius). According to the cusped and non-cusped shape of
the NFW and King profiles, we can say that the sets of points (with a given
number of points) with a great distance 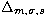 compared to a
Poisson distribution with the same number of points, are more concentrated
than those ones with a low
compared to a
Poisson distribution with the same number of points, are more concentrated
than those ones with a low 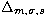 .
.


Up: The use of minimal distribution
Copyright The European Southern Observatory (ESO)
![]() are used. These two parameters are efficient for a Gaussian
distribution. To
characterize some non Gaussian distributions, we have to use more advanced
momenta like the skewness s and/or the curtosis c. We have tested the use of
these parameters in the following. Below, we describe the methodology:
are used. These two parameters are efficient for a Gaussian
distribution. To
characterize some non Gaussian distributions, we have to use more advanced
momenta like the skewness s and/or the curtosis c. We have tested the use of
these parameters in the following. Below, we describe the methodology:
![]() . So,
we divide all the length by this factor (where S is the area of the maximum
rectangle of the point set). We calculate finally the mean m, the dispersion
. So,
we divide all the length by this factor (where S is the area of the maximum
rectangle of the point set). We calculate finally the mean m, the dispersion
![]() , the skewness s and the curtosis c of H.
, the skewness s and the curtosis c of H.
![]() is the density
and r the radius, we have:
is the density
and r the radius, we have:
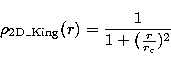
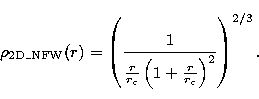
![]() , s, c. From these data, we
are able to compute the mean value and the dispersion of each parameter m,
, s, c. From these data, we
are able to compute the mean value and the dispersion of each parameter m,
![]() , s or c.
, s or c.
![\begin{figure}
\includegraphics[angle=-90,width=8.8cm,clip]{fig1.ps}\end{figure}](/articles/aas/full/1999/02/ds7993/Timg10.gif)
![]() are asymptotically equal to 0.66
are asymptotically equal to 0.66 ![]() 0.02
and 0.31
0.02
and 0.31 ![]() 0.02 in perfect agreement with Dussert (1988). The error bars
are 3% of the mean value. The final value is reached for a number N of points
in the simulation greater than 125.
0.02 in perfect agreement with Dussert (1988). The error bars
are 3% of the mean value. The final value is reached for a number N of points
in the simulation greater than 125.
![]() with a final value of
0.29
with a final value of
0.29 ![]() 0.14. The errors are greater: about 50% of the mean value.
0.14. The errors are greater: about 50% of the mean value.
![]() with very large error
bars (
with very large error
bars (![]() 100% of the mean value). The final value is 0.33.
100% of the mean value). The final value is 0.33.
![]() , s, c)
for different characteristic radii
, s, c)
for different characteristic radii ![]() of
King and NFW profiles. We use
of
King and NFW profiles. We use ![]() , 75, 100, 125, 150, 175, 200, 225,
250, 275 and 300 kpc. For a given profile and a given characteristic
radius, we simulate 2 sets of points: 250 and 500. We plot the variation
of (m,
, 75, 100, 125, 150, 175, 200, 225,
250, 275 and 300 kpc. For a given profile and a given characteristic
radius, we simulate 2 sets of points: 250 and 500. We plot the variation
of (m, ![]() ) and (s, c) with
) and (s, c) with ![]() for these 2 sets of points in
Fig. 2 for the King profiles. The parameters vary significantly with
for these 2 sets of points in
Fig. 2 for the King profiles. The parameters vary significantly with ![]() at the 3
at the 3 ![]() level. The size of the errors are similar to those for
the Poisson case: very small for (m,
level. The size of the errors are similar to those for
the Poisson case: very small for (m, ![]() ), median for s and very large
for c. The parameters (m,
), median for s and very large
for c. The parameters (m, ![]() ) are not significantly different from the
Poisson case for large characteristic radii (
) are not significantly different from the
Poisson case for large characteristic radii (![]() 225 kpc). The
skewness is significantly different at the 1
225 kpc). The
skewness is significantly different at the 1 ![]() level from the
Poisson case whatever the characteristic radius. The mean value of the
curtosis is also different, but not significantly because of the large error
bars.
level from the
Poisson case whatever the characteristic radius. The mean value of the
curtosis is also different, but not significantly because of the large error
bars.
![]() , s, c) differ significantly at the
1
, s, c) differ significantly at the
1 ![]() level from the Poisson case. We also notice an important
degeneracy between m and
level from the Poisson case. We also notice an important
degeneracy between m and ![]() .
.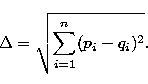
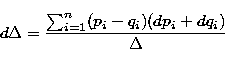
![]() ,
,
![]() , and
, and ![]() .
.![]() are higher than those of
are higher than those of ![]() : 400% higher compared to the distance between the point
(m=0,
: 400% higher compared to the distance between the point
(m=0, ![]() ) and the Poisson distribution. The high values and the low
confusions induced by this distance are able to discriminate efficiently the
3 profiles. We see a continuous variation of the distance from the Poisson
distributions to the more cusped ones.
) and the Poisson distribution. The high values and the low
confusions induced by this distance are able to discriminate efficiently the
3 profiles. We see a continuous variation of the distance from the Poisson
distributions to the more cusped ones.