Hodge (1978) identified twenty OB associations concentrated primarily in the
core of the galaxy with a mean diameter of 164 pc. Freedman (1988a) presented
color-magnitude diagrams for 11 of them and gave some age estimates using
period-age relations for Cepheids. In our field of observations we have 9 of
the Hodge associations - Nos. 10, 11, 12, 13, 14, 15, 17, 18 and No. 19. Figure
11 shows the (![]() ) color-magnitude diagrams of the Hodge associations. The
new plot of color-magnitudes diagrams shows well-defined main sequences with
widths of typically 0.2, blue and red supergiants in A10, A11 and A14 and some
intermediate age stars and red giant stars.
) color-magnitude diagrams of the Hodge associations. The
new plot of color-magnitudes diagrams shows well-defined main sequences with
widths of typically 0.2, blue and red supergiants in A10, A11 and A14 and some
intermediate age stars and red giant stars.
![\begin{figure}
\includegraphics [clip,height=18cm]{ds7636f11.eps}\end{figure}](/articles/aas/full/1999/01/ds7636/Timg41.gif) |
Figure 11:
|
Figure 12 and Fig. 13 show the comparison with the isochrones from Padua's
library (see Bertelli et al. 1994) and a (Log![]() )diagram. They were built in the same manner as in the previous section.
)diagram. They were built in the same manner as in the previous section.
![\begin{figure}
\includegraphics [clip,height=18cm]{ds7636f12.eps}\end{figure}](/articles/aas/full/1999/01/ds7636/Timg42.gif) |
Figure 12: ((V-B)0, MV) color-magnitude diagrams for Hodge associations. Isochrones from Padua's library with z=0.004 are superimposed |
On the assumption that all the stars in each association have the same age we can determine the age of the associations following the method of Flannery & Johnson (1982). The distance of the star j of the association to a given isochrone was computed as:
![\begin{displaymath}
\textstyle d_j^2 = MIN _{i=1,\ldots ,n}\left [\left (\frac{V...
...eft (\frac{(B-V)_j-(B-V)_i}{\sigma_{(B-V)_j}}\right )^2\right ]\end{displaymath}](/articles/aas/full/1999/01/ds7636/img43.gif)
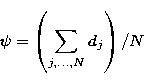
As can be seen in Fig. 12 there are some yellow and red stars in all
associations, which have ages between 100 and 300 Myr. In the theoretical H-R
diagram (Fig. 13) they lie between 4 and 7 ![]() . We consider one small
part of them to be field stars from our Galaxy (according to Table 3 in V
< 21 mag the expected number of field stars is approximately 30) and the rest
to be field stars from IC1613. To investigate the behavior of
foreground stars we selected the "comparison field area" with the same mean
diameter as the Hodge association - 164 pc and far from any known association.
The color-magnitude diagram, the isochrone comparison and the H-R diagram were
built in the same way as in the associations and are shown in Fig. 14. As can
be easily seen except for a few faint blue stars that lie on the main sequence
most stars are faint, low-mass and 100 - 300 Myrs old.
. We consider one small
part of them to be field stars from our Galaxy (according to Table 3 in V
< 21 mag the expected number of field stars is approximately 30) and the rest
to be field stars from IC1613. To investigate the behavior of
foreground stars we selected the "comparison field area" with the same mean
diameter as the Hodge association - 164 pc and far from any known association.
The color-magnitude diagram, the isochrone comparison and the H-R diagram were
built in the same way as in the associations and are shown in Fig. 14. As can
be easily seen except for a few faint blue stars that lie on the main sequence
most stars are faint, low-mass and 100 - 300 Myrs old.
In the upper part of the theoretical H-R diagram (masses ![]() ,Fig. 13) most of the associations except A12, A18 and A19 contain young
massive stars which have been born almost coeval. Following Massey et al.
(1995) we tabulated the most massive stars still present in the associations in
Table 5. The masses of the most massive stars are listed in Col. 3 and Col. 4
contains a number of stars with masses higher than
,Fig. 13) most of the associations except A12, A18 and A19 contain young
massive stars which have been born almost coeval. Following Massey et al.
(1995) we tabulated the most massive stars still present in the associations in
Table 5. The masses of the most massive stars are listed in Col. 3 and Col. 4
contains a number of stars with masses higher than ![]() . The
analysis of Table 5 shows that the associations containing the most massive
stars are the youngest ones while the associations containing only low-mass
stars are indeed the oldest.
. The
analysis of Table 5 shows that the associations containing the most massive
stars are the youngest ones while the associations containing only low-mass
stars are indeed the oldest.
Hodge (1978) included the brightest red supergiants V32 and V38 in the
boundaries of A10 and A14. According to the paper of Massey (1998) they could
be real members of those associations. V32 and V38 stand around ![]() (Fig. 13) and have very high
(Fig. 13) and have very high ![]() -9.84 and -9.70 respectively. On
the other hand the age of both A10 and A14 is
-9.84 and -9.70 respectively. On
the other hand the age of both A10 and A14 is ![]() Myr. As Massey (1998)
mentioned. "At 5 Myr we would find only WN stars and few if any RSGs, and at 7
Myr we would find only RSGs". The comparison with the masses and
Myr. As Massey (1998)
mentioned. "At 5 Myr we would find only WN stars and few if any RSGs, and at 7
Myr we would find only RSGs". The comparison with the masses and ![]() of
the red supergaints in M31, M33 and NGC6822 given by Massey (1998) shows
that the two supergaints in IC1613 are similar to the red supergaints in
NGC6822.
of
the red supergaints in M31, M33 and NGC6822 given by Massey (1998) shows
that the two supergaints in IC1613 are similar to the red supergaints in
NGC6822.
![\begin{figure}
\includegraphics [clip,height=18cm]{ds7636f13.eps}\end{figure}](/articles/aas/full/1999/01/ds7636/Timg54.gif) |
Figure 13: Theoretical H-R diagrams for Hodge associations Nos. 10, 11, 12, 13, 14, 15, 17, 18 and No. 19 |
![\begin{figure}
\includegraphics [clip,height=9.5cm]{ds7636f14.eps}\end{figure}](/articles/aas/full/1999/01/ds7636/Timg55.gif) |
Figure 14: The color-magnitude diagram, the isochrone comparison and the H-R diagram of the "comparison field area" with mean diameter 164 pc |
Three Wolf-Rayet (WR) stars reported by Armandroff & Massey (1985) -- WR4, WR5 and WR8 are in our field of observations. These stars belong to the associations A10, A13 and A14 respectively and have following magnitudes and colors: WR4 -- V=19.16, U-B= -0.39, B-V=-0.41; WR5 -- V=20.78, U-B= -1.00, B-V=-0.27; WR8 -- V=19.56, U-B= -1.80, B-V=0.53. The WR8 is embedded in the supernova remnant S8 (Peimbert et al. 1988), which lead to the very unrealistic magnitude and colors. The presents of the WR stars in A10, A13 and A14 is in good agreement with youngest age of these associations.
It is not possible to calculate the IMF for each association because
of small association members and therefore large statistical errors. In order
to improve the statistics we summarized Hodge associations in three groups.
First group contains the blue stars from A10, A11, A14 and A17 (having ages
between 5-8 Myr), second group contains A13 and A15 (having age 10 Myr) and
the last one contains the stars from A12, A18 and A19 (with age 20 Myr).
The slopes of IMFs for these three groups are ![]() ,
,![]() and
and ![]() respectively.
The uncertainty in the slope is the uncertainty in the least-squares fit to
the IMF. According to Fabry Pérot images (Rosado 1998) the stars from
the first group of Hodge associations are embedded into shells of gas, while
there is not any gas in the last association group (A12, A18 and A19).
respectively.
The uncertainty in the slope is the uncertainty in the least-squares fit to
the IMF. According to Fabry Pérot images (Rosado 1998) the stars from
the first group of Hodge associations are embedded into shells of gas, while
there is not any gas in the last association group (A12, A18 and A19).
The different stellar content, age differences, variations of slopes of IMFs and presence of gas into some of associations, show a signature of a presence of two waves of star formation.
The stellar associations were identified by Hodge (1978) by eye estimation. The
present criterion is the objective determination of the boundaries of OB
associations. It suggests that OB stars should be assigned to one and the same
stellar association if they have a statistically significant peak of surface
stellar density above the mean level of the surrounding OB stars. The OB
associations are groups with the highest stellar density. The neighbour
distances between the stars inside the associations are substantially smaller
than those of the background ones outside the association. The mean value of
the distance to the nearest neighbour in an OB association is a measure for
stellar density (see Appendix in Ivanov 1996). The stellar density function in
the association is defined as ![]() , for
, for ![]() ,where N is the number of candidate OB associations in the galaxy. A reliable
function for statistical evaluation of the possible maximal density of the N
stellar groups is the Fourier transform of the function
,where N is the number of candidate OB associations in the galaxy. A reliable
function for statistical evaluation of the possible maximal density of the N
stellar groups is the Fourier transform of the function ![]() for
the different candidates for OB associations:
for
the different candidates for OB associations:
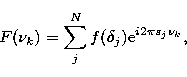 |
(1) |
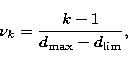 |
(2) |
The amplitude of the Fourier transform is:
![\begin{eqnarray}
FF(\nu_k) &=& \frac {1} {N} \left \{ \left [ \sum _j^N f(\delta...
...j^N f (\delta_j)\sin (2\pi s_j \nu_k) \right ]^2 \right \}^{1/2} .\end{eqnarray}](/articles/aas/full/1999/01/ds7636/img67.gif) |
||
| (3) |
These parameters select the smallest groups in IC1613 with a mean size
(![]() ) 60 pc. These 30 groups have the smallest size in the hierarchy of
OB stellar groups but they have the highest stellar density in IC1613.
) 60 pc. These 30 groups have the smallest size in the hierarchy of
OB stellar groups but they have the highest stellar density in IC1613.
Following the present criterion we select relatively small groups with high stellar density which is at least 4 times higher than that of the surrounding OB stars. However the mean stellar density of the 30 selected groups is 35 times above the background OB stars.
The re-determined OB associations are shown in Table 6. Column 1 gives the number of the group, Cols. 2 and 3 give the mean coordinates of the group in pixels, Col. 4 gives the average size of the group in pc, Col. 5 gives the number of member stars and column 6 gives the mean stellar density. A map of the new associations is shown in Fig. 15.
Most of the stellar associations outlined by Hodge coincide with our groups but the present criterion divides Hodge's associations into several smaller groups. They look like bright cores within Hodge's associations. The present criterion selects a core structure of OB stars in the classic associations. They are probably the youngest OB stars in the associations. It is known that young associations in the Galaxy like Trapezium contain small compact subgroups similar to those selected by the present criterion in IC1613 while the older associations consist of randomly distributed stars and they could not be divided into subgroups. Using the present criterion we identified 30 small groups of OB stars with a mean size of about 60 pc. Hodge (1986) describes the problem of the different sizes of the stellar associations in the Magellanic clouds and other nearby galaxies as M31 and M33. He concluded that the mean size of the associations depends on the plate scale and the distance to the galaxy. The present criterion is very strong, the result being that only the youngest associations are identified. This may explain the smaller mean size of the stellar groups identified in the present paper than those presented by Hodge (1986).
![\begin{figure}
\includegraphics [clip,height=8.6cm]{ds7636f15.eps}\end{figure}](/articles/aas/full/1999/01/ds7636/Timg74.gif) |
Figure 15: Observational area for IC1613 with superimposed boundaries of new associations. The two new open cluster candidates are marked by dashed line.North is on top, East is to the left |
Copyright The European Southern Observatory (ESO)