3 Error analysis and completeness

3.1 Photometric errors

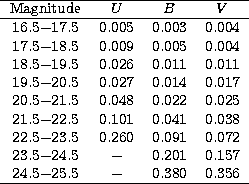
In order to estimate the internal accuracy of our CCD measurements we used the formal errors from the DAOPHOT package and as additional error estimates we used the magnitude differences from experiments with artificial stars. Table 1 lists the derived average standard deviations for successive intervals of one magnitude in the U, B and V frames. As can be seen we have large errors (>0.15) at the faint magnitudes: U > 22.5, B > 23.5 and V > 24.0. The standard errors from all stars vs. magnitude are displayed in Fig. 3.

 

Table 1: The mean standard deviations

  

Figure 3: Internal errors of the CCD photometry

The artificial star simulations necessary for the completeness correction can also be used to determine the measurement errors. A set of artificial stars randomly placed on the original frames were re-determined in the same manner as the program stars. The "input-output" differences in B and V magnitudes between "added" and "recovered" artificial stars as a function of the measured output magnitude are shown in Fig. 4. The mean errors of the "input-output" differences in B and V magnitudes are 0.025 and 0.024 respectively.

  

Figure 4: The "input-output" differences in B and V magnitudes as a function of the measured output magnitude

3.2 Completeness correction

The last step in our data reductions was to determine the completeness functions in the B and V filters. We used the artificial star technique (Stetson & Harris 1988; Stetson 1991) creating series of artificial frames by means of the ADDSTAR routine in DAOPHOT II which were re-reduced in the same manner as the original frames. The completeness correction derived as the ratio of added to recovered artificial stars was then fitted by a cubic spline. The completeness function is listed in Table 2. We consider our sample complete up to 22.5 mag in both B and V filters. In Cols. 4 and 5 as independent completeness estimation the magnitude distributions for the stars in U and V filter binned by 0.5 are given. The turnover interval in U filter is at U=21.5 mag which we will consider as a completeness limit in this filter. The completeness magnitudes in B and V agree with the values determined by artificial stars.

  

Table 2: Completeness function

3.3 Field star contamination

It is obviously necessary to check the level of field star contamination in the color magnitude diagram before discussing its detailed structure. Based on the Bahcall & Soneira (1980) model of the Galaxy, Ratnatunga & Bahcall (1985) have predicted the field star densities in the direction of IC1613. Table 3 gives the number of objects expected per bin of magnitude and color in the area covered by our observations. In summary the total number of expected field stars in our field is 47, while we can expect approximately two stars brighter than 19 mag in V and (B-V) < 0.8. Field stars therefore should not seriously affect the structure of the CMD and no corrections for field contamination have been applied to the IC1613 data.

 

Table 3: Expected numbers of field stars towards IC1613