A detailed analysis of the O-C diagrams of ensemble of semi-detached binaries which contain only stars with radiative outer layers was performed. The summary of results can be found in Table 5. The periods are constant, or display only monotonic changes, in the intervals covered by the timings. These intervals are several decades long (even more than 70 years in most cases). With one exception no signs of complicated course were detected in the O-C diagrams of the respective systems within the covered intervals. In only one case, TT Aur, the course of the period changes appears more complex but the cyclic term and its parameters can be well explained in terms of LITE. This detailed analysis brought further evidences that the period changes in ET-systems really have significantly less complicated course than in LL-Algols and the finding of Hall (1989) was thus confirmed. These results, that is absence of alternate period changes in ET-systems, strengthen the evidence for an important role of the outer convective layer of a component of a binary in the period changes of LL-Algols.

**Table 5:** Summary of changes of the orbital periods in the binaries with purely early-type components. The rate of change of the orbital period $\Delta$ P/P is given in days $^{\rm -1}$ . Significance S of the period change is defined in the text; the larger S, the better defined variation
$\begin{tabular} {lcl} \hline Binary & $S$\space & Period~changes \\ \hline V337 ... ...ses: parabolic course $\Delta$$P/P= 2.87\ 10^{-10}$\space \\ \hline\end{tabular}$

There were accumulated evidences that many period changes in LL-Algols have character of episodes of abrupt changes (completed within less than a year) which are separated by intervals several years long during which the period length remains almost constant (e.g. U Cep - Olson et al. 1981, RR Dra - Pokorný & Zlatuska 1976). The typical value of the period change in a single episode in LL-Algols is $\Delta$ $P/P\approx 10^{-5}$ days $^{\rm -1}$ . These episodes can be even grouped into seasons of enhanced activity (RW Tau - Simon 1997c) and the underlying mechanism may be found in the structure changes of the late-type loser with COL. Unfortunately, the available data analysed here do not resolve the character of the course of the period changes in ET-systems in detail. The possibility of abrupt change was discussed in several ET-systems in the present analysis (BF Aur, Z Vul, XZ Cep, SX Aur). The data would suggest only one episode inside the interval several decades long. Nevertheless, the abrupt changes are hardly resolvable from the smooth course in the available data. The polynomial fits to the O-C values of the respective ET-systems have shown that even the most variable periods could be plausibly matched by the second order polynomials and can be treated as smooth. We can only state that if these changes are really abrupt then the typical corresponding value of $\Delta$ P/P is about $2\ 10^{-6}$ days $^{\rm -1}$ , that is lower than in LL-Algols.

Now we will turn to the mechanisms which can lead to the monotonic period changes in ET-systems and search for their possible contribution to the observed variations. Two basic groups of mechanisms can be established: (i) mass transfer and/or mass loss from the system; (ii) changes of the rotational angular momenta of the components.

As the semi-detached configuration implies these ET-systems are a result of the mass exchange and this transfer still continues at least in some of them. The binary begins its mass transfer epoch with q>1 and its value decreases in the course of the subsequent evolution. The models show that the largest $\dot m$ occurs in the early phase of the transfer and decreases afterwards. It means that less evolved systems should in principle possess larger period changes. As was shown above (Figs. 18 and 17) this trend is really apparent in the close systems with P<7 days.

Another less numerous group of wider systems with significantly longer orbital periods ( $\beta$ Lyr, RY Sct and AQ Cas) can be resolved in Fig. 17ab. Two of these systems, $\beta$ Lyr and RY Sct, possess the largest absolute magnitudes of the period changes in the set analysed here (Fig. 18), despite of their low values of $q\approx0.3$ . In the same way, these two binaries display very strong photometric and spectroscopic activity connected with the large-scale mass transfer. This transfer gives rise to a huge accretion disk completely veiling the gainer in $\beta$ Lyr (and probably also in RY Sct). The high value of $\dot m$ in $\beta$ Lyr, determined from the period changes by Harmanec & Scholz (1993), acceptably agrees with that determined from the model of the disk (Hubený & Plavec 1991) and the connection of the period change with the mass transfer appears to be well established. The huge mass loss rate from RY Sct determined from the radio data is $\dot m_{\rm loss}= 6\ 10^{-5}~M_{\odot}~{\rm yr}^{-1}$ (Milano et al. 1981). RY Sct is the only one system of this set in which the period decrease is clearly present. An explanation for this decrease can be offered in terms of the intermediate mode (Huang 1963) when the outflowing matter forms a circumbinary ring removing angular momentum from the system. In this case it is necessary to find a mechanism which forces the matter to escape from the binary and form the ring. The radiative force of the early-type components is worthy consideration. The evaluation of the influence of this force on the Roche geometry of the respective ET-systems was carried out using the approach of Huang & Taam (1990). They made use of the coefficients a₁, a₂ which characterize the efficiency of the radiative force with respect to the gravity. Values of a₁, a₂ are in the range from 0 (no radiative force) to 1 (radiative force just balances the gravity force). Although the uncertainty of the parameters of RY Sct may be appreciable the values of a₁, a₂ for both stars of this system are several tenths, which is more than an order of magnitude larger than for the rest systems (with the exception of V 448 Cyg and XZ Cep). As can be seen from the model by Huang & Taam (1990) such a large value of a₁, a₂ may alter the Roche geometry. In an extreme case one of the lobes can open while the L₁ point is secured. Although Huang and Taam argued that the effect of radiation becomes reduced in the case when a star occupy a large part of its lobe the role of the exceptionally strong radiative field in RY Sct seems to offer at least a tentative explanation for the large mass loss rate and consequently the rate of the period decrease observed.

As for AQ Cas, its physical and geometric parameters are very similar to $\beta$ Lyr but its activity is significantly lower. Both stars of AQ Cas are directly visible (Olson 1994) and there is not any sign of a huge accretion disk. The constant period of AQ Cas can be then explained by a much smaller $\dot m$ in comparison with $\beta$ Lyr.

The above mentioned difference between the groups of the short and long-period ET-systems can be clarified if the different evolutionary modes are taken into account. Case A operates for systems with the initial periods of the order of a day while wider binaries evolve through case B. As the models show (e.g. Pols 1994) the evolution through case B leads to a lower value of q than in case A and, moreover, since the duration of the mass transfer epoch for case B is significantly shorter than in case A it will give rise to higher mass transfer rate and consequently a larger period change can be expected. The analysis of the evolutionary status is available for several ET-systems. SX Aur, DM Per, u Her are probably products of case A while $\beta$ Lyr, RZ Sct, V 356 Sgr (and possibly Z Vul) evolve through case B (Giuricin & Mardirossian 1981b). The evolution of $\beta$ Lyr and V 356 Sgr through case B was also confirmed by the models of Ziolkowski (1976 and 1985). Harries et al. (1997) preferred case B for XZ Cep and V 448 Cyg. When these evolutionary scenarios are compared with the diagrams in Figs. 17 and 18 we find that the only systems evolving through case A in which the period changes are detected are binaries with still quite high q (SX Aur and TT Aur). The rest evolved systems possessing period change are of case B ( $\beta$ Lyr, XZ Cep, Z Vul).

Not only the mass ratio but also the mass of the loser plays a role in the period changes. It can be inferred from the densely populated interval of masses $1.5 - 8~M_{\odot}$ in the mass-luminosity diagram (Fig. 19). The systems (apart from BF Aur) are after the phase of rapid mass transfer (because of their clearly reversed q) and the luminosity of the losers is therefore expected to grow again. These stars then move in an approximately parallel direction in Fig. 19, i.e. towards smaller masses and higher luminosities. The distribution of systems in this figure may therefore reflect a division between the evolution of the losers of lower and higher mass to some extent. The systems with the components of higher mass evolve faster and possess higher $\dot m$ .

In the light of the evidences discussed above it is tempting to understand the observed period changes in ET-systems as consequences of the mass transfer. If the period in the evolved systems with q<1 is variable then we observe its increase in those systems in which the radiative forces are negligible. In this interpretation the increase of P may be reconciled with the dominant conservative mode. A possible contribution of the Jeans mode (matter escaping from the system at a high speed; Huang 1963) cannot be separated since it prolongs the orbital period, too. The dominant intermediate mode, leading to the period decrease, is supposed only in the high-luminosity RY Sct in which the radiative forces are strong.

However, the case of the period change in BF Aur, although well documented, cannot be decided at present. The available solutions do not give unique configuration and it is not possible to identify the loser and gainer unambiguously. It cannot be even ruled out that BF Aur is still before the onset of the mass transfer epoch. In the framework of the model of Demircan et al. (1997) the increase of the period length may be attributed to the dominant conservative mode. Since the value of the observed $\Delta$ P/P in this mode goes to zero as $q\rightarrow1$ then even high $\dot m$ can lead just to marginal period change in BF Aur.

Although possible colliding winds in BF Aur were inferred from the photometry by Kallrath & Kamper (1992) they are unlikely to be the cause of the observed change since even for the pure Jeans mode very large $\dot m_{\rm loss}\approx 2\ 10^{-7}M_{\odot}~{\rm yr}^{-1}$ would be needed.

It is interesting to determine at least an order of magnitude value of the mass transfer rate for the conservative case (which allows to keep the number of free parameters as low as possible) to get an idea of $\dot m$ which can be derived from the observed O-C changes (Huang 1963). The rate of the period change $\Delta P$ /P for this mode can be expressed as

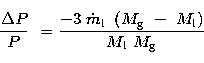$\begin{displaymath} \frac{{\Delta P}}{P}~= \frac{-3~\dot m_{\rm l}~\left(M_{\rm g}~-~M_{\rm l}\right)}{M_{\rm l}~M_{\rm g}}\end{displaymath}$

(14)

where $M_{\rm g}$ and $M_{\rm l}$ are masses of the gainer and loser, respectively, and $\dot m_{\rm l}$ denotes the mass transfer rate per orbital cycle. The values of $\dot m$ in $M_{\odot}~{\rm yr}^{-1}$ for the evolved systems (q<1) which display period increase were obtained using Eq. (14) and are given in Table 6. It can be seen that the lower limit for which the period change can be recognized from the data is about $6\ 10^{-8}~M_{\odot}~{\rm yr}^{-1}$ . Such a value is consistent with the phase of slow mass transfer and implies that generally the period changes of this magnitude, corresponding to the advanced evolutionary phase of a system, should be still revealed if they were indeed present. A direct comparison of the values from Table 6 with $\dot m$ determined from the observations of the circumstellar matter is difficult because as the position in the r-q diagram suggests there is only little room left in the lobe of the gainer in most these systems (apart from $\beta$ Lyr-see above). It should be noted that the period changes produced by the mass transfer rates obtained here (apart from $\beta$ Lyr) would be easily overlapped by the activity of the late-type component in LL-Algols.

**Table 6:** The mass transfer rate determined from the observed period changes assuming the conservative mode
$\begin{tabular} {lcl} \hline \noalign{\smallskip} Binary & & $\dot m$\space ($M_... ... & $3.4\ 10^{-5}$\space \\ Z~Vul & & $5.7\ 10^{-8}$\space \\ \hline\end{tabular}$

Two systems, AQ Cas and RZ Sct, for which the mass transfer rates $\dot m$ (about $5\ 10^{-7}M_{\odot}~{\rm yr}^{-1}$ ) determined by Olson & Bell (1989) from the photometric manifestations of the mass stream are available enabled a comparison of the expected period changes with the observed ones. The conservative transfer was used for this comparison (Figs. 6 and 14) and although this approach is an idealization it is useful as the first step since it does not require free parameters. The O-C values of AQ Cas are consistent with the constant period (within the scatter) while the corresponding increase of the period length is possible in RZ Sct. Nevertheless, the scatter of the available timings precludes definite conclusion and new photoelectric data are urgently needed here.

The influence of the magnetic activity which is supposed to be strong in cool stars with COL and which can be the cause of the alternate period changes (Hall 1989; Applegate 1992) is missing in ET-systems. Also differences of the internal structure of the late and early-type stars can play a role because they affect the constant of the apsidal motion k₂₂. Changes of k₂₂ can give rise to variations of P (Matese & Whitmire 1983) and the larger value of k₂₂, the larger its contribution to the possible period changes. k₂₂ is very sensitive to the density profile $\rho(r)$ . As the calculations of the contributions of the respective parts of a star to k₂₂, presented by Petrova (1995), showed k₂₂ is governed namely by the layers within which 0.9 of the total mass of the star is contained. The decrease of the density with the radius in the radiative outer layers of the early-type stars is more rapid than in the late-type stars with COL (to which the losers in LL-Algols belong). It implies that 0.9 mass is contained within a significantly smaller fractional radius in the early-type stars and hence these stars possess smaller k₂₂ in comparison with the late-stars having COL. While even the outer layers can affect k₂₂ in late-type stars, these layers, supposed to be most influenced by the mass loss or accretion, contribute little to k₂₂ of the early-type stars. The components of ET-systems therefore should be more similar to the point-like masses. Moreover, radiative outer layers can react only on the Kelvin-Helmholtz time scale ( $\approx10^{5}$ years). Fluctuations in the outer layer of a star, such as those supposed for the late-type loser in RW Tau by Simon (1997c), are then unlikely to produce the observed variations of the periods in ET-systems. These arguments bring another support to the interpretation of the period changes in ET-systems in terms of the mass transfer processes.

An additional mechanism which can play a role in the period changes of ET-systems is a conversion of the orbital angular momentum (OAM) into rotational angular momentum of the gainer (RAM) during the mass exchange, as was treated by Wilson & Stothers (1975). The oblique impact of the stream can spin-up the gainer and increase thus RAM of this star. This value is removed from OAM. This process will therefore tend to decrease the length of the orbital period. We can judge the efficiency of this mechanism from the position of the binary in the r-q diagram. The stream strikes the gainer almost perpendicularly to its photosphere in systems with high $r=R_{\rm g}/a$ and does not spin-up this star significantly. Moreover, the tidal coupling in such close systems is strong and will effectively synchronize the rotation of the gainer. As can be seen in Fig. 20 the degree of the asynchronous rotation in ET-systems of this set generally grows with decreasing r and begins to be appreciable for systems with r smaller than about 0.3. We can conclude that while the contribution of this mechanism is small for close systems with r>0.3 the situation is different in wider binaries (namely AQ Cas, V 356 Sgr) since the impact of the stream is almost tangential (Fig. 17a) and the spinning-up very efficient (Fig. 20). The magnitude of the period changes can be therefore considerably diminished. The efficiency of this conversion is about 80% in case of AQ Cas, it means that the remaining period change inferred from the photometric determination of $\dot m$ (Olson & Bell 1989) can be then completely hidden in the scatter of the data (Fig. 6). The conversion is even larger in the case of V 356 Sgr.

The influence of this conversion is further amplified in the systems which are in an advanced state of evolution and have thus small q. As was demonstrated by Ureche (1976) the ratio of RAM to OAM increases for q significantly different from unity, it means that the role of the rotational momentum of the components becomes appreciable here, namely if the rotation of the gainer is highly asynchronous.

This research has made use of the international database of timings and I thank F. Agerer for providing me with the data. I also thank Dr. Z. Mikulásek for reading the manuscript and for the comments. This study was supported by the project K1-003-601/4 Astrophysics of non-stationary stars of the Academy of Sciences of the Czech Republic.

7 Discussion