3 Sources of the data and analysis of the O-C graphs

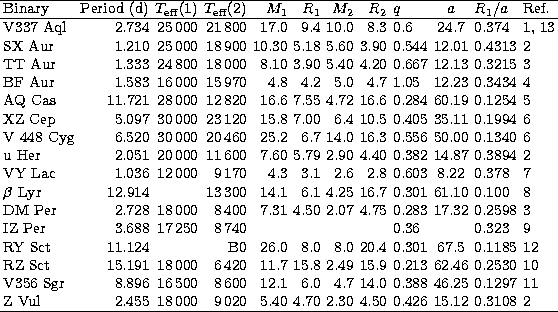
An extensive search for ET-systems was undertaken in the literature. Only systems for which solutions of the light curve giving the semi-detached configuration (or very close to it) and preferably also the spectroscopic observations exist were used for the following analysis. The number of the suitable systems was also inevitably lowered by the requirement of a good coverage by the timings amounting several decades. The parameters of the final ensemble of binaries are summarized in Table 1 where also the sources are cited. The radii of the gainers in $\beta$ Lyr and RY Sct, supposed to be veiled by the accretion disk, were obtained by an interpolation in the table given by Harmanec (1988). These radii were determined for the masses and inferred spectral types given in the cited papers.

  

Table 1: The parameters of binaries with early-type components used for this analysis. The effective temperatures of the primary (gainer) and secondary (loser) component are given in the columns $T_{\rm eff}(1)$ and $T_{\rm eff}(2)$, respectively. The mass and radius of the gainer are denoted as M₁, R₁ while those of the loser are marked by M₂ and R₂. These values are in solar units. The mass ratio q is calculated as M₂/M₁. The orbital separation a (in solar radii) is given along with the fractional radius of the primary R₁/a

References: 1. Giuricin & Mardirossian (1981a); 2. Hilditch & Bell (1987); 3. Figueiredo et al. (1994); 4. Kallrath & Kamper (1992); 5. Olson (1994); 6. Harries et al. (1997); 7. Semeniuk & Kaluzny (1984); 8. Harmanec (1990); 9. Wolf & West (1993); 10. Olson & Ezel (1994); 11. Popper (1980); 12. Skulskij (1992); 13. Alduseva (1977).

The international database of timings of minima of the eclipsing binaries founded by Mr. Lichtenknecker and now directed by F. Agerer was the main source of timings used for this analysis (Agerer 1995, 1996). The O-C values were calculated for the timings of each binary according to the ephemerides found in the literature in the first step (usually SAC No. 67, Danielkiewicz- Krosniak and Kurpinska- Winiarska 1996, hereafter SAC96). Since the timings were obtained by various methods the widely accepted weights (photoel. = 10, photographic = 3, visual = 1) were attributed to the single timings. The O-C graphs were submitted to a visual inspection. In some cases when a large amount of visual minima was available these timings were grouped into bins of several observations and averaged. Such means were given higher weights. Several largely deviating minima were rejected from the sets.

Errors of the photoel. timings are usually smaller than the symbols used and therefore do not represent serious problem. Unfortunately, the accuracies of the visual and photographic timings, generally having larger scatter, are not available in many cases. One possible way how to assess them is a visual inspection of the O-C diagrams. As can be seen from the attached figures most these data are in a good agreement with the photoelectric ones. Accuracy of the visual and photographic timings was further evaluated by linear fits of these data inside the well covered segments of the O-C curves where the period P could be approximated as roughly constant. The 1$\sigma$errors of these timings were then determined from the residuals of the fit using the least squares method.

In general, the course of the O-C changes is often complicated and it is not possible to give any unique method for their analysis. An overview and discussion of the existing methods and general considerations of analysis of an O-C diagram can be found in Simon (1997c). The visibility of the period change becomes considerably suppressed with the growing slope of the O-C curve on the plot. The period lengths were therefore calculated to give the slope close to zero in a large part of the curve. The photoelectric observations which well define the O-C curve are usually found in the second half of the interval covered by the timings in the systems analysed here. In this case it often appears advantageous to keep the slope of these photoelectric data close to zero since the eventual period change (namely if it is inferred from the old timings obtained by other methods) can be more easily resolved and evaluated.

We admit that indication of the period change in a given binary is dependent on the chosen criteria to some extent. We will consider the period change in a given binary as present if it can be resolved by the visual inspection of the O-C diagram which is constructed according to the principles listed above. Its course must be defined by multiple observations. Polynomial fits to the O-C values (e.g. Kalimeris et al. 1994) appear to be a plausible method of analysis of the period change in our case. We note in advance that such fits to the O-C values of the respective systems analysed here have shown that even the most variable periods could be plausibly matched by the second order polynomials. Comparison of the sum of the squares of the residuals of the linear ($C_{\rm LIN}$) and parabolic ($C_{\rm PAR}$) fits of the data can then serve as another clue in assessment of the period change. We will therefore introduce the ratio $S = C_{\rm LIN}/C_{\rm PAR}$; the larger S, the better defined variation. The results, discussed for the respective systems below, have shown that monotonic change of the O-C values can be usually well recognized for S =1.2; this figure may be accepted as a typical limiting value above which the period can be regarded as variable. Discussions of the data and variability of the periods of the respective systems are given below.

The O-C values in the diagrams plotted here are expressed in days as is usual. Nevertheless, it should be noted that the range of the period lengths in the respective systems analysed here is high and amounts about one to ten. The longer periods generally imply longer duration of the eclipse what leads to a larger scatter of the O-C values. This scatter is more pronounced especially for the timings obtained by other methods than photoelectric. If the variations of the O-C values are expressed as a fraction of period P instead of days, eventually if the O-C values are scaled down according to the respective period lengths of the systems then it can be shown that these values for the different systems usually display comparable scatter.