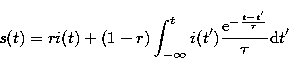
If the number of readouts
per sky position or spectral CVF position is large enough to show a
significant fraction of the transient curve, it is possible to fit
pixel per pixel the temporal response using a specific function to
derive as well as possible a "stabilized'' value. Several methods
have been developed based on the fit, and we found them less reliable
when considering the flux, than the inversion method described in the
following (see Sect. 6.6). Furthermore, for most of
the observations, only the first part of the transient curve is
observed because of the low IR emission of the sources observed with
ISOCAM (especially using the CVF). The LW detector will thus never
reach any stabilized value during the observation. The principle of
the method presented here and developed by Abergel et al. (1996)
consists in inverting a simple model of the CAM-LW response in order
to recover frame by frame the successive stabilized values.
The idea is to describe the response s(t) of one given pixel as a
function of the input flux i(t) (in units of ADUg-1s-1,
i.e. proportional to the incoming flux density, dark subtracted but
not flat-field or distortion corrected):
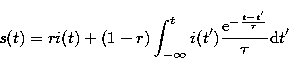 |
(19) |
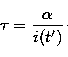 |
(20) |
From preliminary fitting of the model with the transient responses
recorded during a dedicated orbit (revolution 16, during the
Performance Verification phase, where cycles of filter sequences were
performed), the values of r and ![]() have been adjusted to r =
0.6 and
have been adjusted to r =
0.6 and ![]() = 1200 s(ADUg-1s-1)-1 (uncertainties
are around 10%). The low
signal to noise ratio has not allowed the detection of any significant
variations of these values between pixels, though these are likely to
occur.
= 1200 s(ADUg-1s-1)-1 (uncertainties
are around 10%). The low
signal to noise ratio has not allowed the detection of any significant
variations of these values between pixels, though these are likely to
occur.
The camera is not read continuously but rather we obtain
a discrete series of readouts for all tj. Thus we can rewrite
Eq. (19) in this way:
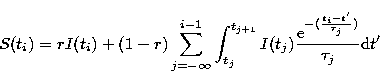 |
(21) |
During an integration, it is assumed (1) that one given pixel sees the
same point in the sky and (2) that the configuration of ISOCAM is
constant. The effects due to the jitter during the integration are
neglected. Thus I(t) is constant between tj and tj+1 and
the integral of Eq. (21) can be computed for all
the terms in the summation. We have:
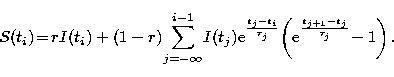 |
(22) |
The transient correction consists of computing the successive values
of I(tj) from the successive CAM readouts S(tj). It is
important to note that r and ![]() are fixed parameters of the
model: this method does not use any fitting and can be applied
whatever the state of the camera and the flux step are. The idea is
to invert the Eq. (22), which can easily be done with
the two following assumptions:
are fixed parameters of the
model: this method does not use any fitting and can be applied
whatever the state of the camera and the flux step are. The idea is
to invert the Eq. (22), which can easily be done with
the two following assumptions:
If our observation is made of N readouts
obtained at time t0, t1, ..., tN-1, we can rewrite
Eq. (22) for each
pixel in a matrix of the form: ![]() . S is the vector of N readouts, i.e. the data, I is the
vector of N intensities, i.e the data corrected for transients, [M]
is an
. S is the vector of N readouts, i.e. the data, I is the
vector of N intensities, i.e the data corrected for transients, [M]
is an ![]() transfer matrix whose elements Mi,j are such
that:
transfer matrix whose elements Mi,j are such
that:
and C is is a vector of constants due to assumption (1) such
that for all i, ![]() .
.
Thus for all instants ti one has ![]() .
.
The transient correction consists in computing ![]() , which is always possible since the
determinant of the matrix [M] is never equal to zero (all elements
above the main diagonal are equal to 0). If the correction is
perfect, the vector I represents the successive values measured by a
detector with no memory effect.
, which is always possible since the
determinant of the matrix [M] is never equal to zero (all elements
above the main diagonal are equal to 0). If the correction is
perfect, the vector I represents the successive values measured by a
detector with no memory effect.
This method of correction allows us to derive in a systematic way, a first
order estimate of the sky brightness observed with ISOCAM-LW, without
any parameter adjustment. However, one should say right away that the
resulting correction is not perfect, since it is limited in
precision by the precision of the model of the CAM-LW response we use
which is obviously oversimplified. In particular, for large flux steps,
the memory effect is predicted to be damped too fast. The model of the
response we use is approximate. We have already pointed out that
upward and downward transients resulting from large flux steps
(typically 80ADUg-1s-1) are not symmetrical and depart
from a simple exponential behavior, while the model is symmetrical and
exponential. The photometric accuracy of the LW channel of ISOCAM is
actually of ![]() after applying the transient correction algorithm
we have presented in this paper. It is not better for strong sources
than for faint sources, because of the over-simplification of the
model of the response we use. We are currently working on algorithms
to correct ISOCAM-LW data from transient effects taking into account
the charge coupling, which introduces most of the features in the
response curves not taken into account at the present time.
after applying the transient correction algorithm
we have presented in this paper. It is not better for strong sources
than for faint sources, because of the over-simplification of the
model of the response we use. We are currently working on algorithms
to correct ISOCAM-LW data from transient effects taking into account
the charge coupling, which introduces most of the features in the
response curves not taken into account at the present time.
Figure 6 shows an example of transient correction in the two general cases of observation of diffuse emission: when CAM first points at a region of zodiacal background, then to a diffuse emission region, then back. The correction appears to be good. Various levels of flux that were blurred due to transients in the original data, because CAM did not spend enough time on each position to become stabilized, become obvious on the corrected data, even for small flux steps. As mentioned earlier, the representation that has been adopted to describe the response of ISOCAM-LW is not fully adequate. In particular it is unable to correctly predict the behavior of transients due to strong flux steps. This is illustrated in Fig. 7 where we show data coming from two pixels that see the brightest region of an observation of Centaurus A in the LW3 filter and with the 3'' pixel field-of-view lens. In the upper panel a strong step occurs and as a result, the corrected data (thick line) show an overshoot for the upward transient and an undershoot for the downward transient. This effect is much reduced in the lower panel where the maximum flux steps are 1/2 those in the upper panel.
We therefore selected a number of observations that satisfy the
following constraint: the source is extended but does not fill the
array, and it is observed using a long raster. Thus it is easy to find
pixels that will spend enough time on the background so that they are
nearly stabilized, see part of the source for one raster
position, and then observe the background again. Therefore the
incoming flux history is very simple and can be written as:
![]() , where
, where
![]() is the background flux, and
is the background flux, and ![]() the source
flux. Given the selection criteria we have applied,
the source
flux. Given the selection criteria we have applied, ![]() can
safely be assumed to be the flux measured on the pixel prior to the
raster position that sees the source. The instant at which the fluxes
change are also easily derived from the data given the existence of
the fast component in the pixel's response.
can
safely be assumed to be the flux measured on the pixel prior to the
raster position that sees the source. The instant at which the fluxes
change are also easily derived from the data given the existence of
the fast component in the pixel's response.
We have then tried to fit the response model (19) to the
observed signal, letting the model parameters r and ![]() vary. We
thus have three parameters to derive from the fit:
vary. We
thus have three parameters to derive from the fit: ![]() , r and
, r and
![]() . The results of this study have been presented elsewhere
(Sauvage 1997) but we summarize them here.
. The results of this study have been presented elsewhere
(Sauvage 1997) but we summarize them here.
Point (3) is in total contradiction with the transient behavior
deduced from ground-based controlled experiment; in these we observed
that the lower the flux, the longer the detector took to stabilize. It
therefore casts serious doubts on the values of ![]() found in the
fit.
found in the
fit.
The main conclusion of this study is thus that the quality of the fit cannot guarantee that the result is photometrically correct. We thus caution observers against fitting methods for transient correction as they offer little control on the validity of the resulting photometry.
In the present case, we interpret the discrepancy between point (3)
and our experimental knowledge of the detector as beeing due to an
oversimplification of the response function (Eq. 19):
it does not account for a slow part in the transient behavior and
fails to reproduce transients observed on strong sources (see
Fig. 7). Nevertheless, the values of r and ![]() are such that (1) memory effects are quite significantly reduced, and
(2) residual photometric errors are limited and can be quantified to
are such that (1) memory effects are quite significantly reduced, and
(2) residual photometric errors are limited and can be quantified to
![]() 10%.
10%.
Copyright The European Southern Observatory (ESO)