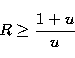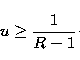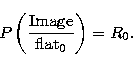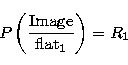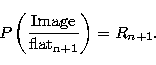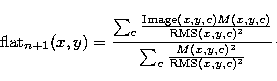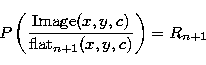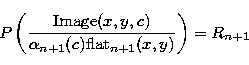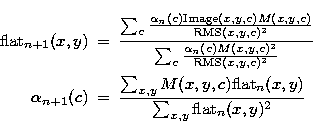Up: ISOCAM data processing
Subsections
In order to improve the estimated flat field, we can use the fact that
a sky point is seen by several pixels of the detector. We consider:
- R = number of raster positions
- a = 322 number of pixels of the detector
- u = detector overlap (u=0 for no pixel overlap, and u=1
for pixel overlap)
- N = total number of pixels in the final image.
The number of unknown variables X should be less than the number D
of data. We have X = N + a (final image + flat), and the number of
data is equal to 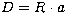 . The final image size depends on both
the overlap factor and the number of raster positions:
. The final image size depends on both
the overlap factor and the number of raster positions:
| <I>NI> = <I>aI> + <I>aI>(<I>RI>-1)(1-<I>uI>) = <I>aI>(<I>RI> - <I>uRI> + <I>uI>) |
|
|
(7) |
then 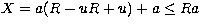 implies that
implies that
| 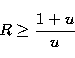 |
(8) |
or
| 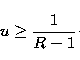 |
(9) |
These relationships give only an idea of the limits, because they do not
take into account effects such as transients, field of view
distortion, noise, etc. As a rule of thumb, one can consider that in
practice an increased number of raster positions and pixel overlap
will result in a better determination of the system.
We represent the reduced data (without flat field correction) by
Image(x,y,c), where x,y is the position on the detector, and c
the raster position number or configuration number. From Image and
from an initial flat flat0, we can build a raster image R0(k,l).
| 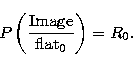 |
(10) |
From the sky image R0, we can simulate our data by applying what we call an
inverse projection. We obtain the set M(x,y,c)
| <I>MI>(<I>xI>,<I>yI>,<I>cI>) = <I>P-1I>(<I>R0I>(<I>kI>,<I>lI>)) |
|
|
(11) |
M can be considered a model of what we should get on the detector
if the true sky image is R0. This model can be used to obtain
an estimation (flat1) of the flat. This new flat will then lead to a
new raster image, R1
| 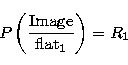 |
(12) |
or in a more general way, we have the iterative flat field correction
| 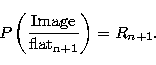 |
(13) |
The problem is now to find flatn+1 knowing Image and our sky model
M. The least square solution gives
| 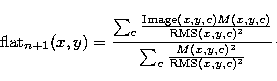 |
(14) |
Furthermore, we can assume that the flat is varying with the time. Then the
Eq. (13) becomes
| 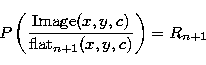 |
(15) |
and if we assume a linear variation constant over the whole image, we have
| 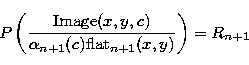 |
(16) |
we now have one more unknown. At each iteration, we compute
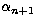 , and flatn+1 by
, and flatn+1 by
| 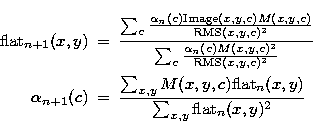 |
(17) |
| (18) |
at each iteration, the flat and 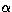 are normalized
Simulations showed that the flat error can be divided by a factor of
two (in our simulations, we derived a flat with a 5% accuracy, starting
with a flat where the error was 10%).
The parameter
are normalized
Simulations showed that the flat error can be divided by a factor of
two (in our simulations, we derived a flat with a 5% accuracy, starting
with a flat where the error was 10%).
The parameter 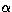 is particularly useful for the first
configuration when the detector is not stabilized at all.
is particularly useful for the first
configuration when the detector is not stabilized at all.


Up: ISOCAM data processing
Copyright The European Southern Observatory (ESO)
![]() . The final image size depends on both
the overlap factor and the number of raster positions:
. The final image size depends on both
the overlap factor and the number of raster positions: