The number of photons emitted in a spectral line (![]() ) for an
optically thin coronal plasma
is given by:
) for an
optically thin coronal plasma
is given by:
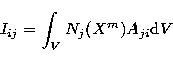 |
(1) |
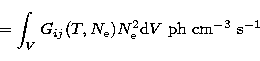
The function ![]() may be expressed as
may be expressed as
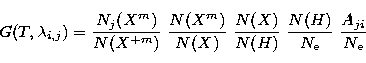 |
(2) |
and
The element abundance and the ionisation balance population of each ion are known from the literature (Allen 1973; Feldman et al. 1992; Meyer 1985; Grevesse & Anders 1992; Waljeski et al. 1994 for the element abundances, Shull & Van Steenberg 1982; Arnaud & Rothenflug 1985; Arnaud & Raymond 1992; Landini & Monsignori Fossi 1991 for the ionisation equilibrium), while the level population must be calculated solving the statistical equilibrium equation including all the important processes involved in level excitation and de-excitation. In low density plasmas the most important populating and de-populating processes are spontaneous radiative decay and excitation and de-excitation from electron-ion collisions, since they are generally faster than ionisations and recombinations. In hot plasmas proton collision rates can also be important in determining the level population.
The statistical equilibrium equations take the form
| |
(3) |
![]()
The collisional excitation rate for a Maxwellian electron velocity distribution can be expressed as
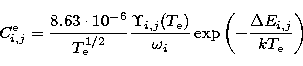 |
(4) |
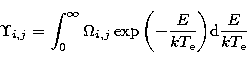 |
(5) |
For solving the statistical equilibrium in Eq. (3) it is necessary to have a large dataset which includes an atomic model with experimental energy levels and radiative and collisional transition probabilities for all the possible transitions within the levels of the adopted atomic model. For this reason in the recent past several extensive databases of theoretical data have been developed, such as ADAS (Summers et al. 1996) and CHIANTI (Dere et al. 1997). Both these databases allow the complete solution of the system of equation described above for the most important ions, though both of them neglect, at the moment, the proton collision rates.
The aim of the present update of the Arcetri spectral code is to renew the entire set of theoretical data which composed the old version of the Code, as described in Landini & Monsignori Fossi (1990) and Monsignori Fossi & Landini (1996), which included the most important emission lines in the range 1 - 2000 Å. For the evaluation of their emission the assumption was made that the population of the upper level of the transition j occurs mainly by collisional excitation from the ground level g and the radiative spontaneous decay dominates any other depopulation process. The old version also included a full set of atomic data which allowed the solution of the statistical equilibrium equation for the ions of the Beryllium, Carbon and Nitrogen isoelectronic sequences and for the Iron Ions from Fe IX to Fe XXIV.
In the present update we have included the whole CHIANTI dataset in the Arcetri spectral code, and we have also added some original data:
The program evaluates level population and contribution functions
for temperature ranging between 104 and 108 K and any electron density, usually
assumed between 106 and 1015 ![]() .Also continuum emission from free-free, free-bound and two-photon
processes is evaluated.
.Also continuum emission from free-free, free-bound and two-photon
processes is evaluated.
An example of the continuum emission is shown in Fig. 1.
The selection of the data for the minor elements has been carried on using the excellent reviews given in the CHIANTI paper (Dere et al. 1997), Pradhan & Gallagher (1992), Itikawa et al. (1984) and Itikawa (1991) and (1996). The paucity of theoretical calculations in the literature (especially for collisional data) has often severely restricted the range of possible choices. The minor elements dataset have been developed mainly adopting theoretical results calculated using the University College of London distorted wave program (Eissner & Seaton 1972) and the close coupling (CC) R-Matrix package (Burke et al. 1971; Berrington et al. 1978) developed at Queens University of Belfast. Like the CHIANTI data, the minor elements dataset allows to evaluate the statistical equilibrium level population. Nevertheless no collision data are available for the Magnesium-like, Oxygen-like, and nitrogen-like minor elements, so it has been necessary to interpolate the effective collision strengths and the radiative data from the isoelectronic ions which were available in the CHIANTI database. The quality of the interpolation depends heavily on the accuracy of the existing data, and in some cases there are severe limitations to the reliability of the interpolated results.
Copyright The European Southern Observatory (ESO)