3 Application to some infrared neutral He lines

3.1 Atomic data

We give in the following the wavelengths of the studied Helium lines, the corresponding transitions, and the perturbing levels i' and f'.

The energy levels have been taken from Martin (1973). For the g-levels which are missing, we have calculated the energies by using an asymptotic expression of the quantum defect and the polarisation potential (Deutsch 1969).

Calculations of oscillator strengths which enter the expressions of the semi-classical cross-sections and the A parameters have been obtained with the Bates & Damgaard approximation. Owing to the high levels involved, this approximation is sufficient. Moreover these transitions and the corresponding high levels are not included in the recent and sophisticated data of TOPbase (Cunto et al. 1993). Thus for the calculations of the oscillator strengths we have updated a code given by Dimitrijevic who used the tables by Oertel & Shomo (1968) and the Van Regemorter et al. (1979) formula adapted for high levels. For the transitions between the very high levels nf-n'g (n, n' > 7), we have used the Coulomb approximation, the corresponding quantum defects being negligible.

3.2 Results and discussion

3.2.1 Calculations

The calculations have been made for a grid of temperatures (10⁴ to 10⁵ K) and electronic densities (10¹⁰ to 10¹³ cm^-3) typical of stellar atmospheres conditions of hot early-type stars. The results are displayed in Tables 1-12 for the six studied helium lines. We give the calculated impact widths W and the shifts d for collisions with electrons, protons, He⁺ and He⁺⁺ ions and the quasistatic parameter A. We give also the various validity criterions useful for the following discussion.

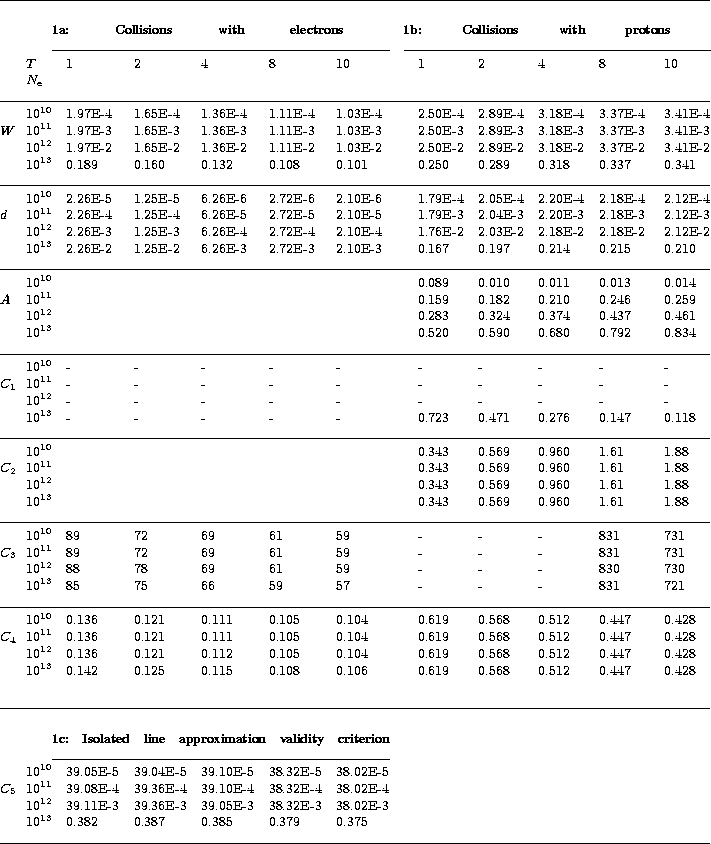
C₁ is the impact validity criterion.

$C_{2}={W_{\rm inel}\over W_{\rm el}}$ gives the ratio of the contribution of inelastic collisions versus elastic ones for the width.

C₃ is the criterion for the "one state'' approximation validity criterion.

C₄ is the ratio of the contribution of strong collisions to the total impact width and thus gives a validity criterion for the perturbation theory approximation.

C₅ is the criterion for the isolated line approximation, defined by (Dimitrijevic & Sahal Bréchot 1984; Baranger 1958b).

$C_{5}={W}/\big (\Delta E_{ii'}\big )_{\rm min}$,

where W is the total width,

$W=W_{\rm e}+0.9W_{\rm H^{+}}+0.1W_{\rm He^{+}}$,

$W_{\rm e}$ is the width due to electron collisions, $W_{\rm H^{+}}$ that due proton collisions and $W_{\rm He^{+}}$that due to collisions with He⁺. We neglect collisions with He⁺⁺ in this criterion and we assume that protons and He⁺ ions are in proportion of 90% and 10% respectively.

$\big (\Delta E_{ii'}\big )_{\rm min}$ is the energy distance between the upper level and the nearest perturbing level.

3.2.2 Validity criterions of impact and quasistatic approximations

Impact approximation is always valid for electron collisions, because the corresponding values of C₁ are very small compared to unity for all temperatures and densities of interest. In fact it can break down for collisions with ions at low temperatures and high densities (we consider that for C₁>0.5 the impact approximation fails in the line center). It breaks down especially in the wings where the quasistatic approximation condition becomes $\tau \Delta \omega \gg 1$ where $\Delta \omega$ is the detuning. In astrophysics the detuning of interest is very much larger than the collisional half-width because the wings are sensitive to collisions whereas the line center is dominated by the Doppler broadening. Consequently the collisional wings, due to interactions with ions must often be treated within the quasistatic approximation. For obtaining this quasistatic contribution, we have to determine the predominant interaction of interest. For that we argue by looking at the impact regime and we extrapolate to the quasistatic one: if inelastic collisions are dominant ($C_{2}\gg 1$ of Tables 1-12) for the broadening of the studied lines in the impact approximation, we will consider that the same dipolar interaction can be used in the quasistatic regime: then the so-called linear Stark effect is to be used. On the contrary, if elastic collisions are dominant ($C_{2}\ll 1$) for the broadening of the studied lines, we look at the relative importance of the quadrupolar and polarisation ("quadratic interaction'') potential. We have verified that the quadrupolar interaction is always negligible for the all lines studied in this paper. This is due to the fact that the upper levels of the lines studied are highly excited. Thus the broadening by elastic collisions is entirely due to the polarization potential. This corresponds to the quadratic Stark effect in the quasistatic regime. In that case the A parameter Griem (1974) is relevant for obtaining the contribution of the ions to the total width.

Our calculations show that for all studied lines, when the impact approximation is not valid (C₁>1), the elastic collisions are generally dominant (C₂<1). Consequently in most cases, the quasistatic effect is quadratic. The opposite case (C₂>1) only occurs for high densities and for low temperatures, for the two following lines: 8651 Å for collisions with He⁺⁺ and 10028 Å for collisions with protons, He⁺ and He⁺⁺. For these two cases of minor importance, the quasistatic treatment involves the dipolar interaction and is not treated in the present paper.

3.2.3 Isolated lines and overlapping lines cases

According to Dimitrijevic & Sahal-Bréchot (1984), if C₅< 1, energy levels broadened by collisions do not overlap. Then the line is isolated. If C₅> 1 we have in principle to treat the problem of overlapping lines. We show that, for all the studied lines of the present paper, the problem does not appear. The isolated line criterion is always satisfied for the lines: 10138 Å, 8779 Å, 8651 Å, and 8584 Å. In fact, the criterion is not satisfied for the line 10028 Å at densities equal or higher than 10¹² cm^-3. For the 8736 Å line, the criterion is not satisfied for densities equal or higher than 10¹¹ cm^-3. However, if we look at the ratio of the contribution of the upper level to that of lower level to the impact width (the C₃ criterion), we conclude that the "one state'' approximation is always valid, because the lower level contribution is always negligible ($C_{3}\gg 1$). Therefore the off-diagonal elements (Baranger 1958b) which enter the expression of the line profiles of overlapping lines in the "two state case'' can be neglected. Consequently it is possible to continue to use the isolated line approximation in the "one state case'' for the present studied lines which should be a priori not isolated.

In addition, we have checked the validity condition of the perturbation theory. The validity criterion is given by C₄, which represents the relative contribution of strong collisions to the total impact width. It is well satisfied (C₄ does not exceed a few 20%) for collisions with electrons. For collisions with ions, the strong collision contribution is more important (C₄ is of the order of 65%) and the perturbation approximation is not so good.

Finally, it can be noticed that the ionic shifts of 8651 Å and 8736 Å lines present some deviations from linearity at 10¹³ cm^-3 due to the Debye cut-off.

3.2.4 Summary of the discussion

Considering the validity conditions discussed above, our data can then be used for astrophysical purposes as follows:

1. If the impact approximation criterion ($C_{1}\ll 1$) is satisfied, the resulting profiles are lorentzian, and the total widths and shifts are given by:

$W=W_{\rm e}+W_{\rm H^{+}}+W_{\rm He^{+}}+W_{\rm He^{++}}$,

$d=d_{\rm e}+d_{\rm H^{+}}+d_{\rm He^{+}}+d_{\rm He^{++}}$.

2. If the impact approximation criterion is satisfied for electronic collisions and not satisfied for the collisions with ions, then the quasistatic approximation can be used:

2a. If C₂> 1, the quasistatic interaction is dipolar. This case is not treated in this paper.

2b. If the quasistatic interaction is quadratic (C₂< 1), which is the predominant case, the resulting widths and shifts are given by:

$W=W_{\rm e}+W_{\rm iq}$,

$d=d_{\rm e}+d_{\rm iq}$.

However, it must be noticed that an intermediate region between the impact and quasistatic approximations is expected for collisions with ions, for which neither of the two limiting approximations is valid. For such conditions the static model employed can only give an estimate for the line shape.

  

Table 1: Present calculations for the transition 7 ¹D-3 ¹P of Helium ($\lambda = 10138$ Å) - T: electronic temperature in 10⁴ K - $N_{\rm e}$: electronic density in cm^-3. - W and d: impact half-width and shift (positive shifts are towards the red) in Å - A: quasistatic quadratic broadening parameter - C₁: impact approximation validity criterion (not mentioned if C₁< 0.1) - C₂: ratio of inelastic collisions contribution to the elastic collisions one to the impact width - C₃: one state approximation validity criterion (ratio of the contribution of the upper level to that the lower level to the impact width, not mentioned if C₃>1000) - C₄: perturbation theory validity criterion (contribution of strong collisions to the impact width) - C₅: isolated line approximation validity criterion

  

Table 2: Same as Table 1

  

Table 3: Same as Table 1 but for transition 9 ³D-3 ³P of Helium ($\lambda = 8779$ Å)

  

Table 4: Same as Table 3

  

Table 5: Same as Table 1 but for transition: 13 ³F-3 ³D of Helium ($\lambda = 8651$ Å)

  

Table 6: Same as Table 5

  

Table 7: Same as Table 1 but for transition 10 ³D-3 ³P of Helium ($\lambda = 8584$ Å)

  

Table 8: Same as Table 7

  

Table 9: Same as Table 1 but for transition 12 ³F-3 ³D of Helium ($\lambda = 8736$ Å)

  

Table 10: Same as Table 9

  

Table 11: Same as Table 1 but for transition 7 ³F-3 ³D of Helium ($\lambda = 10028$ Å)

  

Table 12: Same as Table 11