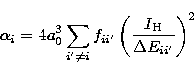Up: Stark profiles of infrared
Using the Sahal-Bréchot code based on the Sahal-Bréchot
theory (Sahal-Bréchot 1969, cf. also Baranger 1958a-c for the basic
theory) and constanly
updated (cf. for example Ben Nessib et al. 1996), which assumes: the
impact approximation, the semi-classical approximation (the radiator is
treated quantically and the perturbers follow classical paths,
which are straight lines in the
case of neutral radiating atoms) and the perturbation theory, we have calculated
the full half width 2W and the shift d of the line emitted between the
initial level i and the final level f which are given by the
following formulae (Sahal-Bréchot 1969):
|  |
(1) |
|  |
(2) |
i' and f' are the perturbing levels, N and v are respectively the density and the velocity of
perturbers, f(v) is the Maxwellian distribution of velocities.
The inelastic cross sections  (respectively
(respectively  )can be expressed by an integration over the
impact parameter
)can be expressed by an integration over the
impact parameter  of the transition probability Pii' as
of the transition probability Pii' as
|  |
(3) |
The elastic collision contribution to the width is given by:
|  |
(4) |
| 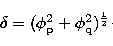 |
(5) |
The phase shifts  and
and  are due respectively to
the polarisation and the quadrupole potential (Sahal-Bréchot 1969).
are due respectively to
the polarisation and the quadrupole potential (Sahal-Bréchot 1969).
The cut-offs R1, R2, R3, the Debye cut-off  and the symmetrization procedures are described by Sahal-Bréchot (1969)
and further papers and will not be rediscussed therein.
and the symmetrization procedures are described by Sahal-Bréchot (1969)
and further papers and will not be rediscussed therein.
As already discussed by Baranger (1958a-c, 1962) and Sahal-Bréchot
(1969), the impact approximation is valid when the average effect of
collisions is weak, in other words when strong collisions are separated in
time, or equivalently,
when the duration of a collision is very small compared to the separation
time between strong collisions.
The validity criterion for the impact approximation is given by:
|  |
(6) |
where  is a typical collision duration and
is a typical collision duration and  is the
strong collision contribution to the
collisional half-width. It can also be written as (Ben Nessib et al. 1996):
is the
strong collision contribution to the
collisional half-width. It can also be written as (Ben Nessib et al. 1996):
|  |
(7) |
where  is a typical impact parameter for strong collisions.
is a typical impact parameter for strong collisions.
The resulting profiles are Lorentzian.
This condition is well verified by electronic collisions for a
large range of densities.
For ionic collisions the impact approximation fails,
especially for high densities. Then we can apply the quasistatic
approximation.
If the quadratic interaction potential is dominant, the quasistatic total
width and shift are given by (Griem 1974):
| ![\begin{displaymath}
W_{\rm iq}=1.75 10^{-4}N_{\rm e}^{1\over 4}A\big [1-0.068N_{\rm e}^{1\over
6}T^{-{1\over 2}}\big ]W_{\rm e} \end{displaymath}](/articles/aas/full/1998/20/ds7702/img17.gif) |
(8) |
| ![\begin{displaymath}
{d}_{\rm iq}=10^{-4}N_{\rm e}^{1\over 4}A\big [1-0.068N_{\rm e}^{1\over
6}T^{-{1\over 2}}\big ]W_{\rm e}\end{displaymath}](/articles/aas/full/1998/20/ds7702/img18.gif) |
(9) |
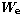 is the impact contribution of electrons to the total width.
is the impact contribution of electrons to the total width.
A is the quasistatic quadratic parameter, defined by Griem (1964),
Traving (1968) and expressed by Ben Nessib et al. (1996) as follows:
| 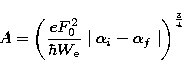 |
(10) |
 is the normal field strength
(Griem 1974).
T is in Kelvin and
is the normal field strength
(Griem 1974).
T is in Kelvin and  in cm-3.
in cm-3.
 is the polarizability of the initial level (resp.
is the polarizability of the initial level (resp.
 is the polarisability of the final level). It is expressed
as:
is the polarisability of the final level). It is expressed
as:
| 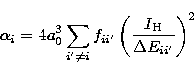 |
(11) |
a0 is the Bohr radius and  is the ionisation energy of
hydrogen.
is the ionisation energy of
hydrogen.


Up: Stark profiles of infrared
Copyright The European Southern Observatory (ESO)



![]() (respectively
(respectively ![]() )can be expressed by an integration over the
impact parameter
)can be expressed by an integration over the
impact parameter ![]() of the transition probability Pii' as
of the transition probability Pii' as


![]() and the symmetrization procedures are described by Sahal-Bréchot (1969)
and further papers and will not be rediscussed therein.
and the symmetrization procedures are described by Sahal-Bréchot (1969)
and further papers and will not be rediscussed therein.
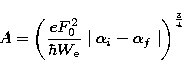
![]() is the polarizability of the initial level (resp.
is the polarizability of the initial level (resp.
![]() is the polarisability of the final level). It is expressed
as:
is the polarisability of the final level). It is expressed
as: