Up: Physical parameters of the curves
Geneva 7-colour photometric measurements of TZ Eridani were obtained
from Dec. 10, 1983 to Dec. 10, 1996, using the Swiss
70 cm telescope at the European Southern Observatory (ESO), La Silla, Chile.
During this period, 429 measurements of weight 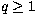 have been obtained
(see Rufener 1988, for the definition of the weight q). These data are
listed in Table 1, including the 36 additional photometric measurements
obtained in Nov.-Dec. 1996 (see Sect. 2).
have been obtained
(see Rufener 1988, for the definition of the weight q). These data are
listed in Table 1, including the 36 additional photometric measurements
obtained in Nov.-Dec. 1996 (see Sect. 2).
The magnitudes in each of the seven filters are obtained from the visual
magnitude V and the six colour indices in the following manner:
|
i = V - [V - B] + [i - B]
|
(4) |
with i representing one of the seven filters U, B, V, B1,
B2, V1, G. Remember that the Geneva [U - B] and [B - V]
indices are not normalized to zero for an A0V star as it is the case for the
Johnson UBV indices.
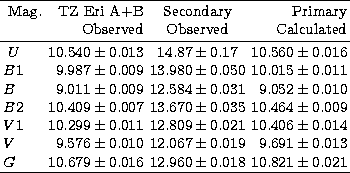
It is possible to calculate the magnitude of the primary (mass gainer) by subtracting
the flux of the secondary (mass loser), at the bottom of the primary eclipse, from
the flux of the both components measured together (outside the eclipses).
This calculation has been made for each of the seven Geneva
magnitudes. In order to minimize the effects of a possible long-term variability
(see the end of this section), only the data obtained in December 1983 and
January 1984 have been used. The results are given in Table 2.
It is interesting to compare
the observed uncertainties with the mean precision of the measurements
made in Geneva photometry. Rufener (1988, Fig. 2) has shown the
shape of the mean relation 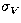 vs. V obtained for the
non-variable stars, in particular the progressive increase of
vs. V obtained for the
non-variable stars, in particular the progressive increase of 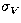 with increasing V, for stars fainter than
with increasing V, for stars fainter than 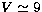 . The same relation
can be applied to the seven Geneva magnitudes. Figure 2 of this
paper shows a new calculation of this relation, based on the up to date
version of our photometric database. On the same figure are plotted the
observed values for TZ Eri given in Table 2. A correction has been
applied to the uncertainties of the magnitudes for the secondary, because
the measurements obtained during the totality of the primary eclipse had
shorter integration time than the other ones (4 minutes instead of 12
minutes). The conclusion is that the uncertainties on the measurements of
TZ Eri are in agreement with the expected precision. Thus, the components do
not exhibit a short-term variability, i.e on a time-scale shorter than about
20 orbital periods.
. The same relation
can be applied to the seven Geneva magnitudes. Figure 2 of this
paper shows a new calculation of this relation, based on the up to date
version of our photometric database. On the same figure are plotted the
observed values for TZ Eri given in Table 2. A correction has been
applied to the uncertainties of the magnitudes for the secondary, because
the measurements obtained during the totality of the primary eclipse had
shorter integration time than the other ones (4 minutes instead of 12
minutes). The conclusion is that the uncertainties on the measurements of
TZ Eri are in agreement with the expected precision. Thus, the components do
not exhibit a short-term variability, i.e on a time-scale shorter than about
20 orbital periods.
Table 2:
The seven Geneva apparent magnitudes of TZ Eri (measures of December 1983 and
January 1984)
|
|
![\begin{figure}
\includegraphics [width=8.8cm]{fig2.ps}
\end{figure}](/articles/aas/full/1998/18/ds7638/Timg28.gif) |
Figure 2:
Variation of the mean precision 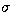 with the magnitude, in the case of Geneva photometric measurements.
The solid thick line refers to the mean value and the solid
thin lines to the 1 s.d. level. Dots and small squares concern respectively the seven
magnitudes of TZ Eri A+B outside eclipses and of the secondary (during the totality of the
primary eclipse). Big squares represent the estimated values of
with the magnitude, in the case of Geneva photometric measurements.
The solid thick line refers to the mean value and the solid
thin lines to the 1 s.d. level. Dots and small squares concern respectively the seven
magnitudes of TZ Eri A+B outside eclipses and of the secondary (during the totality of the
primary eclipse). Big squares represent the estimated values of 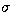 for the secondary
which ought to have resulted from a "normal'' integration time of the measurements,
i.e. 12 minutes (normal) instead of 4 minutes (during the primary eclipse) for the secondary
which ought to have resulted from a "normal'' integration time of the measurements,
i.e. 12 minutes (normal) instead of 4 minutes (during the primary eclipse) |
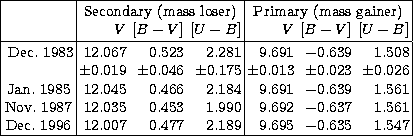
The long-term photometric behaviour of both components has been analysed by
comparing our photometric data obtained at 4 epochs, corresponding to the
intensive monitoring of the eclipses: Dec. 1983 to Jan. 1984, Jan. 1985,
Nov. 1987 and Nov.-Dec. 1996. Table 3 gives the mean values of
V, [B-V] and [U-B] at each of these epochs for the both components. It
appears that:
- 1.
- The secondary exhibited a long-term luminosity increase (0.06 in V)
between Dec. 1983 and Dec. 1996. The colour variations are large,
especially in [U-B], but not significant due to the large standard
deviation.
- 2.
- The primary did not show any long-term variation in magnitude or in colours.
The observed variations of TZ Eri secondary are similar to those studied by
Olson & Etzel (1993) in six cool subgiant secondaries of totally eclipsing
Algol systems. They noted that the fluctuations increase with decreasing
orbital period, or with increasing rotational velocity, suggesting that
rotationally induced magnetic activity could be the origin of these
brightness variations.
In order to minimize the effects of the long-term variation of the secondary
luminosity, only the data obtained before HJD 2447200 (Feb. 1988) have
been used for the eclipse analysis (see Sect. 6).
Table 3:
Long-term behaviour of the components of TZ Eri in V magnitude and Geneva colours
[B-V] and [U-B]. Only the variation of the secondary in V is significant
|
|


Up: Physical parameters of the curves
Copyright The European Southern Observatory (ESO)
![]() vs. V obtained for the
non-variable stars, in particular the progressive increase of
vs. V obtained for the
non-variable stars, in particular the progressive increase of ![]() with increasing V, for stars fainter than
with increasing V, for stars fainter than ![]() . The same relation
can be applied to the seven Geneva magnitudes. Figure 2 of this
paper shows a new calculation of this relation, based on the up to date
version of our photometric database. On the same figure are plotted the
observed values for TZ Eri given in Table 2. A correction has been
applied to the uncertainties of the magnitudes for the secondary, because
the measurements obtained during the totality of the primary eclipse had
shorter integration time than the other ones (4 minutes instead of 12
minutes). The conclusion is that the uncertainties on the measurements of
TZ Eri are in agreement with the expected precision. Thus, the components do
not exhibit a short-term variability, i.e on a time-scale shorter than about
20 orbital periods.
. The same relation
can be applied to the seven Geneva magnitudes. Figure 2 of this
paper shows a new calculation of this relation, based on the up to date
version of our photometric database. On the same figure are plotted the
observed values for TZ Eri given in Table 2. A correction has been
applied to the uncertainties of the magnitudes for the secondary, because
the measurements obtained during the totality of the primary eclipse had
shorter integration time than the other ones (4 minutes instead of 12
minutes). The conclusion is that the uncertainties on the measurements of
TZ Eri are in agreement with the expected precision. Thus, the components do
not exhibit a short-term variability, i.e on a time-scale shorter than about
20 orbital periods.