

Up: Physical parameters of the curves
The orbital period listed in the GCVS (Kholopov 1985) is P = 2.6060653
days. However, we are dealing here with a semi-detached system which, by
definition, has a variable period due to mass transfer. During most
photometric observations done in 1984-1987 by Dr. Zdenek Kviz, the period
remained fairly constant, since it was possible to obtain a well-defined
lightcurve with P=2.6061082 days. This value was obtained using the
reciprocal  test of Renson (1978) - see also Manfroid et al.
(1991) - which had been defined above all for Ap stars (which vary with
small amplitudes) but proved very efficient for a precise determination of
the period of eclipsing binaries. The ephemeris we have adopted is:
test of Renson (1978) - see also Manfroid et al.
(1991) - which had been defined above all for Ap stars (which vary with
small amplitudes) but proved very efficient for a precise determination of
the period of eclipsing binaries. The ephemeris we have adopted is:
| 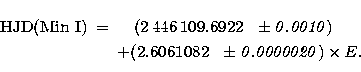 |
(1) |
| |
The orbital period has varied, as shown by the times of minima registered
over decades by amateur astronomers. The O-C values so obtained, and
published in the BSAG Bulletin (e.g. Locher 1997) are shown in
Fig. 1 together with a parabolic fit which gives:
| 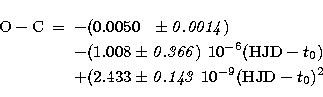 |
(2) |
| |
| |
where t0 = 2446109.6922 . The typical error on the epochs of primary minima
in Fig. 1 is a few minutes (0.002 - 0.005 d). Therefore
the fit only represents a mean trend, upon which are superposed sudden period
changes that cannot be accounted for by measurement errors (see especially the
very steep rise just before JD 2450000).
![\begin{figure}
\includegraphics [width=8.8cm]{fig1.eps}\end{figure}](/articles/aas/full/1998/18/ds7638/Timg19.gif) |
Figure 1:
O-C diagram of TZ Eri from observations made by amateurs and
published in the BSAG Bulletin (two points are defined by Geneva photometry).
A parabolic fit is superposed, showing the
regular increase in the period. Short arrows define the intervals of photometric
measurements; long arrows define the interval of radial-velocity observations |
Although the period changes are interesting by themselves, they are rather
a nuisance in our context, because the radial-velocity measurements, which were
made recently, have to be put in phase with the photometric ones, which are
much older. For this reason we have not used the above formula for O-C,
but we have simply used additional photometric measurements kindly made by Marc
Künzli in November 1996 with the same equipment. He has made 36 new
multicolour measurements, several of which during the primary minimum. Using
the code EBOP16 (Etzel 1989) and the adopted ephemeris, we adjusted the
 parameter (phase correction for the position of the primary
minimum) for these recent data, as well as for the old data alone. The
difference is:
parameter (phase correction for the position of the primary
minimum) for these recent data, as well as for the old data alone. The
difference is:
| 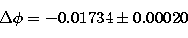 |
(3) |
and represents the phase correction to be
applied to the 1996 data, to fit them into the adopted ephemeris. Although
the  observations have been made one year earlier than the new
photometric ones, we neglect the slight period change that may have
occurred in between, compared to the change that has taken place between the
old photometric measurements and the
observations have been made one year earlier than the new
photometric ones, we neglect the slight period change that may have
occurred in between, compared to the change that has taken place between the
old photometric measurements and the  ones. Therefore, the above
phase shift was applied as such to the
ones. Therefore, the above
phase shift was applied as such to the  data.
data.


Up: Physical parameters of the curves
Copyright The European Southern Observatory (ESO)
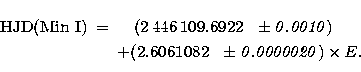
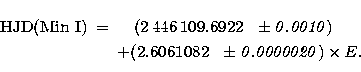
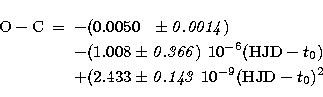
![]() parameter (phase correction for the position of the primary
minimum) for these recent data, as well as for the old data alone. The
difference is:
parameter (phase correction for the position of the primary
minimum) for these recent data, as well as for the old data alone. The
difference is: