With the fitted polynomial coefficients ![]() , we
can write a linear form of the fit as:
, we
can write a linear form of the fit as:
| (A1) |
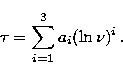
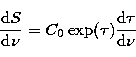 |
(A2) |
![\begin{displaymath}
\frac{{\rm d}^2S}{{\rm d}{\nu}^2} = C_0 \left[\exp(\tau) \fr...
...d}{\nu}^2} +
\exp(2\tau) \frac{{\rm d}\tau}{{\rm d}\nu} \right]\end{displaymath}](/articles/aas/full/1998/17/ds7109/img146.gif) |
(A3) |
![\begin{displaymath}
\frac{{\rm d}\tau}{{\rm d}\nu} = \frac{1}{\nu} [a_1 + 2a_2 \ln\nu +
3a_3(\ln\nu)^2]\end{displaymath}](/articles/aas/full/1998/17/ds7109/img147.gif) |
(A4) |
![\begin{displaymath}
\frac{{\rm d}^2\tau}{{\rm d}{\nu}^2} = -\frac{1}{\nu^2} [3a_3(\ln\nu)^2 +
(2a_2\, -\, 6a_3)\ln\nu + (a_1\, -\, 2a_2)].\end{displaymath}](/articles/aas/full/1998/17/ds7109/img148.gif) |
(A5) |
![\begin{displaymath}
S(\nu) = C_1 \left(\frac{\nu}{\nu_1}\right)^{\alpha_{\rm t}}...
...\nu_1}\right)^{\alpha_{\rm o}-\alpha_{\rm t}}\right]\right\}\,,\end{displaymath}](/articles/aas/full/1998/17/ds7109/img149.gif) |
(A6) |
![\begin{displaymath}
\frac{{\rm d}S}{{\rm d}\nu} = C_1\left[\nu^{\alpha_{\rm t}} ...
...d}\nu} + \alpha_{\rm t}\nu^{(\alpha_{\rm t}-1)} f_{\nu}\right] \end{displaymath}](/articles/aas/full/1998/17/ds7109/img150.gif) |
(A7) |
![\begin{eqnarray}
\frac{{\rm d}^2S}{{\rm d}{\nu}^2} & = & C_1\Bigg[\nu^{\alpha_{\...
...uad\quad\quad\quad
+ (\alpha_{\rm t}-1)\alpha_{\rm t}f_{\nu}\Bigg]\end{eqnarray}](/articles/aas/full/1998/17/ds7109/img151.gif) |
(A8) | |
![\begin{displaymath}
f_{\nu} = 1 - \exp\left[-\left(\frac{\nu}{\nu_1}\right)^{\lambda}\right]\,,\quad
\lambda=\alpha_{\rm o}-\alpha_{\rm t}\end{displaymath}](/articles/aas/full/1998/17/ds7109/img152.gif) |
(A9) |
![\begin{displaymath}
\frac{{\rm d}f_{\nu}}{{\rm d}\nu} =
\frac{\lambda\nu^{\lambd...
...}}
\,\exp\left[-\left(\frac{\nu}{\nu_1}\right)^{\lambda}\right]\end{displaymath}](/articles/aas/full/1998/17/ds7109/img153.gif) |
(A10) |
![\begin{displaymath}
\frac{{\rm d}^2f_{\nu}}{{\rm d}\nu^2}\! =\! \frac{\lambda
\n...
...\!\!\left[-\!\left(\frac{\nu}{\nu_1}\right)^{\lambda}\!\right].\end{displaymath}](/articles/aas/full/1998/17/ds7109/img154.gif) |
(A11) |
Following the same considerations, the logarithmic form for the polynomial fit
and its derivatives are:
 |
(A12) |
 |
(A13) |
 |
(A14) |
| (A15) |
![\begin{displaymath}
\frac{{\rm d}\,f_{\nu}}{{\rm d}(\ln\nu)} = \lambda
\left(\fr...
...da}\,\exp\left[-\left(\frac{\nu}{\nu_1}\right)^{\lambda}\right]\end{displaymath}](/articles/aas/full/1998/17/ds7109/img159.gif) |
(A16) |
![\begin{displaymath}
\frac{{\rm d}^2f}{{\rm d}(\ln\nu)^2} = \lambda^2 \left(\frac...
...,\exp\!\!\left[-\left(\frac{\nu}{\nu_1}\right)^{\lambda}\right]\end{displaymath}](/articles/aas/full/1998/17/ds7109/img160.gif) |
(A17) |
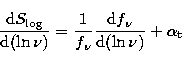 |
(A18) |
![\begin{displaymath}
\frac{{\rm d}^2S_{\rm log}}{{\rm d}(\ln\nu)^2} = \frac{1}{f^...
...
\left(\frac{{\rm d}f_{\nu}}{{\rm d}(\ln\nu)}\right)^2 \right].\end{displaymath}](/articles/aas/full/1998/17/ds7109/img162.gif) |
(A19) |
Copyright The European Southern Observatory (ESO)