The frequency range covered by VLBI observations is very narrow
(roughly, from 1 to 100GHz, with most of the observations done
between 5 and 22GHz). The turnover frequency, ![]() , of the
synchrotron spectrum often lies
outside the range of observing frequencies (see the sketch in
Fig. 6). Because of the limited frequency coverage, a
straightforward application of the synchrotron spectral form to fitting may
be ill-constrained (such as in the case B in Fig. 6). To
provide an estimate of
, of the
synchrotron spectrum often lies
outside the range of observing frequencies (see the sketch in
Fig. 6). Because of the limited frequency coverage, a
straightforward application of the synchrotron spectral form to fitting may
be ill-constrained (such as in the case B in Fig. 6). To
provide an estimate of ![]() in such cases, we first attempt to
achieve the best fit of spectral data by polynomial functions, and then
analyse local curvature of the obtained fit. From the measured curvature,
an estimate (often only an upper limit) of
in such cases, we first attempt to
achieve the best fit of spectral data by polynomial functions, and then
analyse local curvature of the obtained fit. From the measured curvature,
an estimate (often only an upper limit) of ![]() can
be found. Details of spectral fitting are given in Sect. 5.4;
application of the local curvature for determining the turnover frequency
is discussed in Sects. 5.5-5.6.
can
be found. Details of spectral fitting are given in Sect. 5.4;
application of the local curvature for determining the turnover frequency
is discussed in Sects. 5.5-5.6.
For an extensive coverage of synchrotron emission and
its properties, we refer to the works by Ginzburg & Syrovatskii
(1969), Pacholczyk (1970), and Ternov & Mikhailin
(1986). In our calculations, we consider synchrotron
emission from a homogeneous plasma with isotropic pitch angle
distribution and power law energy distribution
![]() ,for electron Lorentz factors
,for electron Lorentz factors ![]() .In this case, it would suffice to describe the emission within the range of
frequencies
.In this case, it would suffice to describe the emission within the range of
frequencies ![]() , where
, where ![]() are the
low-frequency and high-frequency cutoffs given by:
are the
low-frequency and high-frequency cutoffs given by:
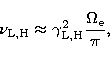 |
(6) |
![\begin{displaymath}
I_\nu \propto \left( \frac{\nu}{\nu_1}
\right)^{\alpha_{\rm ...
...1}{\nu}
\right)^{\alpha_{\rm t}-\alpha_{\rm o}}\right]\right\},\end{displaymath}](/articles/aas/full/1998/17/ds7109/img63.gif) |
(7) |
The main steps of spectral fitting can be summarized as follows:
1) Make an approximate estimate of cutoffs in the spectrum, on the basis of
all available spectral information. A fairly good guess can be
attained by taking the average measured turnover frequency and
optically thin spectral index in the compact source. Based on these values,
calculate the high and low frequencies at which the corresponding flux
density is at an arbitrarily low level (we use ![]() mJy). Add these spectral points to the measured data in each
pixel, in order to ensure a negative curvature of the fitted curves,
as required by the theoretical spectral form (7).
mJy). Add these spectral points to the measured data in each
pixel, in order to ensure a negative curvature of the fitted curves,
as required by the theoretical spectral form (7).
2) Fit the combined pixel spectra by polynomial functions, allowing
for limited variations of the cutoff frequencies, and aiming at
achieving the best fit to the measured data points. From the fits,
determine the basic spectral parameters: the turnover frequency,
turnover flux density, and integrated flux (with integration limited
to the range of observing frequencies). Estimate the errors from Monte
Carlo simulations, using the distribution of the ![]() parameters
of the fits to the simulated datasets.
parameters
of the fits to the simulated datasets.
3. Calculate the local curvature of the fitted spectra within the range of observing frequencies. Compare the derived curvature with the values obtained from analytical or numerical calculations of the synchrotron spectrum. Derive the corrected value of the turnover frequency, by equating the fitted and the theoretical spectral curvatures.
4. Fit the data with the synchrotron spectral form described by (7), and using the corrected value of the turnover frequency.
The above procedure has been applied to spectral data obtained from modelling VLBI images of 3C345 by elliptical Gaussian components, and combining the models at different frequencies (Lobanov & Zensus 1998).
Because the transition between high-frequency (![]() ) and
low-frequency
(
) and
low-frequency
(![]() ) spectral regimes determined by Eq. (7) is
very sharp, the
spectrum is determined by the synchrotron self-absorption at
frequencies
) spectral regimes determined by Eq. (7) is
very sharp, the
spectrum is determined by the synchrotron self-absorption at
frequencies ![]() , and by the electron energy distribution at
, and by the electron energy distribution at
![]() . Estimates of the typical turnover frequency and energy
spectral index in the jet of 3C 345 based on our own calculations and
on the results from Rabaça & Zensus (1994) give
. Estimates of the typical turnover frequency and energy
spectral index in the jet of 3C 345 based on our own calculations and
on the results from Rabaça & Zensus (1994) give
![]() GHz and
GHz and ![]() .Using these values, we estimate the low-frequency,
.Using these values, we estimate the low-frequency, ![]() 1MHz,
and high-frequency,
1MHz,
and high-frequency, ![]() 1000GHz, cutoffs in the spectrum,
and use these values for the spectral fitting.
However, the cutoffs
cannot be well defined, and may change during the
evolution of the jet emission. To account for this effect,
we allow 15% variations
of the cutoff frequencies so as to achieve the best fit to the data.
1000GHz, cutoffs in the spectrum,
and use these values for the spectral fitting.
However, the cutoffs
cannot be well defined, and may change during the
evolution of the jet emission. To account for this effect,
we allow 15% variations
of the cutoff frequencies so as to achieve the best fit to the data.
In order to calculate the spectral parameters of jet emission,
we combine the component fluxes measured at frequencies
![]() , and
add the cutoff information. The resulting spectral dataset
, and
add the cutoff information. The resulting spectral dataset
![]() is
represented by the flux densities,
is
represented by the flux densities,
![]()
![]()
By varying the spectral dataset, we then produce simulated spectral
datasets
| |
(8) |
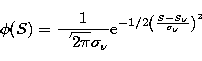 |
(9) |
For each simulated spectral dataset, we apply the ![]() -order (
-order (![]() ) polynomial fitting by the basis functions
) polynomial fitting by the basis functions ![]() , and
minimize the
, and
minimize the ![]() parameter of the fit
parameter of the fit
![\begin{displaymath}
\chi^2 = \sum^N_{i=1}\frac{1}{\sigma^2_i}\left[ (S_{\rm sym})_i -
\sum^{M}_{k=0} A_k X_k(\nu_i) \right]^2,\end{displaymath}](/articles/aas/full/1998/17/ds7109/img94.gif) |
(10) |
![\begin{displaymath}
A_j = \sum^M_{k=0} [a]^{-1}_{jk} \beta_k, \quad \sigma^2(A_j) =
[a]{-1}_{jj} \,.\end{displaymath}](/articles/aas/full/1998/17/ds7109/img95.gif) |
(11) |
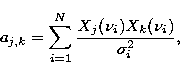
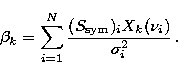
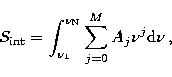 |
(12) |
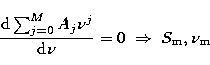 |
(13) |
![\begin{figure}
\centering
\includegraphics[width=8.8cm]{7109f8.eps}\end{figure}](/articles/aas/full/1998/17/ds7109/Timg107.gif) |
Figure 8: Curvature correction coefficients derived from simulating synchrotron spectra and subsequent fitting them by the polynomial functions described in Sect. 5.4 |
The local curvature of spectral fits is:
![\begin{displaymath}
\kappa = \frac{{\rm d}^2 S}{{\rm d}\nu^2} \left[1+\left(\frac{{\rm d}S}{{\rm d}\nu}\right)^2
\right]^{-1/3}\, .\end{displaymath}](/articles/aas/full/1998/17/ds7109/img108.gif) |
(14) |
| |
(15) |
An alternative method to estimate ![]() is to
determine it numerically, by simulating the synchrotron spectrum with
given turnover frequency and spectral index, and fitting it by the
polynomial functions used in Sect. 5.4. We have performed
such calculations, using the spectral form described in
Sect. 5.1, and covering a range of turnover frequencies and
spectral indices. The results are shown in Fig. 8 in which
the ratio of fitted values to the theoretical values of the turnover
frequency is plotted against the synchrotron spectral index. The contours
show different values of
is to
determine it numerically, by simulating the synchrotron spectrum with
given turnover frequency and spectral index, and fitting it by the
polynomial functions used in Sect. 5.4. We have performed
such calculations, using the spectral form described in
Sect. 5.1, and covering a range of turnover frequencies and
spectral indices. The results are shown in Fig. 8 in which
the ratio of fitted values to the theoretical values of the turnover
frequency is plotted against the synchrotron spectral index. The contours
show different values of ![]() . One can see that the determined ratios do
not depend strongly on the spectral index. Figure 8 can be used
for the same purpose of correcting the fitted turnover frequencies obtained
through the procedure described in Sect. 5.4.
. One can see that the determined ratios do
not depend strongly on the spectral index. Figure 8 can be used
for the same purpose of correcting the fitted turnover frequencies obtained
through the procedure described in Sect. 5.4.
![\begin{figure}
\includegraphics[width=5.8cm,angle=-90]{7109f9a.eps}
\hspace{6mm}...
...s}
\hspace{6mm}
\includegraphics[width=5.8cm,angle=-90]{7109f9d.eps}\end{figure}](/articles/aas/full/1998/17/ds7109/Timg118.gif) |
Figure 9:
Maps of 3C345 from the multi-frequency VLBA observation made
on June 24, 1995. The restoring beam is 1.2 |
Copyright The European Southern Observatory (ESO)