

Up: A strategy for fitting
We deduce from the above considerations that there are substantial
regions of the 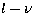 plane where attempts to fit independently all the peaks
in a given frequency range of a given (l,m) spectrum are likely to
fail; indeed, the region where such fitting is appropriate is a
relatively small fraction of the full
plane where attempts to fit independently all the peaks
in a given frequency range of a given (l,m) spectrum are likely to
fail; indeed, the region where such fitting is appropriate is a
relatively small fraction of the full 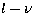 plane that is
accessible to measurements
from GONG or the MDI instrument
on SOHO. To make inferences about mode parameters outside this
region, we need to make some assumptions about the position and
relative strength of the leaked modes in the spectrum.
However, the
proper calculation of the leakage matrix at high degree is
computationally expensive.
The approach to mode-fitting described
here aims to work around this by fixing some of the parameters
of the fit in advance, using information obtained from the data
rather than a detailed leakage model.
plane that is
accessible to measurements
from GONG or the MDI instrument
on SOHO. To make inferences about mode parameters outside this
region, we need to make some assumptions about the position and
relative strength of the leaked modes in the spectrum.
However, the
proper calculation of the leakage matrix at high degree is
computationally expensive.
The approach to mode-fitting described
here aims to work around this by fixing some of the parameters
of the fit in advance, using information obtained from the data
rather than a detailed leakage model.
To illustrate the procedure, we shall concentrate on one
typical multiplet, that with l=150, n=4 in GONG month 4.
The first stage in the process is to locate the target system of peaks and
leaks, which forms one of the broad, slanted bands of power shown in the
greyscale plot in Fig. 7.
This requires only approximate knowledge of the m=0 frequency
of the target mode and its nearest neighbouring leaks (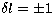 ),
and the linear part of the m-dependence arising from rotation.
Figure 10 shows the power in the region of interest in the
),
and the linear part of the m-dependence arising from rotation.
Figure 10 shows the power in the region of interest in the 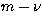 plane with the linear part of the rotational dependence taken out to show
the differential rotation more clearly. The data
are averaged over bands covering several m-values, and smoothed in
frequency, to clarify the structure.
Next we locate the
maximum of the smoothed data in each band as shown in the figure.
plane with the linear part of the rotational dependence taken out to show
the differential rotation more clearly. The data
are averaged over bands covering several m-values, and smoothed in
frequency, to clarify the structure.
Next we locate the
maximum of the smoothed data in each band as shown in the figure.
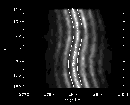 |
Figure 10:
Smoothed 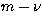 power spectrum of the n=4,l=150 mode and its leaks. The
linear part of the m-dependence of the frequencies has been removed.
The stars indicate maxima of the central ridge, and the curve shows
a polynomial fit through these maximum points. The parallel curves
indicate the frequency range, determined from the initial estimate of the
linewidth, in which the maximum is sought power spectrum of the n=4,l=150 mode and its leaks. The
linear part of the m-dependence of the frequencies has been removed.
The stars indicate maxima of the central ridge, and the curve shows
a polynomial fit through these maximum points. The parallel curves
indicate the frequency range, determined from the initial estimate of the
linewidth, in which the maximum is sought |
A better approximation to the m-dependence due to rotation can
be obtained from a third-order polynomial fit to the position of the smoothed maxima
as a function of m.
Then, taking this m-dependence into account, the individual m
spectra can be collapsed to form
a first approximation to the m-averaged spectrum.
Under standard assumptions that the modes are randomly and independently
excited with a white-noise forcing function, at each frequency point
the real and imaginary
parts of the Fourier transform of the individual-m time series
 will be normally distributed with zero mean. (This is
true even when leakage is taken into account, since the sum of independent
Normal variables is itself Normal.) Thus at each frequency point the
individual-m power spectra are proportional to a chi-squared variable with
two degrees of freedom. (Of course, as discussed in more detail by
Appourchaux et al. 1998, in the presence of leakage the
different individual-m spectra will not in general be independent.)
will be normally distributed with zero mean. (This is
true even when leakage is taken into account, since the sum of independent
Normal variables is itself Normal.) Thus at each frequency point the
individual-m power spectra are proportional to a chi-squared variable with
two degrees of freedom. (Of course, as discussed in more detail by
Appourchaux et al. 1998, in the presence of leakage the
different individual-m spectra will not in general be independent.)
Since there are 2l+1 individual m spectra for a given l,
and notwithstanding the fact that the errors in each spectrum may not be
entirely independent,
we assume that by the Central Limit Theorem the
errors in the m-averaged spectrum
for high l approach a normal distribution, and we proceed to
fit the spectrum
using a non-linear least-squares method in which the variance at each
frequency point is approximated as being proportional to the data
value divided by the number of spectra averaged.
The algorithm used is based on the CURFIT routine of Bevington (1969).
The model consists of seven peaks -- the target and the leaks out to
 -- of equal width, evenly spaced and with the relative
powers of the leaks forced to be symmetrical, on a flat background, as
illustrated in Fig. 11. The peak profile is assumed to be Lorentzian,
defined by
-- of equal width, evenly spaced and with the relative
powers of the leaks forced to be symmetrical, on a flat background, as
illustrated in Fig. 11. The peak profile is assumed to be Lorentzian,
defined by
| 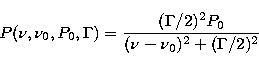 |
(10) |
where  is the central frequency of the peak,
is the central frequency of the peak,
 the FWHM and P0 the maximum height of the peak;
the FWHM and P0 the maximum height of the peak;  is
frequency.
The full model for the m-averaged spectrum is thus given by
is
frequency.
The full model for the m-averaged spectrum is thus given by
| ![\begin{displaymath}
T(\nu,\nu_0) = \sum_{\delta l=-3}^3 P[\nu,\nu_0-\delta l \times \delta\nu,
P_0(\vert\delta l\vert),\Gamma]+B_0,\end{displaymath}](/articles/aas/full/1998/15/ds1466/img109.gif) |
(11) |
where  is the spacing (assumed uniform)
between the peaks, B0 is the background
level of the power, and
is the spacing (assumed uniform)
between the peaks, B0 is the background
level of the power, and 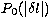 is the power of each
ridge, which in this symmetric model depends only on
is the power of each
ridge, which in this symmetric model depends only on 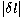 .Thus we determine eight constants -
.Thus we determine eight constants -  ,
,  ,
,  ,B0 and four amplitudes P0(0,1,2,3) - which together define
the fitted model
,B0 and four amplitudes P0(0,1,2,3) - which together define
the fitted model  .
.
 |
Figure 11:
The m-averaged spectrum of the l=150,n=4 mode (crosses) after removal of a third-order polynomial approximation to
the m-dependence due to rotation. The continuous curve shows the fit
of a symmetrical model comprising 7 equally spaced Lorentzian peaks.
The units of power are arbitrary |
This  , which has been obtained by fitting
the m-averaged spectrum, then becomes the "template''
used to fit to the individual-m spectra. To each m spectrum
we fit a model,
, which has been obtained by fitting
the m-averaged spectrum, then becomes the "template''
used to fit to the individual-m spectra. To each m spectrum
we fit a model,
| ![\begin{displaymath}
P(\nu,m)=A_{\rm T}(m)T[\nu,\nu_{\rm T}(m)]+B_{\rm T}(m)\;,\end{displaymath}](/articles/aas/full/1998/15/ds1466/img114.gif) |
(12) |
with the vertical scale 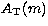 , background
level
, background
level 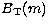 and central frequency
and central frequency 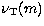 as the only free parameters. As already stated, we assume that each point of
the spectrum is proportional to a chi-squared random variable with
two degrees of freedom. The fit is then obtained by minimizing
as the only free parameters. As already stated, we assume that each point of
the spectrum is proportional to a chi-squared random variable with
two degrees of freedom. The fit is then obtained by minimizing
| 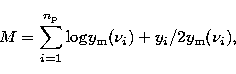 |
(13) |
where the index i runs over the number 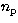 of data points in the
fitting region (which extends roughly 10 times
of data points in the
fitting region (which extends roughly 10 times  either side of the
central frequency),
either side of the
central frequency),
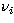 and yi are the values of the frequency and the power at each point in
the fitting region, and
and yi are the values of the frequency and the power at each point in
the fitting region, and
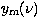 is the model function. This is equivalent to maximizing
the likelihood function, given the assumed
chi-squared statistics. (See Anderson
et al. 1990, for a discussion of this kind of fitting.)
Any reasonable minimization technique can be used; in the example
followed here, we used an IDL version of the DFPMIN routine from
Press et al.
(1989).
is the model function. This is equivalent to maximizing
the likelihood function, given the assumed
chi-squared statistics. (See Anderson
et al. 1990, for a discussion of this kind of fitting.)
Any reasonable minimization technique can be used; in the example
followed here, we used an IDL version of the DFPMIN routine from
Press et al.
(1989).
From these crude fits we obtain an improved approximation to the
m-dependence of the splitting
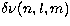 , defined by
, defined by
|  |
(14) |
which is
sufficient to provide a starting point for
the iteration of more realistic fits.
We next approximate the splitting as a function of m with a sum
of Legendre polynomials Pi(m/L),
where L=l+1/2,
containing 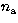 odd and even terms:
odd and even terms:
| 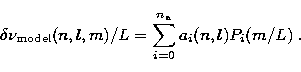 |
(15) |
This expression for  is used in turn
to recompute the collapse of the individual m spectra and yields
an improved m-averaged spectrum.
is used in turn
to recompute the collapse of the individual m spectra and yields
an improved m-averaged spectrum.
In the next iteration, the template is obtained by fitting
the m-averaged spectrum with a
model that allows the leaks to have independent width, relative power and
spacing, so that the template is given by
| ![\begin{displaymath}
T(\nu,m)=\sum_{\delta l=-3}^3 P[\nu,\nu_0-\delta\nu(\delta l),
P_0(\delta l),\Gamma(\delta l)]+B_0,\end{displaymath}](/articles/aas/full/1998/15/ds1466/img126.gif) |
(16) |
where 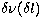 is now the separation of each ridge from the
central frequency (for
is now the separation of each ridge from the
central frequency (for 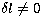 ).
Thus we now determine a central frequency
).
Thus we now determine a central frequency  ,
six constants
,
six constants  , seven constants
P0, seven constants
, seven constants
P0, seven constants  and one background.
Furthermore, the fitting is done separately over three ranges
of m, to allow some variation with m of the leak power and spacing.
This is illustrated in Fig. 12.
The existence of such variation can be deduced even from a simplified
version of the leakage calculation. The spacing variation arises because
each leaked "peak" is really a doublet with
and one background.
Furthermore, the fitting is done separately over three ranges
of m, to allow some variation with m of the leak power and spacing.
This is illustrated in Fig. 12.
The existence of such variation can be deduced even from a simplified
version of the leakage calculation. The spacing variation arises because
each leaked "peak" is really a doublet with  peaks,
separated by about 2a1, where a1 is the leading rotational
splitting coefficient as in Eq. (15).
The strength of the two leaks varies, as illustrated in Fig. 3;
and so as m goes from -l to l the main contribution to the power
in the ridge shifts from the component that is farther from the target (l,m)
to the one that is closer. Similar arguments apply to the leaks with
peaks,
separated by about 2a1, where a1 is the leading rotational
splitting coefficient as in Eq. (15).
The strength of the two leaks varies, as illustrated in Fig. 3;
and so as m goes from -l to l the main contribution to the power
in the ridge shifts from the component that is farther from the target (l,m)
to the one that is closer. Similar arguments apply to the leaks with
 , though these leaks are triplets rather than doublets.
Dividing the fits in this way does not appear to introduce any noticeable
discontinuities in the results; the division was chosen after consideration
both of the simple leakage model behaviour discussed above and the
behaviour of the real data.
, though these leaks are triplets rather than doublets.
Dividing the fits in this way does not appear to introduce any noticeable
discontinuities in the results; the division was chosen after consideration
both of the simple leakage model behaviour discussed above and the
behaviour of the real data.
 |
Figure 12:
The m-averaged spectra (symbols) for the l=150,n=4 mode, showing fits (solid curve)
to a seven-peak
model where all peaks have independent parameters, for a) 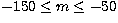 ,b) ,b) 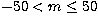 , and c) , and c) 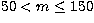 |
Each template is then used as before over the appropriate range
of m to obtain the final frequencies.
Figure 13 shows the final splittings derived for our multiplet, again
with the linear m-dependence removed to show the curvature.
 |
Figure 13:
Splittings  , as defined in Eq. (14),
for the l=150,n=4 multiplet, with linear m-dependence removed.
The solid curve shows the fitted , as defined in Eq. (14),
for the l=150,n=4 multiplet, with linear m-dependence removed.
The solid curve shows the fitted  as defined in
Eq. (15) as defined in
Eq. (15) |


Up: A strategy for fitting
Copyright The European Southern Observatory (ESO)
![]() ),
and the linear part of the m-dependence arising from rotation.
Figure 10 shows the power in the region of interest in the
),
and the linear part of the m-dependence arising from rotation.
Figure 10 shows the power in the region of interest in the ![]() plane with the linear part of the rotational dependence taken out to show
the differential rotation more clearly. The data
are averaged over bands covering several m-values, and smoothed in
frequency, to clarify the structure.
Next we locate the
maximum of the smoothed data in each band as shown in the figure.
plane with the linear part of the rotational dependence taken out to show
the differential rotation more clearly. The data
are averaged over bands covering several m-values, and smoothed in
frequency, to clarify the structure.
Next we locate the
maximum of the smoothed data in each band as shown in the figure.
![]() will be normally distributed with zero mean. (This is
true even when leakage is taken into account, since the sum of independent
Normal variables is itself Normal.) Thus at each frequency point the
individual-m power spectra are proportional to a chi-squared variable with
two degrees of freedom. (Of course, as discussed in more detail by
Appourchaux et al. 1998, in the presence of leakage the
different individual-m spectra will not in general be independent.)
will be normally distributed with zero mean. (This is
true even when leakage is taken into account, since the sum of independent
Normal variables is itself Normal.) Thus at each frequency point the
individual-m power spectra are proportional to a chi-squared variable with
two degrees of freedom. (Of course, as discussed in more detail by
Appourchaux et al. 1998, in the presence of leakage the
different individual-m spectra will not in general be independent.)
![]() -- of equal width, evenly spaced and with the relative
powers of the leaks forced to be symmetrical, on a flat background, as
illustrated in Fig. 11. The peak profile is assumed to be Lorentzian,
defined by
-- of equal width, evenly spaced and with the relative
powers of the leaks forced to be symmetrical, on a flat background, as
illustrated in Fig. 11. The peak profile is assumed to be Lorentzian,
defined by
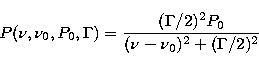
![\begin{displaymath}
T(\nu,\nu_0) = \sum_{\delta l=-3}^3 P[\nu,\nu_0-\delta l \times \delta\nu,
P_0(\vert\delta l\vert),\Gamma]+B_0,\end{displaymath}](/articles/aas/full/1998/15/ds1466/img109.gif)
![]() , which has been obtained by fitting
the m-averaged spectrum, then becomes the "template''
used to fit to the individual-m spectra. To each m spectrum
we fit a model,
, which has been obtained by fitting
the m-averaged spectrum, then becomes the "template''
used to fit to the individual-m spectra. To each m spectrum
we fit a model,
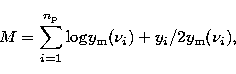
![]() , defined by
, defined by

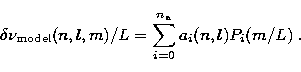
![\begin{displaymath}
T(\nu,m)=\sum_{\delta l=-3}^3 P[\nu,\nu_0-\delta\nu(\delta l),
P_0(\delta l),\Gamma(\delta l)]+B_0,\end{displaymath}](/articles/aas/full/1998/15/ds1466/img126.gif)

