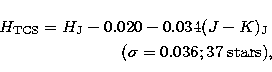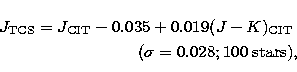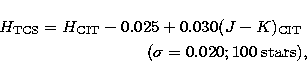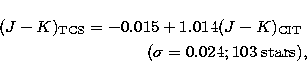Up: Broad-band JHK(L') photometry of
Subsections
The observations were made over eight different periods distributed all
through 1994-1997, with the 1.54 m. Carlos Sánchez Telescope (TCS
system).
The procedure adopted during the observations is as follows.
Several pairs of calibration stars, one ascending and the other descending,
were tracked all through each run over an airmass range 1-2. The reduction
procedure consisted of the iterative application of the following equation to
the set of calibration stars:
|  |
(1) |
where  and
and 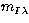 are respectively the calibration and
instrumental monochromatic magnitudes observed for
a source star at an airmass Z and time UT,
are respectively the calibration and
instrumental monochromatic magnitudes observed for
a source star at an airmass Z and time UT, 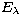 is the extinction
coefficient at wavelength
is the extinction
coefficient at wavelength 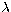 ,
,  accounts for the temporal drift, and
accounts for the temporal drift, and 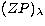 is the instrumental zero point. In this way,
Bouguer lines were obtained every night. There was a considerable
overlap in the standard and programme stars observed in different
runs, in order to prevent zero-point differences between them. Two
different impedances were used in the amplifier system of the photometer, the low impedance
mode was adopted to measure in L' and bright stars (
is the instrumental zero point. In this way,
Bouguer lines were obtained every night. There was a considerable
overlap in the standard and programme stars observed in different
runs, in order to prevent zero-point differences between them. Two
different impedances were used in the amplifier system of the photometer, the low impedance
mode was adopted to measure in L' and bright stars (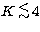 mag) in JHK; however
the high impedance mode was adopted in JHK measurements for faint stars (
mag) in JHK; however
the high impedance mode was adopted in JHK measurements for faint stars (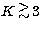 mag) in
order to minimize the noise.
mag) in
order to minimize the noise.
In Table 1, we list the calibration stars observed during the
campaign. As can be appreciated, they cover a wide magnitude range
(0 mag 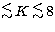 mag) and in spectral types (late B to early M) which match
properly the composition of our sample.
In Table 2 we present the JHK(L') magnitudes of the programme
stars (approximately 2500 measurements in JHK and 700 in L' including
calibration)
mag) and in spectral types (late B to early M) which match
properly the composition of our sample.
In Table 2 we present the JHK(L') magnitudes of the programme
stars (approximately 2500 measurements in JHK and 700 in L' including
calibration)![[*]](/icons/foot_motif.gif) . When
there were more than two measurements, the JHKL' magnitudes
are the average of the observations in each waveband. In Fig.
2, we display the histograms of the residuals of the
stars measured more than twice (approximately 75% of the sample). The mean
internal consistency of measurements in J,H and K is around 0.02 mag,
and 0.03 - 0.04 mag for L'.
The amount of data presented is enough to provide a preliminary qualitative
analysis of the extinction in the near-IR bands at the Observatorio del
Teide.
. When
there were more than two measurements, the JHKL' magnitudes
are the average of the observations in each waveband. In Fig.
2, we display the histograms of the residuals of the
stars measured more than twice (approximately 75% of the sample). The mean
internal consistency of measurements in J,H and K is around 0.02 mag,
and 0.03 - 0.04 mag for L'.
The amount of data presented is enough to provide a preliminary qualitative
analysis of the extinction in the near-IR bands at the Observatorio del
Teide.
In Fig. 3, we show the correlation between the extinction coefficients
in the three different bands. The relations are as follows:
| 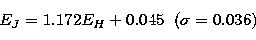 |
(2) |
|  |
(3) |
|  |
(4) |
We have considered the average of the least squares fits of the x-axis versus the y-axis, and the y-axis versus the x-axis, in order to determine the slope of the linear fit more accurately.
The relation in L' is very uncertain because no measurements of EL' were
made in high-extinction conditions.
The consistency with the previous relations
derived in Alonso et al. (1994b; Paper II) is noteworthy. If one adopts extinction in H band as baseline for the comparisons
(since this is the cleanest band) then the intercepts in the extinction plots
for J and K bands versus H band are positive (as
deduced from Eqs. (2) and (3)), which would imply a
non-zero aerosol extinction (0.045 mag for J and 0.036 mag for K).
As regard L', the intercep has a lesser level of confidence, given that there are no high
extinction values of L'. By considering the above relations, the decrease in
extinction from 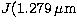 ) to H(1.648
) to H(1.648 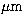 ) to
K(2.186
) to
K(2.186 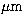 )to L'(3.690
)to L'(3.690 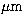 ) is in the ratio 1.172:1:0.868:0.645.
If we fit these data to a law of the form
) is in the ratio 1.172:1:0.868:0.645.
If we fit these data to a law of the form 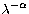 ,
we get
,
we get 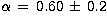 . This value is in agreement with
the values quoted by Hayes & Latham (1975)
as measured in the optical range in different astronomical observatories,
which ranges between
. This value is in agreement with
the values quoted by Hayes & Latham (1975)
as measured in the optical range in different astronomical observatories,
which ranges between  and
and 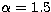 .
.
![\begin{figure}
\begin{center}
\includegraphics[height=21cm]{ds7035f2.eps}\end{center} \end{figure}](/articles/aas/full/1998/14/ds7035/Timg32.gif) |
Figure 2:
Residuals of the observed magnitudes in each filter. Note that
the axis scales are different for L' according to the small number of
measurements made with this filter |
If we take as fiducial values for the extinction in the near-IR bands
between 1 and 2 air masses
those reported by Manduca & Bell (1979)
and Volk et al. (1989), which would correspond to dust free nights with 2 to 10 mm of precipitable water vapour
(i.e. EJ 0.07 - 0.10, EH 0.04 - 0.06
and EK 0.05 - 0.08), roughly 35% of the nights are within these conditions (J: 34%, H: 38% and
K: 35%). Furthermore, only  20% of the nights show strong
extinction (E>0.2 in J, E>0.15 in H and K). As for L', the
typical extinction lies within the range 0.07 - 0.15.
In general, large extinction values in spring are mainly caused by water vapour absorption;
however in summer, they are connected with the dust transported over the
observatory by southerly winds from the Sahara desert (an atmospheric
phenomenon known locally as calima).
20% of the nights show strong
extinction (E>0.2 in J, E>0.15 in H and K). As for L', the
typical extinction lies within the range 0.07 - 0.15.
In general, large extinction values in spring are mainly caused by water vapour absorption;
however in summer, they are connected with the dust transported over the
observatory by southerly winds from the Sahara desert (an atmospheric
phenomenon known locally as calima).
In summary, this concise analysis supports the good quality of the
Observatorio del Teide for near-infrared observations.
![\begin{figure}
\begin{center}
\includegraphics[height=10.8cm]{ds7035f3.eps}\end{center} \end{figure}](/articles/aas/full/1998/14/ds7035/Timg33.gif) |
Figure 3:
The correlation between extinction coefficients in the different
bands measured at the Observatorio del Teide (TCS System). The straight
lines correspond to the fits obtained (Sect. 3). Note the consistency of
the relation for high extinction values, this point grants the
reliability of colours obtained even in dusty conditions |
The differences in the atmospheric transmission at each site and the absence of
standard infrared filters make transformation
equations necessary in order to homogenize magnitudes measured in different systems.
Since the previous work which established the TCS system
(Kidger 1992;
Alonso et al. 1994a Paper I; and Paper II), we have made an effort to increase the number of stars common with other near-IR photometric systems. For the first time we also
include L' magnitudes.
We present the re-calculated transformations for magnitudes
and colours into/from the systems of Johnson
(Johnson et al. 1966;
Johnson et al. 1968;
Lee 1970), ESO
(Bouchet et al. 1991), CIT and
Selby et al. (1988) narrow band. It is noteworthy that the
ranges of validity of the transformations has been extended in colour.
As expected, the dispersion of the correlations has decreased with the
increase in the number of stars compared to previous ones. We show
the residuals between the transformed and observed TCS magnitudes in
order to assess the linearity of the TCS system (Fig. 4). No appreciable departures from zero are noted in the residuals of the transformed
magnitudes (except for H values which are probably caused by the somewhat
poor definition of this band in the Jonhnson system).
This ensures the linearity of the TCS system over the range -3 mag <K<10.5 mag.
![\begin{figure}
\begin{center}
\includegraphics[height=10.8cm]{ds7035f4.eps}\end{center} \end{figure}](/articles/aas/full/1998/14/ds7035/Timg34.gif) |
Figure 4:
Residuals of the differences between the magnitudes measured
at the Observatorio del Teide, and the magnitudes transformed from the
different photometric systems by using the equations of Sect. 3. Open circles:
Johnson system; triangles: ESO system; hexagons: CIT system, and
squares: Selby et al. (1988) |
From a historical point of view the first photometric measurements in the
near IR windows were made by Johnson (1966). The large number of measurements
of some of his standards makes of this system a necessary reference for comparison. For the definition of
H-band of Johnson system we have considered
the works by Johnson et al. (1968)
and Lee (1970), and the transformations
provided by Bessell & Brett (1988). We
have made an effort to almost double the number of stars common to both
the TCS and the Johnson systems.
|  |
(5) |
| |
| 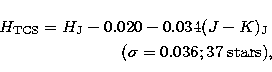 |
(6) |
| |
|  |
(7) |
| |
|  |
(8) |
| |
|  |
(9) |
| |
|  |
(10) |
| |
|  |
(11) |
| |
|  |
(12) |
| |
These transformations are applicable in the range 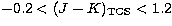 ,
,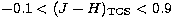 ,
,  and
and 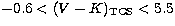 .
.
In order to understand the above transformation equations in terms of the
passband profiles available in literature for both the TCS and Johnson
systems, we have synthesized IR colours by using Kurucz's models properly sampling gravity, metallicity and effective temperature. For the synthesis
of colours we have followed the procedure described in Paper I and
Alonso et al. (1995). In Fig. 5, we show the confrontation of the synthetic lines obtained for both systems overimposed on the TCS-colour vs. Johnson-colour diagrams.
The mean trends of the synthetic colours reproduce fairly well the loci
of the stars considered to establish the transformations, reinforcing
the validity of them.
![\begin{figure}
\begin{center}
\includegraphics[height=10.8cm]{ds7035f5.eps}\end{center}
\end{figure}](/articles/aas/full/1998/14/ds7035/Timg47.gif) |
Figure 5:
Infrared colours of the TCS system versus infrared
colours of Johnson system. The squares correspond to stars common
to both systems.
The lines correspond to the synthetic colours
obtained by using Kurucz models and the passband of profiles of the
filters of each system |
The CIT system is described in
Elias et al. (1982)
and Frogel et al. (1978).
Carney (1983a,b) also provides a number of stars in this system. The derived equations for magnitudes are:
| 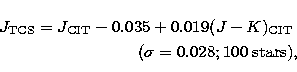 |
(13) |
| |
| 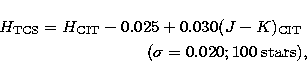 |
(14) |
| |
|  |
(15) |
| |
and the corresponding colour transformations:
| 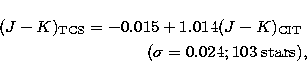 |
(16) |
| |
|  |
(17) |
| |
|  |
(18) |
| |
The applicability of these transformations is restricted to the following
colour ranges: 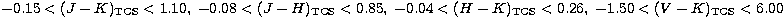 .The transformations to CIT are excellent. The small colour
terms and the low dispersion show that both systems share very similar filters.
The good agreement with Carney's dwarf data is noteworthy. The slightly high dispersion in J is probably due to the water vapour absorption bands which
flank this window.
Selby et al. (1988) provide high quality photometry for a list of bright stars
(measured with a set of
narrow-band filters specially designed to avoid the edges of the atmospheric
absorption bands and the presence of telluric lines). By using the stars common to both systems we have
re-derived the transformations, whose small dispersion reflects the good level of accuracy
of the TCS standard system.
.The transformations to CIT are excellent. The small colour
terms and the low dispersion show that both systems share very similar filters.
The good agreement with Carney's dwarf data is noteworthy. The slightly high dispersion in J is probably due to the water vapour absorption bands which
flank this window.
Selby et al. (1988) provide high quality photometry for a list of bright stars
(measured with a set of
narrow-band filters specially designed to avoid the edges of the atmospheric
absorption bands and the presence of telluric lines). By using the stars common to both systems we have
re-derived the transformations, whose small dispersion reflects the good level of accuracy
of the TCS standard system.
|  |
(19) |
| |
|  |
(20) |
| |
|  |
(21) |
| |
|  |
(22) |
| |
These transformations are applicable in the range 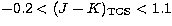 ,
,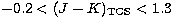 and
and  .
.
Bouchet et al. (1991) have redefined the ESO system after the instrumental change
at La Silla. They provide a list of 199 standard stars to an accuracy of 0.02
mag. Given the importance of comparing TCS system with a southern
hemisphere system, we have doubled the number of common stars with respect to
Paper II, thereby tightening the relations obtained and extending the colour ranges.
The strong colour term for the J transformation, which
only can be explained by assuming different effective wavelengths for
this band in both systems, is remarkable.
|  |
(23) |
| |
|  |
(24) |
| |
|  |
(25) |
| |
|  |
(26) |
| |
The transformations for colours are:
|  |
(27) |
| |
|  |
(28) |
| |
|  |
(29) |
| |
|  |
(30) |
| |
The applicability of these transformations is restricted to the following
colour ranges: 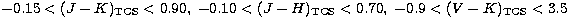 , and
, and
 .
.
The transmission of the J, H and K bands has been described in Paper II.
Here we present the transmission of the L' filter (Table 3). The experimental
arrangement for this measurement was the same as that adopted for the
J, H and K filters.
Although the L' filter of the TCS system has been somewhat optimized (i.e. it is not so broad
as the original L filter of the Johnson system, and partly avoids the most opaque
region of the L window), it can be appreciated
that it is strongly affected by the water vapour bands absorption which plague this
wavelength range. This is why the number of measurements
in L' is less than in JHK, as the total number of useful nights is correspondingly smaller. Also for this reason the
correlation between extinction in J and L' is somewhat more difficult to
establish, as it
is mainly related to water vapour absorption instead of the aerosol
component. The absolute calibration of the L' (and also that of the JHK) photometry has been
linked to Vega (BS7001) following the method described in Paper I.


Up: Broad-band JHK(L') photometry of
Copyright The European Southern Observatory (ESO)
![\begin{figure}
\begin{center}
\includegraphics[height=21cm]{ds7035f2.eps}\end{center} \end{figure}](/articles/aas/full/1998/14/ds7035/Timg32.gif)
![]() 20% of the nights show strong
extinction (E>0.2 in J, E>0.15 in H and K). As for L', the
typical extinction lies within the range 0.07 - 0.15.
In general, large extinction values in spring are mainly caused by water vapour absorption;
however in summer, they are connected with the dust transported over the
observatory by southerly winds from the Sahara desert (an atmospheric
phenomenon known locally as calima).
20% of the nights show strong
extinction (E>0.2 in J, E>0.15 in H and K). As for L', the
typical extinction lies within the range 0.07 - 0.15.
In general, large extinction values in spring are mainly caused by water vapour absorption;
however in summer, they are connected with the dust transported over the
observatory by southerly winds from the Sahara desert (an atmospheric
phenomenon known locally as calima).