

Up: Broad-band JHK(L') photometry of
In Fig. 6 we show different IR diagrams derived from the
data of the present observational programme (given in Table 2). The internal consistency of the derived colours given the
small scatter around the average loci in all diagrams (discarding obviously
a few individual measurements) is noteworthy. The dispersion in the (H-K) colour may account for an effect of
metallicity similar to that found for main sequence stars (Paper II).
The similarity between the (J-L) : (H-L) and (V-K) : (U-V) diagrams supports
this possibility.
The absence of stars at the turn-over of the (H-K):(J-H) diagram shows that
the biasing of the sample with late K and M dwarfs is practically
negligible. Discrepancies in the mean trends of solar metallicity
lines published by other authors are seen. These could be ascribed partly
to the uncertainty of the transformations applied in this work; however,
zero-point and/or calibration problems in the definition of those photometric systems should not be completely discarded.
![\begin{figure}
\begin{center}
\includegraphics[height=10.8cm]{ds7035f6.eps}\end{center}
\end{figure}](/articles/aas/full/1998/14/ds7035/Timg72.gif) |
Figure 6:
Infrared colour diagrams for the stars of the sample measured at
the Observatorio del Teide. Solid circles : stars measured more than twice;
open circles: stars measured once; triangles: TCS standards
taken from Kidger (1992). The superimposed lines correspond to the
intrinsic relation extracted from literature and transformed to the
TCS system. Solid line: Bessel & Brett (1988); dashed line:
Bouchet et al. (1991) |
In
order to ascertain the influence of metallicity on near-IR colours we have plotted the (H-K):(J-H) diagram
for the whole sample, separating stars in three groups
of decreasing metallicity which roughly correspond to the
disk, halo/disk transition and halo populations (Fig. 7). The data of each of the groups in the range F5-K2
have been fitted, by using the least-squares
method, to straight lines of the form (H-K)=a+b(J-H). The group with
[Fe/H]  consists of 140 stars, in this case
the fit yields a=0.01 and b=0.19 with a rms error of 0.013 mag. The group
with
consists of 140 stars, in this case
the fit yields a=0.01 and b=0.19 with a rms error of 0.013 mag. The group
with  [Fe/H]
[Fe/H] 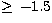 consists of 84 stars, in this case the fit yields a=-0.01 and b=0.22 with a rms error of 0.017 mag. The group with
consists of 84 stars, in this case the fit yields a=-0.01 and b=0.22 with a rms error of 0.017 mag. The group with
 [Fe/H] consists of 88 stars, in this case the fit yields a=-0.02 and b=0.25 with a rms error of 0.015 mag. It can be appreciated that the
slope of the mean traces increases slightly with decreasing metal content.
This effect is similar to that found for dwarf stars in Paper II. It is
probably related to the ion H-, which is the
dominant source of continuum opacity in the near infrared wavelength range for
the spectral types under consideration.
[Fe/H] consists of 88 stars, in this case the fit yields a=-0.02 and b=0.25 with a rms error of 0.015 mag. It can be appreciated that the
slope of the mean traces increases slightly with decreasing metal content.
This effect is similar to that found for dwarf stars in Paper II. It is
probably related to the ion H-, which is the
dominant source of continuum opacity in the near infrared wavelength range for
the spectral types under consideration.
![\begin{figure}
\begin{center}
\includegraphics[height=8.6cm]{7035f7.eps}\end{center} \end{figure}](/articles/aas/full/1998/14/ds7035/Timg81.gif) |
Figure 7:
(H-K):(J-H) diagram for the stars of the whole sample
separated according to metallicity.
Open circles: [Fe/H]  (Disk); squares: (Disk); squares:  [Fe/H] [Fe/H] 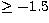 (Disk/Halo transition); triangles (Disk/Halo transition); triangles  [Fe/H]
(Halo). The
data in the range F5-K2 have been fitted to straight lines of the
form (J-H)=a+b(H-K). The mean lines obtained are overimposed on the graph
to show the sensitivity of IR colours to metallicity.
Solid line [Fe/H] [Fe/H]
(Halo). The
data in the range F5-K2 have been fitted to straight lines of the
form (J-H)=a+b(H-K). The mean lines obtained are overimposed on the graph
to show the sensitivity of IR colours to metallicity.
Solid line [Fe/H]  ; dashed line ; dashed line  [Fe/H] [Fe/H] 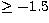 ; dotted line ; dotted line  [Fe/H] [Fe/H] |
Notice that the possible bias
of insterstellar reddening can be safely neglected in this analysis, since
on the one hand the size of the expected dereddening vectors is small, and on
the other, their direction is approximately parallel to the mean traces of the
giant stars on the (H-K) : (J-H) diagram.
In Table 4,
we provide the computed IR colours in the TCS system according to spectral type and luminosity class. For the computation of the mean colours we have
considered the photometric data of stars contained in Paper II and in the present
sample with reliable spectral classification.
Table 4:
Computed mean colours in the system of the TCS (Carlos Sánchez Telescope) for
giant and main sequence stars, separated according to spectral types
|
|
The interstellar extinction has not been taken into account, however most of the stars considered are population I giants with well determined
spectral types which are close to the solar neighbourhood.
We have adopted a rejection criteria in order to calculate the mean values,
for this reason the number of stars considered to obtain each colour varies slightly,
this is the cause of the small discrepancies observed when adding (J-H) and
(H-K) to obtain (J-K). The small differences between the mean lines of giants
and dwarfs are significant, indeed both lines should only strongly diverge
for types later than K3III ((V-K)>2.5).
Diagrams which combine optical and IR colours are suitable for analysing
separately the effects of effective temperature and metallicity.
In the (V-K):(B-V) diagram (Fig. 8) the spread under the intrinsic line
for population I stars is due mainly to the blanketing effect on the (B-V)
colour, since (V-K) is hardly sensitive to metallicity. We show
the mean lines for the giant branch of 47 Tuc ([Fe/H] 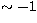 ) and
M 15 ([Fe/H]
) and
M 15 ([Fe/H] 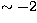 ). The different variation of the
(V-K) colour with metallicity when compared with that found for dwarf stars,
especially in the redder part of the diagrams (see Paper II), is remarkable. In
the (V-K):(U-V) diagram (Fig. 9) this point is even more conspicuous than in the (V-K):(B-V) diagram, although
a considerable number of stars in our sample lack U measurements. In this case, the
stretching of the metallicity axis is larger, since the blanketing effects
in the U band are stronger. Superimposed on the sample stars we show, for the
sake of comparison, the intrinsic lines for 47 Tuc
(Frogel et al. 1981), typical for disc globular clusters,
and the average for M 3, M 13, and M 92
(Cohen et al. 1978) as representative
of halo globular clusters. It is clear from this point that the different Galactic populations of
giant stars are well represented.
). The different variation of the
(V-K) colour with metallicity when compared with that found for dwarf stars,
especially in the redder part of the diagrams (see Paper II), is remarkable. In
the (V-K):(U-V) diagram (Fig. 9) this point is even more conspicuous than in the (V-K):(B-V) diagram, although
a considerable number of stars in our sample lack U measurements. In this case, the
stretching of the metallicity axis is larger, since the blanketing effects
in the U band are stronger. Superimposed on the sample stars we show, for the
sake of comparison, the intrinsic lines for 47 Tuc
(Frogel et al. 1981), typical for disc globular clusters,
and the average for M 3, M 13, and M 92
(Cohen et al. 1978) as representative
of halo globular clusters. It is clear from this point that the different Galactic populations of
giant stars are well represented.
![\begin{figure}
\begin{center}
\includegraphics[height=8.6cm]{ds7035f8.eps}\end{center} \end{figure}](/articles/aas/full/1998/14/ds7035/Timg85.gif) |
Figure 8:
(V-K):(B-V) diagram for the stars of the sample. The
superimposed lines correspond to the intrinsic relation extracted from
Johnson (1966) for Population I giants. Black circles correspond to stars with
IR colours measured in the present work; the remaining symbols correspond
to stars taken from the sources described in Sect. 2. Dotted line: intrinsic line for 47 Tuc
(Martínez-Roger 1985). Dashed line: intrinsic line for M 15
(Martínez-Roger 1985) |
![\begin{figure}
\begin{center}
\includegraphics[height=8.6cm]{ds7035f9.eps}\end{center}
\end{figure}](/articles/aas/full/1998/14/ds7035/Timg86.gif) |
Figure 9:
(V-K):(U-V) diagram for the stars of the sample. The
superimposed lines correspond to the intrinsic relation extracted from
Johnson (1966) for Population I giants. Black circles correspond to stars with
IR colours measured in the present work; the remining symbols correspond
to stars taken from the sources described in Sect. 2. This diagram provides an instructive
characterization of the sample insofar as the (V-K) axis reflects the extension in temperature, and the (U-V) axis the blanketing effect associated with the metal
abundance of stars |


Up: Broad-band JHK(L') photometry of
Copyright The European Southern Observatory (ESO)
![\begin{figure}
\begin{center}
\includegraphics[height=8.6cm]{7035f7.eps}\end{center} \end{figure}](/articles/aas/full/1998/14/ds7035/Timg81.gif)

![\begin{figure}
\begin{center}
\includegraphics[height=8.6cm]{ds7035f8.eps}\end{center} \end{figure}](/articles/aas/full/1998/14/ds7035/Timg85.gif)
![\begin{figure}
\begin{center}
\includegraphics[height=8.6cm]{ds7035f9.eps}\end{center}
\end{figure}](/articles/aas/full/1998/14/ds7035/Timg86.gif)