4 An example

To illustrate the suitability of our approach, we used recently published measurements of HR 466. Our initial plan was to recover an orbit consistent with those already published.

Towards this goal, we use the radial velocities published by Tokovinin (1993) and the interferometric measurements stored in the CHARA database Hartkopf et al. (1997): 28 interferometric observations and 8 radial velocities measurements for each components.

The initial guess is randomly chosen in the working space. An initial disjoint determination is required if one wants to check the consistency of different data sets. Such a determination would also help (but is not mandatory at all) to fix a first guess for the standard deviations of the residuals.

  

Table 1: Orbital parameters and their standard deviations of HR 466 obtained with our approach and those lately published

  

Table 2: Upper triangle of the correlation matrix of the orbital parameters of HR 466

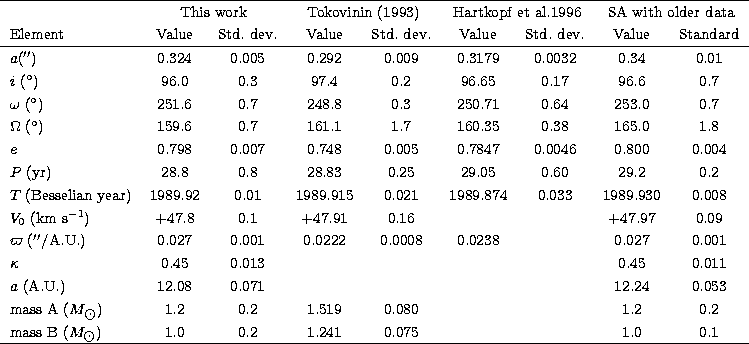
Using successively global and local search methods, we obtain the elements given in Table 1 (second and third columns) and the corresponding correlation matrix (Table 2).

  

Figure 1: Visual orbit and radial velocity curves of HR 466. In the spectroscopic plot, the open squares denote the measured radial velocities of B and the filled circles those of A

For that matrix, all the components corresponding to i, $\omega$ and $\Omega$ are computed with these angles expressed in radians. The standard errors of the different residuals are given in Table 3.

  

Table 3: Summary of the residuals using our orbit of HR 466. The hat (super) stands for the adjusted (observed) quantity

The difference of the residual variances between the spectroscopic components A and B is confirmed in Fig. 1. The covariance matrix (from which the standard deviations of the parameters and the correlation matrix are deduced) is computed by inverting the Fisher matrix (almost the Hessian matrix) at the minimum Pourbaix (1994); Press et al. (1992).

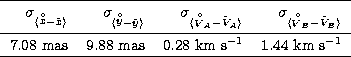These residuals are the result of three iterations of the complete minimization scheme. At the first iteration, the values of $\sigma_{x_j}$, $\sigma_{y_j}$, $\sigma_{V_{A_k}}$ and $\sigma_{V_{B_l}}$ (Eq. 17) had been fixed to a too low value. The residuals at the global minimum were used to estimate new values for these $\sigma_.$ and a new minimization was started. After two iterations of this minimization process, the variances at minimum were close enough to the estimated ones.

The efficiency Eichhorn (1989) is 0.51 which indicates a low correlation between the parameters. Even if we are dealing with few radial velocities, the visual orbit constrains the overall solution well enough.

How are our orbital parameters with respect to those recently published? Table 1 gives the orbital parameters and their standard deviations after Tokovinin (1993) and Hartkopf et al.1996. With a combined determination of the orbital parameters, Tokovinin gets a parallax of 22.2 mas (equivalent to a distance of 45 pc) and a mass sum of 2.76 $M_{\hbox{$\odot$}}$. In their paper, Hartkopf et al. adopt a distance of 42 pc which yields a mass sum of 2.8 $M_{\hbox{$\odot$}}$.

From the combination of Tokovinin's radial velocities and Hartkopf et al. visual observations, we obtain a parallax of 26.80 mas (corresponding to a distance of 37.31 pc) and a mass sum of only 2.20 $M_{\hbox{$\odot$}}$, which is quite different.

With the same data as used by Tokovinin (1993) for the radial velocities as well as for the visual observations, we obtain the orbital parameters given in the sixth column of Table 1. Here also, we obtain a parallax of 27 mas (which corresponds to a distance of 36.03 pc) and 2.2 $M_{\hbox{$\odot$}}$ for the mass sum. Our two determinations are consistent: in both cases, we get a larger parallax and a lower mass sum than those published recently. A reason for the discrepancy might be that the observations weights are slightly different. We followed Morbey's procedure (1992) to fix the weights. Although it would be possible to associate different weigths to different observations of the same type, we fixed a weight for all x, one for all y, one for all V_A and one for all V_B. Discrepant observations do not get lower weights.

When compared with the results obtained by ESA (1997), $26.15\pm0.81$ mas, it seems our result is in very good agreement with the latter value.

In fact, it seems we got more than expected at the beginning. The orbit we propose is probably the best one based on the available observations, even if it does not fully agree with the orbits already published (mainly on the mass sum and the parallax of the system).