

Up: Metal-poor turnoff and subgiant
In a field of area 2.0 square degrees centered on 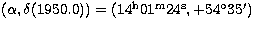 = (l,b) = (101
= (l,b) = (101 , +60
, +60 ),
a total of 1806 stars were measured with the Basel Iris photometer by one of
us (S.K.) from 15 48'' Palomar-Schmidt plates - i.e., 5 plates for each of
three RGU colors - taken by Purgathofer and Tammann in 1972. These
measurements were reduced to RGU magnitudes
using a photoelectric sequence which was established by Sandage and Tammann
(1974) and which extends down to limiting UBV magnitudes of 19.85, 19.49, and
18.76 magnitudes, respectively. The UBV data for the calibration
stars were converted to the standard RGU system via the transformation
equations calculated from a comprehensive grid of detailed flux distributions
of spectrophotometric standard stars by Buser (1978a,b).
),
a total of 1806 stars were measured with the Basel Iris photometer by one of
us (S.K.) from 15 48'' Palomar-Schmidt plates - i.e., 5 plates for each of
three RGU colors - taken by Purgathofer and Tammann in 1972. These
measurements were reduced to RGU magnitudes
using a photoelectric sequence which was established by Sandage and Tammann
(1974) and which extends down to limiting UBV magnitudes of 19.85, 19.49, and
18.76 magnitudes, respectively. The UBV data for the calibration
stars were converted to the standard RGU system via the transformation
equations calculated from a comprehensive grid of detailed flux distributions
of spectrophotometric standard stars by Buser (1978a,b).
Calibration curves could then be defined accurately down to limiting RGU
magnitudes of 18.07, 19.50, and 21.65 magnitudes, respectively, whence
instrumental RGU magnitudes and colors were derived for both the calibration
standard and the program stars. Although the number of calibration standard
stars is small and the residuals between their instrumental and standard
magnitudes as functions of instrumental color show considerable scatter,
the resulting color equations in Fig. 1 show the typical behavior
expected as resulting from minor mismatches of the photometric passbands behind
the instrumental and the standard systems. While the residuals for the two
longer-wavelength photometric passbands (G, R) can be well approximated by
linear equations,
those for the short-wavelength U-magnitude feature a characteristic
nonlinearity which is due to this near-UV passband's high sensitivity to the
strength of the Balmer lines and discontinuity (Buser 1978a, 1988).
Consequently, the corresponding color
equation has been approximated by a saw-tooth-like curve defined by three
contiguous linear segments of different slopes. Thus, the following color
equations were
adopted and applied in generating the final catalog of standard RGU data:
|  |
(1) |
|  |
(2) |
| 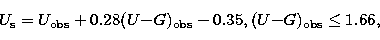 |
(3) |
| 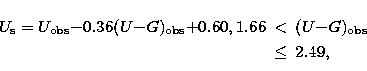 |
|
| (4) |
| 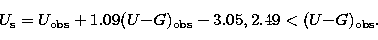 |
(5) |
Full details on the plate journal, the identification charts, and
the final photometric data will be published separately in the all-survey
catalogs for 14 fields of the Basel high-latitude program
(Buser et al. 1998b).
![\begin{figure}
\centering\includegraphics[width=8.8cm]{1475f1.eps}\end{figure}](/articles/aas/full/1998/14/ds1475/Timg9.gif) |
Figure 1:
Residuals between instrumental and standard magnitudes defining
the color Eqs. (1) through (5) which have been applied to
standardize the present catalog of field data |


Up: Metal-poor turnoff and subgiant
Copyright The European Southern Observatory (ESO)
![]() = (l,b) = (101
= (l,b) = (101![]() , +60
, +60![]() ),
a total of 1806 stars were measured with the Basel Iris photometer by one of
us (S.K.) from 15 48'' Palomar-Schmidt plates - i.e., 5 plates for each of
three RGU colors - taken by Purgathofer and Tammann in 1972. These
measurements were reduced to RGU magnitudes
using a photoelectric sequence which was established by Sandage and Tammann
(1974) and which extends down to limiting UBV magnitudes of 19.85, 19.49, and
18.76 magnitudes, respectively. The UBV data for the calibration
stars were converted to the standard RGU system via the transformation
equations calculated from a comprehensive grid of detailed flux distributions
of spectrophotometric standard stars by Buser (1978a,b).
),
a total of 1806 stars were measured with the Basel Iris photometer by one of
us (S.K.) from 15 48'' Palomar-Schmidt plates - i.e., 5 plates for each of
three RGU colors - taken by Purgathofer and Tammann in 1972. These
measurements were reduced to RGU magnitudes
using a photoelectric sequence which was established by Sandage and Tammann
(1974) and which extends down to limiting UBV magnitudes of 19.85, 19.49, and
18.76 magnitudes, respectively. The UBV data for the calibration
stars were converted to the standard RGU system via the transformation
equations calculated from a comprehensive grid of detailed flux distributions
of spectrophotometric standard stars by Buser (1978a,b).
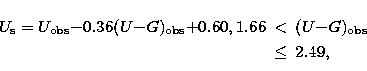
![\begin{figure}
\centering\includegraphics[width=8.8cm]{1475f1.eps}\end{figure}](/articles/aas/full/1998/14/ds1475/Timg9.gif)