

Up: Inversion of polarimetric data
In Sect. 3, we described
the B-G inverse in rather practical terms,
taking care to relate the description to the quantities obtained in, and
the concerns relevant to, real observations. Such a physical
understanding of the method is essential if it is to be used
properly, but we can obtain other insights into the method by
reexamining it in a more formal way![[*]](/icons/foot_motif.gif) .
.
Equation (4) above describes an operator  mapping an object from a
source space P into a data space D. Including noise
mapping an object from a
source space P into a data space D. Including noise  , we
have
, we
have
|  |
(A1) |
for  and
and  . Here P is a real Hilbert space,
parametrised by r, with a symmetric inner product
. Here P is a real Hilbert space,
parametrised by r, with a symmetric inner product

and D is a finite-dimensional Euclidean space with

We wish to make an estimate  of a single component
of the object u, based on the data f. To this end, we wish to
find a
of a single component
of the object u, based on the data f. To this end, we wish to
find a  (depending on r), such that
(depending on r), such that
|  |
(A2) |
We find this q as the solution of a minimisation problem.
Introducing the adjoint operator K*: 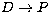 , and assuming
, and assuming
 , we have
, we have
|  |
(A3) |
Recalling that  , we see that
, we see that
 can be identified with the averaging kernel
can be identified with the averaging kernel
 , and that Eq. (A3) will be a good estimate of ur
when q is transformed by K* into the basis vector
, and that Eq. (A3) will be a good estimate of ur
when q is transformed by K* into the basis vector  corresponding to the component r of u. That is, Eq. (A3) would
be exact if K*q=er. The object K*q will instead be a linear
combination of basis vectors "close'' to er, and we can measure its
"scatter' around er with the operator
corresponding to the component r of u. That is, Eq. (A3) would
be exact if K*q=er. The object K*q will instead be a linear
combination of basis vectors "close'' to er, and we can measure its
"scatter' around er with the operator  such that
such that
 . Define
. Define
|  |
(A4) |
defining the (self-adjoint) operator 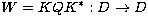 . We may also
define a measure of the stability of
. We may also
define a measure of the stability of  ,
,
|  |
(A5) |
by analogy with Eq. (11), where the operator  is such that
is such that
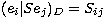 , where Sij is the positive definite
noise covariance
matrix.
The demand that
, where Sij is the positive definite
noise covariance
matrix.
The demand that  have unit area translates into the
constraint
have unit area translates into the
constraint  , where
, where  is the all-1 vector in P.
Writing
is the all-1 vector in P.
Writing 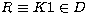 , this is equivalent to the constraint
, this is equivalent to the constraint
|  |
(A6) |
restricting q to a hypersurface in D, with normal R.
If we now introduce the functional  , such that
, such that
| ![\begin{displaymath}
c(q)\equiv \frac12 [\relax \mathcal{A}(q) + \lambda\relax \...
...cal{B}(q)]
=\frac12 \relax (q\vert(W+\lambda S)q)_{D},
\relax \end{displaymath}](/articles/aas/full/1998/13/ds6149/img120.gif) |
(A7) |
the minimisation problem becomes that of finding the q which
minimises c(q), subject to  .Considering small variations
.Considering small variations  in the hyperplane (that
is
in the hyperplane (that
is  , and defining the gradient
, and defining the gradient  (
( is self-adjoint since both W
and S are), we have
is self-adjoint since both W
and S are), we have

This is extremised at  such that
such that
 , and is a minimum if
, and is a minimum if
 .The operator S is positive-definite by definition, and the
operator W is positive-definite, since Q is. The operator c(q)
is therefore minimised when
.The operator S is positive-definite by definition, and the
operator W is positive-definite, since Q is. The operator c(q)
is therefore minimised when  , or
, or
|  |
(A8) |
for any 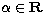 . Imposing the constraint Eq. (A6), we
thus find
. Imposing the constraint Eq. (A6), we
thus find
|  |
(A9) |
from which we can obtain Eq. (13), from the definition of
 .
.


Up: Inversion of polarimetric data
Copyright The European Southern Observatory (ESO)
![]() mapping an object from a
source space P into a data space D. Including noise
mapping an object from a
source space P into a data space D. Including noise ![]() , we
have
, we
have



![]() , such that
, such that
![\begin{displaymath}
c(q)\equiv \frac12 [\relax \mathcal{A}(q) + \lambda\relax \...
...cal{B}(q)]
=\frac12 \relax (q\vert(W+\lambda S)q)_{D},
\relax \end{displaymath}](/articles/aas/full/1998/13/ds6149/img120.gif)

