

Up: Inversion of polarimetric data
The Backus-Gilbert method is one of a family of methods for attacking
inverse problems. There are several general introductions to the
method (Parker 1977, gives an excellent review,
and Loredo & Epstein 1989, gives an example in an astrophysical
context) - we give a minimal introduction here, partly in order to
fix our notation. There is a more formal discussion of the method in
an appendix, and a thorough treatment can be found in Backus
& Gilbert (1970).
We wish to recover an underlying function u(r), in this case,
either an intensity, or the run of polarization with radius; the
parameter r here is the projected radial distance from the centre of the
eclipsed star's disk, in units where the star's radius is r=1. We
cannot measure this underlying function directly, but instead measure
an integral of it,  , which might be the observed luminosity or
polarisation of the eclipsed star. This is related to the
underlying function through
, which might be the observed luminosity or
polarisation of the eclipsed star. This is related to the
underlying function through
|  |
(4) |
where  is the vector between the centres of the star and its
occultor, and the kernel
is the vector between the centres of the star and its
occultor, and the kernel  can be calculated a priori.
The set of observations that we make,
can be calculated a priori.
The set of observations that we make,  ,is therefore related to this underlying function by
,is therefore related to this underlying function by
|  |
(5) |
where  and ni is a random admixture of
noise. From these measurements we wish to
produce an estimator
and ni is a random admixture of
noise. From these measurements we wish to
produce an estimator  of the underlying function u(r).
of the underlying function u(r).
For the Backus-Gilbert method, we suppose that the mean of the
estimator and the underlying function are related by an
averaging kernel  , through
, through
|  |
(6) |
Since we do not know the underlying function, the averaging kernel is
of no use to us directly; however we can study its properties, and use
our data fi in such a way as to optimise those properties, and so
minimise the dependence of the estimate  on the underlying
function and the noise. It is clear from Eq. (6) that
on the underlying
function and the noise. It is clear from Eq. (6) that  if
if  is the Dirac delta function.
However, such a solution is highly sensitive to noise in the data and
hence very unstable. We attain stability by increasing the width of
is the Dirac delta function.
However, such a solution is highly sensitive to noise in the data and
hence very unstable. We attain stability by increasing the width of
 , and hence smoothing the recovered value over a
wider region of the source - that is, we minimise the width of
, and hence smoothing the recovered value over a
wider region of the source - that is, we minimise the width of
 subject to the conflicting demand that the
resolution of
subject to the conflicting demand that the
resolution of  is sufficient for the problem at
hand, in a sense we shall make more precise below.
is sufficient for the problem at
hand, in a sense we shall make more precise below.
We relate our data fi to our estimator  through a set of
response kernels qi(r), which produce an estimate of the
underlying function through
through a set of
response kernels qi(r), which produce an estimate of the
underlying function through
|  |
(7) |
If we substitute Eq. (5) into Eq. (7), and assume
 , then we can compare with
Eq. (6), and obtain
, then we can compare with
Eq. (6), and obtain
|  |
(8) |
This allows us to form some measure
of the width of  such as
such as
|  |
(9) |
| |
| |
which depends on qi, and depends on Ki through the definition
| 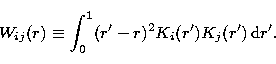 |
(10) |
This is the standard definition of the width;
others are reasonable, and may be preferable in different
circumstances.
Again assuming that 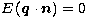 , we can also form a
measure of the stability of Eq. (7)
, we can also form a
measure of the stability of Eq. (7)
|  |
(11) |
which depends on qi and the noise covariance matrix
 . In our simulations below, we
take the ni to be independent and Gaussian with standard
deviation
. In our simulations below, we
take the ni to be independent and Gaussian with standard
deviation  ; in this case,
; in this case,  , and
our assumption
, and
our assumption 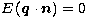 is true.
is true.
Finally, the demand that  in Eq. (6) have
unit area, leads to the constraint
in Eq. (6) have
unit area, leads to the constraint
|  |
(12) |
where  .
.
The Backus-Gilbert method consists of finding those qi(r) which
minimise
for some selected parameter  , subject to the constraint
, subject to the constraint
 . The minimisation problem has
explicit analytic solutions
. The minimisation problem has
explicit analytic solutions
| ![\begin{displaymath}
{\vec q}_\lambda(r) =
\frac{[{\vec W}(r) + \lambda {\vec ...
...cdot[{\vec W}(r) + \lambda {\vec S}]^{-1}\cdot{\vec R}}
\relax \end{displaymath}](/articles/aas/full/1998/13/ds6149/img40.gif) |
(13) |
in terms of the
parameter  , and these different solutions, when combined with the
data fi using Eq. (7), give different estimators
, and these different solutions, when combined with the
data fi using Eq. (7), give different estimators  . The nature of the trade-off in the minimisation is
clear: in order to improve the stability of the recovery, we choose a
. The nature of the trade-off in the minimisation is
clear: in order to improve the stability of the recovery, we choose a
 which makes
which makes  broader, and so generate
response kernels qi which extend the weighted average over a greater
number of the data points fi. The cost of this is that the
estimate of the recovered point will be biased by the inclusion of the
extra data, and this will be more marked when the underlying function
is rapidly varying.
broader, and so generate
response kernels qi which extend the weighted average over a greater
number of the data points fi. The cost of this is that the
estimate of the recovered point will be biased by the inclusion of the
extra data, and this will be more marked when the underlying function
is rapidly varying.
The first important point about the Backus-Gilbert method is that the
parameter  allows us to adjudicate between the conflicting
demands of minimising the width of the kernel
allows us to adjudicate between the conflicting
demands of minimising the width of the kernel  and
minimising the sensitivity of the recovered value (which is a
realisation of the statistical variable
and
minimising the sensitivity of the recovered value (which is a
realisation of the statistical variable  ) to the
measurement noise, and that this adjudication can be done prior
to any data being collected , based only on the characteristics of the
kernel
) to the
measurement noise, and that this adjudication can be done prior
to any data being collected , based only on the characteristics of the
kernel  and the noise.
and the noise.
Secondly, we must emphasise that the  we obtain
gives us, through Eq. (7), a single point in the recovered
function,
we obtain
gives us, through Eq. (7), a single point in the recovered
function,  . This means that in this simplest
version of the Backus-Gilbert method we must perform the inversion for
each value of r for which we wish to find
. This means that in this simplest
version of the Backus-Gilbert method we must perform the inversion for
each value of r for which we wish to find  .Since the calculation of the coefficients
.Since the calculation of the coefficients  involves
a matrix inversion, which is an n3 procedure, it can be
computationally expensive, but this limitation is acceptable in our
particular case, as we only wish to recover the polarisations at the
limb, r=1. This feature has the compensation that we can if
necessary select a different optimal value of
involves
a matrix inversion, which is an n3 procedure, it can be
computationally expensive, but this limitation is acceptable in our
particular case, as we only wish to recover the polarisations at the
limb, r=1. This feature has the compensation that we can if
necessary select a different optimal value of  for each
recovered point.
for each
recovered point.


Up: Inversion of polarimetric data
Copyright The European Southern Observatory (ESO)
![]() , which might be the observed luminosity or
polarisation of the eclipsed star. This is related to the
underlying function through
, which might be the observed luminosity or
polarisation of the eclipsed star. This is related to the
underlying function through


![]() , through
, through

![]() through a set of
response kernels qi(r), which produce an estimate of the
underlying function through
through a set of
response kernels qi(r), which produce an estimate of the
underlying function through



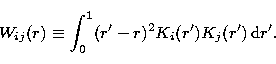
![]() , we can also form a
measure of the stability of Eq. (7)
, we can also form a
measure of the stability of Eq. (7)
![]() in Eq. (6) have
unit area, leads to the constraint
in Eq. (6) have
unit area, leads to the constraint

![\begin{displaymath}
{\vec q}_\lambda(r) =
\frac{[{\vec W}(r) + \lambda {\vec ...
...cdot[{\vec W}(r) + \lambda {\vec S}]^{-1}\cdot{\vec R}}
\relax \end{displaymath}](/articles/aas/full/1998/13/ds6149/img40.gif)
![]() allows us to adjudicate between the conflicting
demands of minimising the width of the kernel
allows us to adjudicate between the conflicting
demands of minimising the width of the kernel ![]() and
minimising the sensitivity of the recovered value (which is a
realisation of the statistical variable
and
minimising the sensitivity of the recovered value (which is a
realisation of the statistical variable ![]() ) to the
measurement noise, and that this adjudication can be done prior
to any data being collected , based only on the characteristics of the
kernel
) to the
measurement noise, and that this adjudication can be done prior
to any data being collected , based only on the characteristics of the
kernel ![]() and the noise.
and the noise.
![]() we obtain
gives us, through Eq. (7), a single point in the recovered
function,
we obtain
gives us, through Eq. (7), a single point in the recovered
function, ![]() . This means that in this simplest
version of the Backus-Gilbert method we must perform the inversion for
each value of r for which we wish to find
. This means that in this simplest
version of the Backus-Gilbert method we must perform the inversion for
each value of r for which we wish to find ![]() .Since the calculation of the coefficients
.Since the calculation of the coefficients ![]() involves
a matrix inversion, which is an n3 procedure, it can be
computationally expensive, but this limitation is acceptable in our
particular case, as we only wish to recover the polarisations at the
limb, r=1. This feature has the compensation that we can if
necessary select a different optimal value of
involves
a matrix inversion, which is an n3 procedure, it can be
computationally expensive, but this limitation is acceptable in our
particular case, as we only wish to recover the polarisations at the
limb, r=1. This feature has the compensation that we can if
necessary select a different optimal value of ![]() for each
recovered point.
for each
recovered point.