In this work, we present atomic data on Co II, i.e. calculated log(gf) values of the ultraviolet transitions. Stellar spectra in the ultraviolet region show a wealth of lines from second spectra of transition elements: Fe-group, Pd-group and Pt-group elements occur predominantly in their "singly ionized" stage in the stellar atmospheres (specifically the photospheres) of B- to G-type stars. Moreover, the class of chemically peculiar (CP) stars is known to display enhanced abundances for these heavy elements, in serious deviation from the solar abundance pattern. Being an odd-Z element, cobalt is not as abundant as chromium, iron or nickel; on the other hand, its appearance in specific astrophysical objects like Co-stars and supernovae certainly makes a study worthwhile.
The present work is part of a series of transition probability calculations in the Fe-group transition elements using orthogonal operators (Raassen & Uylings 1997; Uylings & Raassen 1997). Computational details of the method can be found in the above references.
The spectrum of Co II has been recorded using the Imperial College Fourier transform spectrometer (Thorne et al. 1987), which is operational down to 1400 Å. Experimental details and results will be published in another paper (Pickering et al. 1997).
With its appreciable nuclear dipole moment, 59Co (similar to 55Mn in the Fe-group) displays a sizeable hyperfine structure. To some degree, this has already been studied in Co I (Dembczynski et al. 1993; Dembczynski 1996; Pickering 1996). As it obviously affects abundance determinations (the line profiles will appear "too broad", Biémont 1978), we plan to give A and B hyperfine structure constants in the near future; this work will include both the FTS obtained experimental values as the calculated eigenvector composition.
Stellar iron, nickel and cobalt are products of nuclear burning in a
supernova event. Strong absorption lines can be found in supernovae of
types Ia and II (Jaschek & Jaschek 1995) as a result of
explosive nucleosynthesis. The strong Co II emission in late-type SN II may
at early epochs be due to radioactive 56Co which is, like 26Fe, a
beta-decay product of 56Ni (Rank et al. 1998); at
later times, 57Co and the stable isotope 59Co become more
important. Especially the supernova SN 1987 A has been studied in this
respect. Transition probabilities of forbidden lines in the infra-red (like
the features at 10.52 ![]() m, 1.547
m, 1.547 ![]() m and 18.8
m and 18.8 ![]() m) have been
calculated (Nussbaumer & Storey 1988) and observed
(Jennings et al. 1993), but many M1 and E2 transitions
are uncertain though needed (Li et al. 1993).
m) have been
calculated (Nussbaumer & Storey 1988) and observed
(Jennings et al. 1993), but many M1 and E2 transitions
are uncertain though needed (Li et al. 1993).
Absorption resonance lines of Co II are seen in the Interstellar Medium (ISM). The advantage of Co II (compared to Fe II e.g.) is that its lines are weaker which is more apt for ISM studies of abundances and depletions.
Widths of Co II lines have apparently been used to determine the
chromospheric turbulent velocity of the supergiant ![]() Orionis (M2 Iab)
(Carpenter & Robinson 1997).
Orionis (M2 Iab)
(Carpenter & Robinson 1997).
Orthogonal operators (Hansen et al. 1988), have the marked advantage that the parameters are stabilized in the fit. As a result, several smaller (higher order or relativistic) effects can meaningfully be added to raise the accuracy of both eigenvalues and eigenvectors.
First, the angular coefficients of the transition matrix in pure LS coupling
are found from straightforward Racah algebra. They are multiplied with the
transition integrals (given in Table 1) obtained
from a relativistic Hartree-Fock program (MCDF from Parpia et al.
1996) and corrected for core polarization (Hameed
1972; Laughlin 1992). The result of core polarization
is a decrease of ![]() of the absolute values of the transition integrals
from Parpia et al.
of the absolute values of the transition integrals
from Parpia et al.
Second, the pure but unphysical LS transition matrix is transformed into the actual intermediate coupling by the eigenvectors obtained from the orthogonal operator approach. The squared matrix elements of this final transition matrix yield the line strengths and thereby the log(gf) or the A-values.
For details on the method and parameter values, we refer to our overview article on dN-1p configurations (Uylings & Raassen 1996). Those interested in orthogonal operators are invited to contact the authors or to visit our Internet address ftp://nucleus.phys.uva.nl in the directory pub/orth.
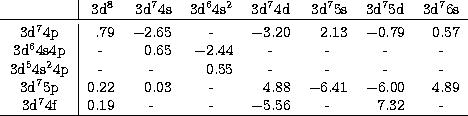 |
Copyright The European Southern Observatory (ESO)