JCJ92 suggested that the
differences found between their models and DTT89's data could be due to the
different abundance scale - we must remind that grid I scales the abundances
with [Ca/H] since grid II does with [Fe/H] - In the present models, a solar
abundance ratio
[Ca/Fe] has been assumed, but this could not be the case. In fact, both
observations and chemical evolution models show that for low abundances
([Fe/H] ![]() ) the
) the ![]() elements are enhanced with
respect to the solar partition. In particular, the behaviour of [Ca/Fe]
versus [Fe/H] is shown in Fig. 5c from
Mollá & Ferrini (1995)
for the galactic bulge: [Ca/Fe] keeps constant
(
elements are enhanced with
respect to the solar partition. In particular, the behaviour of [Ca/Fe]
versus [Fe/H] is shown in Fig. 5c from
Mollá & Ferrini (1995)
for the galactic bulge: [Ca/Fe] keeps constant
(![]() 0.5) for a low [Fe/H] abundance and thereafter it decreases
towards the solar value.
0.5) for a low [Fe/H] abundance and thereafter it decreases
towards the solar value.
The observed enhancement of alpha-elements is due to a lower
proportion of iron group elements to alpha-elements at low Z when compared
with the corresponding ratio at the solar Z value. In other words,
stars of low Z (where Z is representative of alpha-elements) have a lower
value of Fe/H than stars with higher Z, as clearly demonstrated by the
study of globular clusters. In particular stars with subsolar Z have
supersolar abundance ratios. To account for this in the comparison
between the observational and predicted values of CaT, we should use
stars of lower observed Z than the value of Z used in the theoretical
isochrones. At lower
metallicities, this effect is larger. We also performed
several tests aimed to clarify the role of the [![]() /Fe] on the
evolution of the star in the HR diagram and they confirmed that isochrones with
the same global metallicity Z but a different enhancement of the
/Fe] on the
evolution of the star in the HR diagram and they confirmed that isochrones with
the same global metallicity Z but a different enhancement of the
![]() elements are almost indistinguishable in the HR diagram (see also
Salaris et al. 1993). In summary, to compare both grids, we should
use a non solar partition of the heavy elements for abundances lower
than solar. The net effect would be a correction in the values of [Fe/H] adopted
in Eq. (7).
elements are almost indistinguishable in the HR diagram (see also
Salaris et al. 1993). In summary, to compare both grids, we should
use a non solar partition of the heavy elements for abundances lower
than solar. The net effect would be a correction in the values of [Fe/H] adopted
in Eq. (7).
The real effect of different [Ca/Fe] ratios has been taken into account by Idiart et al. (1997). These authors, by measuring the CaT index in a sample of stars whose [Ca/H] and [Fe/H] were known, found a weak dependence of CaT index with the [Ca/Fe] ratio.
In the galactic star sample used by DTT89 this effect only appears at low metallicity. Therefore it explains the differences between DTT89 and JCJ92 results found in panels c) and d), because the low abundance stars present in DTT89s sample have been used to compute our grid II. However, the same explanation cannot be invoke in the case of solar abundance, panel b), where the partition must be solar for the neighbourhood stars.
The differences found between the two grids in the
oldest populations at Z = 0.008 could be due to the use, in grid II, of the
solar M-late relation, Eq. (11), also at Z=0.008, producing values
of EW(CaT) that could be overestimated. This does not occur in grid I, in
which both ![]() and abundance dependence are consistently
taken into account in the theoretical calibrations. For these reasons we
consider grid I more reliable than grid II although, on the other hand, this
last one rest on the extrapolation of the JCJ's relation for the coolest stars,
for which unfortunately, we have not found observed values either theoretical
models.
and abundance dependence are consistently
taken into account in the theoretical calibrations. For these reasons we
consider grid I more reliable than grid II although, on the other hand, this
last one rest on the extrapolation of the JCJ's relation for the coolest stars,
for which unfortunately, we have not found observed values either theoretical
models.
The above disagreement between the two grids notwithstanding, we may draw the following general conclusions.
At the higher metallicities the EW(CaT) shows a clear maximum around 10 Myr. This is due to the prominence of the RSG phase at these ages and metal content. At earlier stages massive stars evolve according to the O-BSG-WR sequence, while at lower metallicity the scheme followed is O-BSG-YSG-RSG, with the later phase being only a tiny fraction of the total lifetime.
The dependence on metallicity can be easily quantified. Synthetic values of
the index higher than 7 Å are only found in models with metallicity
![]() or higher, reaching values as high as 11 Å only for 2.5
or higher, reaching values as high as 11 Å only for 2.5 ![]() models. The variation with the metallicity is due, on one hand, to the
intrinsic dependence of the index and, on the other, to the stellar
evolution effect just described (see also Sect. 2.1)
models. The variation with the metallicity is due, on one hand, to the
intrinsic dependence of the index and, on the other, to the stellar
evolution effect just described (see also Sect. 2.1)
From this maximum value the index decreases as the age increases up to a value of about 100 Myr. In the case of the two metal poor sets the index remains almost constant with time up to this age. Around 100 Myr the appearance of the AGB phase produces a sudden increase of the index which then decreases until 1 Gyr. At this stage the advent of the RGB induces another discontinuity which is more evident at the highest metallicity. As the increasing duration of the RGB phase at increasing age is compensated by a decrease of the evolutionary flux of stars and by a shortening of the AGB phase, the integrated value of the index becomes almost age-independent. In clusters older than a few Gyr the metallicity is the dominant parameter driving the integrated value of EW(CaT).
![\begin{figure}
\begin{center}
\includegraphics [width=5.9cm,height=8.8cm,angle=-90]{vargas5.eps}
\end{center}\end{figure}](/articles/aas/full/1998/12/ds1379/Timg43.gif) |
Figure 5: EW(CaT) versus [Fe/H]. Filled symbols are data measured in old galactic globular clusters compiled from the literature (Bica & Alloin 1986b, 1987; Armandroff & Da Costa 1991; Armandroff et al. 1992 and Geisler et al. 1995). Open symbols are our two grids of models as labelled in the plot |
It would be desirable to compare these models with the equivalent widths of clusters at different ages and metallicities (SSP) making use of the same isochrones library.
The main body of available data is the one from Bica & Alloin (1986a,b) who presented a data-base of star clusters at different ages and metallicities. For the young metal-poor clusters in the Magellanic Clouds, Bica et al. (1986, 1990) give also the value of the CaT, but the error bars quoted for the age and metallicity are too large to provide a reliable test for our models.
In the case of old SSPs, for which we have shown that the CaT index is
mainly a function of abundance, we have collected in Fig. 5 the observed
values of the EW(CaT) against [Fe/H] for several globular clusters and
we have compared them with the results from our models at an age of 13 Gyr. We
must refer our results to [Fe/H] abundance scale. This is the case of grid II.
However, since grid I uses [Ca/H], we must account for the enhacement of
[![]() -elements/Fe] as we have explained above. Therefore, we have assigned
the value of [Fe/H] for every total abundance Z or [Ca/H] value,
by using the [Ca/Fe] relation found by
Mollá & Ferrini (1995) already quoted.
This relation implies a correction of 0.0, -0.2 and -0.4 dex for values of
[Ca/H] solar, 0.4 solar and 0.2 solar respectively.
-elements/Fe] as we have explained above. Therefore, we have assigned
the value of [Fe/H] for every total abundance Z or [Ca/H] value,
by using the [Ca/Fe] relation found by
Mollá & Ferrini (1995) already quoted.
This relation implies a correction of 0.0, -0.2 and -0.4 dex for values of
[Ca/H] solar, 0.4 solar and 0.2 solar respectively.
Data in Fig. 5 shows that in old systems a narrow correlation between the CaT index and the metallicity over more than two orders of magnitude in [Fe/H] is found and, at the same time, they provide a significant reliability test for the theoretical models presented here.
Finally, a recent paper by
Mayya (1997) presents CaT synthesis models to be
applied to starburst regions. Therefore only young population results
may be compared with our models. Mayya uses JCJ92 fitting functions for
![]() and DTT89 empirical relations for higher metallicities. He uses the
stellar evolutionary tracks from Geneva group. His results also show a primary
peak due to the RSG phase, a secondary maximum and a low constant value for
SSP older than 100 Myr. Both peaks occur at earlier ages than in our
models, due to differences in the assumed stellar tracks, and the
asymptotic value is lower than the one in our grid II. The
most important difference appears at lower abundances: at Z=0.008 the
first maximum disappears in our models, while it exists in Mayya's. The
evolutionary tracks selected by
Mayya (1997) with enhaced mass loss rates for low
abundances produce this behaviour, not predicted with the Padova evolutionary
models either previous generation of Geneve tracks. The convenience of the use
of these enhanced mass loss rates is still a matter of debate.
and DTT89 empirical relations for higher metallicities. He uses the
stellar evolutionary tracks from Geneva group. His results also show a primary
peak due to the RSG phase, a secondary maximum and a low constant value for
SSP older than 100 Myr. Both peaks occur at earlier ages than in our
models, due to differences in the assumed stellar tracks, and the
asymptotic value is lower than the one in our grid II. The
most important difference appears at lower abundances: at Z=0.008 the
first maximum disappears in our models, while it exists in Mayya's. The
evolutionary tracks selected by
Mayya (1997) with enhaced mass loss rates for low
abundances produce this behaviour, not predicted with the Padova evolutionary
models either previous generation of Geneve tracks. The convenience of the use
of these enhanced mass loss rates is still a matter of debate.
CaT has been observed not only in star clusters and normal galaxies but also in Active Galaxies (Terlevich et al. 1990a; Nelson & Whittle 1995; Palacios et al. 1997) and star-forming regions like Starbursts (Terlevich et al. 1990a,b; García-Vargas et al. 1993; González-Delgado et al. 1995) and Giant Extragalactic HII Regions, GEHRs, (Pastoriza et al. 1993; González-Delgado et al. 1995; Terlevich et al. 1996).
There is a controversy related to the origin of the observed CaT in star-forming regions and AGNmostly because these regions are not spatially resolved from the ground. Therefore one of the key questions is if the observed CaT comes from a single stellar population RSG rich or from a result of a mixture of populations of varying age and possibly metallicity (including the RSG plus the underlying older population).
In the case of isolated GEHRs, and therefore not contaminated by an underlying old population, two possibilities can arise: (1) the production of the CaT is due to the same young burst that is ionizing the region and (2) the CaT is produced in a slightly older (10-15 Myr) population, coexisting in the same GEHR with the younger, ionizing, one. With respect to the first scenario, current theoretical models (Salasnich et al. 1997) predict a narrow range of age and metallicity in which an SSP can produce both ionizing stars (O and WR stars) and RSG, namely around 4-6 Myr and at solar metallicity. This has been proposed for the CaT observations in NGC 604 (Terlevich et al. 1996). However, some other GEHR need the existence of an older component, second scenario, such is the case of some GEHR in the circumnuclear region of NGC 7714 (García-Vargas et al. 1997).
The largest circumnuclear GEHRs usually show the CaT feature in their spectra. However, some contamination from the older underlying population in the host galaxy is expected and therefore it is not clear whether the CaT is originated in the GEHR or in the disk-bulge population (García-Vargas et al. 1997).
In the case of starburst galaxies and AGN the picture is even more
difficult to interpret, and the need for models which include the CaT
synthesis from different populations becomes a key issue. To study this
problem we have computed composite models with a combination of
three different kind of populations: (a) a young one, able to ionize the
gas, and definitively present in the region, (b) an intermediate age one,
RSG rich, and (c) a very old population representative of those
present in ellipticals and bulges of spirals. The selected ages are, 2.5
and 5 Myr for the youngest population, 8 and 12 Myr for the intermediate
component and 10 Gyr for the oldest one. Three types of models have
been computed: (1) a combination of two coexisting bursts, young, and
intermediate, contributing 50% each in mass, suitable to be used in
GEHRs, without any underlying population; (2) a two-component
model in which the young burst plus the old population are combined in different
proportions, and (3) a three-component model in which two coexisting bursts,
young and intermediate-age, plus the old underlying population are contributing
to the light in different percentages. The metallicity of the old population has
been
chosen to be ![]() , 0.4
, 0.4 ![]() and 0.2
and 0.2 ![]() for young populations with
2.5
for young populations with
2.5 ![]() ,
, ![]() and 0.4
and 0.4 ![]() respectively, according to what is predicted by
chemical evolution models.
respectively, according to what is predicted by
chemical evolution models.
To define the relative proportions we use the ratio, P, of the continuum
luminosity at 6500 Å (close to ![]() ) of the young and intermediate
population (when present) to the total light. As an example P =
0.10 indicates a model in which the population characteristic of the region
(young or young + intermediate) is contributing 10% to the total light
in the continuum at
) of the young and intermediate
population (when present) to the total light. As an example P =
0.10 indicates a model in which the population characteristic of the region
(young or young + intermediate) is contributing 10% to the total light
in the continuum at ![]() . This method allows a check of the adopted
proportions by a direct inspection of the
. This method allows a check of the adopted
proportions by a direct inspection of the ![]() images. We have computed models
with P ranging from the ones typical of GEHRs (P = 0.10 - 1 going from the
smallest
to the largest regions) to the ones characteristic of the most powerful
starburst galaxies (P= 1 - 100).
images. We have computed models
with P ranging from the ones typical of GEHRs (P = 0.10 - 1 going from the
smallest
to the largest regions) to the ones characteristic of the most powerful
starburst galaxies (P= 1 - 100).
Tables 7, 8 (grid I) 9 and 10 (grid II) display the results of
the composite-population models. Each table contains the results for
three metallicities: 0.4 ![]() ,
, ![]() and 2.5
and 2.5 ![]() . The first column lists
the proportion, P, defined above (including the two - Tables 7, 9 -- or
three -- Tables 8, 10 -- populations considered). If P is not given, a
single population, or a combination of two coexisting young populations
contributing 50% in mass each, have been considered. Column 2 shows the age
of the population(s), in Myr. Therefore 2.5 + 104 correspond to a model in
which a young burst of 2.5 Myr is combined with an old population of 10 Gyr.
Column 3, EW(CaT), lists the value of the equivalent width of CaT in
absorption, in Å, for each model. Finally Col. 4 is the equivalent width of
. The first column lists
the proportion, P, defined above (including the two - Tables 7, 9 -- or
three -- Tables 8, 10 -- populations considered). If P is not given, a
single population, or a combination of two coexisting young populations
contributing 50% in mass each, have been considered. Column 2 shows the age
of the population(s), in Myr. Therefore 2.5 + 104 correspond to a model in
which a young burst of 2.5 Myr is combined with an old population of 10 Gyr.
Column 3, EW(CaT), lists the value of the equivalent width of CaT in
absorption, in Å, for each model. Finally Col. 4 is the equivalent width of
![]() Balmer line in emission. If this value is missing then the adopted
population(s) is(are) too old to produce ionizing photons.
Balmer line in emission. If this value is missing then the adopted
population(s) is(are) too old to produce ionizing photons.
The predicted values of EW(![]() ) in emission have been computed without
considering the dust associated to the ionized region. There exists a well
known discrepancy between predicted and observed values of EW(H
) in emission have been computed without
considering the dust associated to the ionized region. There exists a well
known discrepancy between predicted and observed values of EW(H![]() )(e.g. Viallefond & Goss 1986). In fact, only 3 out of 425 HII galaxies in
the catalogue by Terlevich et al. (1991) show EW(H
)(e.g. Viallefond & Goss 1986). In fact, only 3 out of 425 HII galaxies in
the catalogue by Terlevich et al. (1991) show EW(H![]() ) comparable
to the ones calculated for clusters younger than about 3 Myr (i.e. > 350
Å; Mas-Hesse & Kunth 1991;
García-Vargas et al. 1995a;
Stasinska & Leitherer 1996).
Under the assumption of a single burst
population and a radiation bound nebula, an explanation for this
disagreement could be that the reddening affecting the emission lines is
caused by dust inside the regions (associated to the gas) which therefore
does not affect the continuum of the ionizing cluster
(Mayya & Prabhu 1996). If this is the case, the measured EW(H
) comparable
to the ones calculated for clusters younger than about 3 Myr (i.e. > 350
Å; Mas-Hesse & Kunth 1991;
García-Vargas et al. 1995a;
Stasinska & Leitherer 1996).
Under the assumption of a single burst
population and a radiation bound nebula, an explanation for this
disagreement could be that the reddening affecting the emission lines is
caused by dust inside the regions (associated to the gas) which therefore
does not affect the continuum of the ionizing cluster
(Mayya & Prabhu 1996). If this is the case, the measured EW(H![]() ) should be
increased according to the reddening determined from the emission lines and
taking into account the contribution of the nebular continuum
(García-Vargas et al. 1997).
) should be
increased according to the reddening determined from the emission lines and
taking into account the contribution of the nebular continuum
(García-Vargas et al. 1997).
Columns 5, 6 ( ![]() ) and 7, 8 (0.4
) and 7, 8 (0.4 ![]() ) contain
the same as Cols. 3, 4 already described for the case of 2.5
) contain
the same as Cols. 3, 4 already described for the case of 2.5 ![]() .
.
To summarize the results, we plot in Fig. 6 the value of EW(CaT) against
that of EW(H![]() ). This figure can be used as a diagnostic diagram
to unveil the presence of an intermediate population RSG rich,
when analyzing data of star-forming regions which are located over
an older underlying population. This is usually the case of AGN, nuclear
starbursts and circumnuclear GEHRs. The results for the grid I are divided in
in four panels.
These panels simulate four different types of star-forming regions: a) AGN,
corresponding to solar metallicity and large P values, b) circumnuclear high
metallicity HII regions with solar metallicity but low P values, c) nuclear
starbursts having half solar metallicity and high
P, and d) circumnuclear GEHR with moderate metallicity (0.4
). This figure can be used as a diagnostic diagram
to unveil the presence of an intermediate population RSG rich,
when analyzing data of star-forming regions which are located over
an older underlying population. This is usually the case of AGN, nuclear
starbursts and circumnuclear GEHRs. The results for the grid I are divided in
in four panels.
These panels simulate four different types of star-forming regions: a) AGN,
corresponding to solar metallicity and large P values, b) circumnuclear high
metallicity HII regions with solar metallicity but low P values, c) nuclear
starbursts having half solar metallicity and high
P, and d) circumnuclear GEHR with moderate metallicity (0.4 ![]() ) and low
P values.
) and low
P values.
Inspection of Tables 7, 8 and Fig. 6 shows that for powerful starburst galaxies (with values of P larger than 1.00) values of EW(CaT) higher than 3.8 Å are predicted only if RSG are present in the region and, in this case, the two-component models (ionizing burst+bulge) would not be able to reproduce the observations. García-Vargas et al. (1993) gave values of CaT in starbursts ranging between 2.5 and 8 Å. As can be seen in Fig. 6c a value as low as 2.5 Å can imply a low metallicity, an older age or simply the absence of RSG, and only a detailed study of other observational constraints could provide the solution. On the contrary, values as high as 8 Å would necessarily imply the presence of RSG and a metallicity at least solar, therefore somewhat higher than the average metallicity found in starburst galaxies.
The same method can be applied to AGN. In this case, a detection of CaT
higher than 5 Å implies the presence of RSG inside the region sampled by
the slit, probably larger than the nucleus and including also the subarcsec
circumnuclear rings as shown by HST observations of some of the nearest
AGN
(Colina et al. 1997).
Terlevich et al. (1990a) showed that all AGN in
their sample had values of EW(CaT) ![]() 5 Å, therefore implying the
presence of RSG.
5 Å, therefore implying the
presence of RSG.
In the case of circumnuclear GEHRs the discrimination between the presence
or absence of RSG is a difficult task, particularly at moderate
metallicity (see Figs. 6b and 6d). A more detailed study with further
observational constraints is needed to discriminate between the two
possibilities, such as the analysis of the whole optical spectrum to
constrain the age of the young burst and an image near ![]() to determine P
(García-Vargas et al. 1997)
to determine P
(García-Vargas et al. 1997)
We now turn to old populations, namely elliptical galaxies and bulges of
spirals. Terlevich et al. (1990a) present a sample of 14 objects, whose
EW(CaT) are between 6.1 and 8.1 Å (typical error bar of ![]() 0.8 Å)
measured as in DTT89 and thus directly comparable to our models.
Delisle & Hardy (1992) give central values (and also
gradients) for 12 galaxies, with CaT equivalent widths
ranging between 6.4 and 7.7 Å (typical error bar of
0.8 Å)
measured as in DTT89 and thus directly comparable to our models.
Delisle & Hardy (1992) give central values (and also
gradients) for 12 galaxies, with CaT equivalent widths
ranging between 6.4 and 7.7 Å (typical error bar of ![]() 0.2 Å). In
spite of different spectral band-passes than DTT89, but also free from
TiO bands contamination, the comparison of three common objects, M 31,
M 81 and NGC 1700, gives values of 6.4, 7.3 and 7.0 Å in
Delisle &
Hardy (1992) and 6.1, 7.7 and 6.1 in
Terlevich et al. (1990a) respectively,
which are consistent within the errors. In summary the available observed
values of the CaT index in old populations (elliptical and bulges of spirals)
are between 6 and 8 Å. These numbers compare well with our old SSP
models of solar metallicity (Fig. 4b) and suggest a quite uniform average
metallicity for these systems in agreement with what is derived by detailed
galactic models of narrow band indices
(Bressan et al. 1996).
0.2 Å). In
spite of different spectral band-passes than DTT89, but also free from
TiO bands contamination, the comparison of three common objects, M 31,
M 81 and NGC 1700, gives values of 6.4, 7.3 and 7.0 Å in
Delisle &
Hardy (1992) and 6.1, 7.7 and 6.1 in
Terlevich et al. (1990a) respectively,
which are consistent within the errors. In summary the available observed
values of the CaT index in old populations (elliptical and bulges of spirals)
are between 6 and 8 Å. These numbers compare well with our old SSP
models of solar metallicity (Fig. 4b) and suggest a quite uniform average
metallicity for these systems in agreement with what is derived by detailed
galactic models of narrow band indices
(Bressan et al. 1996).
Vazdekis et al. (1996, V96) compute evolutionary synthesis
models for early-type galaxies, with metallicities 0.4 ![]() ,
, ![]() , and
2.5
, and
2.5 ![]() and ages 1, 4, 8, 12 and 17 Gyr. They consider different hypotheses
about the IMF, the
chemical evolution and the star formation history, producing a set of
models which includes colours and line indices, in particular CaT.
Since the evolutionary scheme is the same as the one
assumed in our models, we present in Table 11 a comparison between V96
models and our grid II for the SSP with common ages and metallicities.
and ages 1, 4, 8, 12 and 17 Gyr. They consider different hypotheses
about the IMF, the
chemical evolution and the star formation history, producing a set of
models which includes colours and line indices, in particular CaT.
Since the evolutionary scheme is the same as the one
assumed in our models, we present in Table 11 a comparison between V96
models and our grid II for the SSP with common ages and metallicities.
V96 give values higher than grid II at Z=0.02 and 0.05, and lower at Z=0.008
(except at 1 Gyr). For the highest metallicity,
a source of the discrepancy could be the different assumed fitting function
for the index (although both based on DTT89, they use a single fit for any
abundance, as in DTT89, since we use Eqs. (8) and (9) for ![]() and
2.5
and
2.5 ![]() . The rest should be due to the inclusion in our models
of the coolest late-type stars, Z91, and therefore a different modelization of
CaT index for cool stars, important in old populations. This comparison stress
the
need of observations of cool stars to test the present calibrations.
. The rest should be due to the inclusion in our models
of the coolest late-type stars, Z91, and therefore a different modelization of
CaT index for cool stars, important in old populations. This comparison stress
the
need of observations of cool stars to test the present calibrations.
Idiart et al. (1997) also compute synthetic values of CaT in old populations.
They use a calibration based on their own star sample, with a different index
definition, which includes the three calcium lines. They also include in their
models late-type stars from Z91 but not high metallicity RSG stars (although
these stars are not present in such old populations, the lack of high
metallicity RSG in their star sample implies that their values would be
definitively lower than ours in RSG-rich populations at metallicities solar or
higher than solar). In the range-age (1-12 Gyr) in which we can compare our
models with Idiart's, their resulting EW(CaT) for SSP are slightly lower than
those from our grid II models. However, the values agree quite well (as an
example, at 0.3 ![]() their values are 5.53 and 6.50 Å for populations at 1
Gyr and 12 Gyr, since ours (as calculated as an average value of 0.2 and 0.4
their values are 5.53 and 6.50 Å for populations at 1
Gyr and 12 Gyr, since ours (as calculated as an average value of 0.2 and 0.4
![]() ) are 5.69 and 7.19 Å respectively. At
) are 5.69 and 7.19 Å respectively. At ![]() Idiart's values are 6.57
and 7.55 Å again for the extreme ages 1 Gyr and 12 Gyr, since ours are 6.84
and 8.60 Å at the same ages. Differences can come not only from the
calculations in the CaT index but from the different assumptions adopted in the
low-mass limit of the IMF and in the evolution of the low-mass stars.
Idiart's values are 6.57
and 7.55 Å again for the extreme ages 1 Gyr and 12 Gyr, since ours are 6.84
and 8.60 Å at the same ages. Differences can come not only from the
calculations in the CaT index but from the different assumptions adopted in the
low-mass limit of the IMF and in the evolution of the low-mass stars.
An important point is the relatively low sensitivity of the
CaT index to the age above a few Gyr, makes it a very powerful tool for
discriminating among the metallicity of the stellar systems.
It is well known that due to the similar response of the isochrone turn-off
to variations in age or metallicity it is difficult to disentangle age and
metallicity effects by the sole analysis of the integrated properties of
the spectra in old populations. Different diagnostic diagrams have been
adopted, as can be seen in González (1993)
and Bressan et al. (1996)
none of which is fully adequate to overcome this difficulty.
The quantity
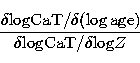 |
(12) |
![\begin{figure}
\begin{center}
\includegraphics [width=5.9cm,height=8.8cm,angle=-90]{vargas7.eps}
\end{center}\end{figure}](/articles/aas/full/1998/12/ds1379/Timg56.gif) |
Figure 7:
EW(CaT) (grid I, this work) versus the computed values for the
logarithm of
|
Figure 7 shows the synthetic values of the EW(CaT) plotted
against the logarithm of ![]() index as modelled by
Bressan et al. (1996). It can
be
seen that curves of constant age are almost orthogonal to curves of
constant metallicity, making this diagram one of the most powerful tools to
solve the problem of the age-metallicity degeneracy in elliptical galaxies
in a similar way to Fig. 2 from
Jones & Worthey (1995).
index as modelled by
Bressan et al. (1996). It can
be
seen that curves of constant age are almost orthogonal to curves of
constant metallicity, making this diagram one of the most powerful tools to
solve the problem of the age-metallicity degeneracy in elliptical galaxies
in a similar way to Fig. 2 from
Jones & Worthey (1995).
Although more theoretical work has to be made to assess the importance of the study of CaT in old systems, the use of the later index as a straightforward metallicity indicator in early-type galaxies is very promising (Gorgas et al. 1997).
Copyright The European Southern Observatory (ESO)