

Up: Multiplicity among peculiar A stars,
Subsections
This star was classified A3-F2-F5 by Osawa (1965) and Ap Si Sr by Bertaud &
Floquet (1974). As kindly pointed by
Renson (1994, personal communication to PN), Babcock (1958)
had already
found it double-lined, but did not give any period.
Interestingly, Babcock listed this star as probably magnetic, and mentioned
the profile of the K line as peculiar; as Babel (1994) showed, cool magnetic
Ap stars have a peculiar profile of the CaII K line which betrays a
stratification of calcium in the star's atmosphere. Perhaps this star should
be indeed classified Ap after all. We secured 56 points
(see Tables 9, 10 and Fig. 7)
and obtained the orbital elements listed in Table 1.
![\begin{figure}
\includegraphics [width=8.5cm]{ds7203f7.eps}\end{figure}](/articles/aas/full/1998/11/ds7203/Timg57.gif) |
Figure 7:
Radial-velocity curve of HD 43478.
The period is 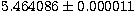 days. Notice that the zero phase
corresponds here to the quadrature (epoch given in Table 1) but not to the
primary eclipse (Eq. 3) which would fall here at phase 0.75, when the
more massive component passes in front of the less massive one days. Notice that the zero phase
corresponds here to the quadrature (epoch given in Table 1) but not to the
primary eclipse (Eq. 3) which would fall here at phase 0.75, when the
more massive component passes in front of the less massive one |
![\begin{figure*}
\centering
\includegraphics [width=16cm]{ds7203f8.eps}\end{figure*}](/articles/aas/full/1998/11/ds7203/Timg58.gif) |
Figure 8:
Lightcurves of HD 43478 for the [V]
magnitude and the [U-B] and [B-V] colour indices of Geneva photometry,
plotted according to the ephemeris given in Eq. (3).
Notice the lack of colour change during eclipses. The best fit to the [V]
curve is shown (see Table 4) |
The system is especially interesting, because we discovered eclipses, which
allow to determine the orbital inclination (North & Nicolet 1994).
Unfortunately, the eclipses are shallow, as shown if Fig. 8 where the
lightcurve is plotted according to the ephemeris:
| 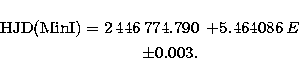 |
(3) |
| |
In addition, the number of measurements is small, due to the unfavourable
period (close to 5.5 days) and we had a relatively small number of good nights at the Jungfraujoch station on the critical dates.
The descending branch of the primary minimum was observed during a mediocre,
partial night where only five standards could be measured; nevertheless,
the scatter around the fitted lightcurve is fairly good.
The two minima have about the same depth and are separated by exactly 0.5 in
phase, confirming the circularity of the orbit. On the other hand, the [U-B]
and [B-V] curves remain flat during both eclipses, showing that both
components have similar effective
temperatures. In spite of the small number of points, we analized the lightcurve
with the EBOP16 programme (Etzel 1980, 1991). The Geneva and 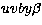 photometric indices and parameters give very consistent
photometric indices and parameters give very consistent  and
and
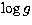 values through the calibration of Künzli et al. (1997) for the Geneva system, and through the
calibration of Moon & Dworetsky (1985) for the
values through the calibration of Künzli et al. (1997) for the Geneva system, and through the
calibration of Moon & Dworetsky (1985) for the
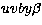 system (Table 3). For the
system (Table 3). For the 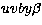 system, we applied the
correction recommended by Dworetsky & Moon (1986) to the
system, we applied the
correction recommended by Dworetsky & Moon (1986) to the 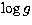 value for the Am stars.
value for the Am stars.
Table 3:
Physical parameters of HD 43478 according to its colours in the 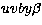 and Geneva photometric systems. Both components are assumed to be
identical. Note that
and Geneva photometric systems. Both components are assumed to be
identical. Note that 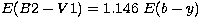 . The errors quoted for the
physical parameters determined with Geneva photometry are propagated from
typical errors on the colour indices but do not include possible systematic
errors related with the calibration itself. The reddening E(B2-V1)=0.089
corresponds to E(B-V)=0.1 suggested by the maps of Lucke (1978) and is
mentioned only to illustrate its effect on the physical parameters; the
adopted colour excess E(B2-V1)=0.045 is obtained from E(b-y) = 0.039,
which results from the calibrated
. The errors quoted for the
physical parameters determined with Geneva photometry are propagated from
typical errors on the colour indices but do not include possible systematic
errors related with the calibration itself. The reddening E(B2-V1)=0.089
corresponds to E(B-V)=0.1 suggested by the maps of Lucke (1978) and is
mentioned only to illustrate its effect on the physical parameters; the
adopted colour excess E(B2-V1)=0.045 is obtained from E(b-y) = 0.039,
which results from the calibrated 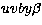 colours
colours
|
|
From the values of 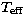 and
and 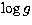 , we interpolated the linear
limb-darkening coefficient u from the tables of Van Hamme (1993).
With the
available photometric data, it is impossible to fit simultaneously all the
interesting parameters, namely the central surface brightness of the secondary
, we interpolated the linear
limb-darkening coefficient u from the tables of Van Hamme (1993).
With the
available photometric data, it is impossible to fit simultaneously all the
interesting parameters, namely the central surface brightness of the secondary
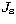 , the radius
, the radius 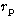 of the primary, the ratio k of the radii and the
orbital inclination i. This is a well-known difficulty for all systems
(even well detached ones) where both components are nearly identical, even when
the eclipses are deep. Another type of data has to be used to constrain the
ratio of radii, because the latter may be changed from e.g. 0.6 to 1.4,
without any change in the rms scatter of the residuals. We do not have
detailed spectroscopic informations, but the CORAVEL data allow to have a
rough guess of the k ratio in the two following ways:
of the primary, the ratio k of the radii and the
orbital inclination i. This is a well-known difficulty for all systems
(even well detached ones) where both components are nearly identical, even when
the eclipses are deep. Another type of data has to be used to constrain the
ratio of radii, because the latter may be changed from e.g. 0.6 to 1.4,
without any change in the rms scatter of the residuals. We do not have
detailed spectroscopic informations, but the CORAVEL data allow to have a
rough guess of the k ratio in the two following ways:
- 1.
- The width (FWHM) of the autocorrelation dip can be translated in terms
of
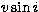 through a proper calibration (Benz & Mayor 1984).
Assuming there is no other cause
of broadening than in normal stars (i.e. no Zeeman broadening, for instance),
one obtains in this way the projected rotational velocities given in Table 2.
If synchronism has taken place between spin and orbital periods, which appears
highly probable given the rather evolved state of the system (low
through a proper calibration (Benz & Mayor 1984).
Assuming there is no other cause
of broadening than in normal stars (i.e. no Zeeman broadening, for instance),
one obtains in this way the projected rotational velocities given in Table 2.
If synchronism has taken place between spin and orbital periods, which appears
highly probable given the rather evolved state of the system (low 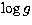 )and the circular orbit (circularisation time is longer than synchronisation
time according to tidal theories), then k is directly given by the ratio
of the
)and the circular orbit (circularisation time is longer than synchronisation
time according to tidal theories), then k is directly given by the ratio
of the 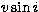 values, i.e. 0.73.
values, i.e. 0.73.
- 2.
- The equivalent width W of the autocorrelation dip depends on effective
temperature and metallicity of the star, but also on the amount of dilution
of the stellar flux by the companion's flux. Assuming that both stars have the
same effective temperature (as suggested by the flat [U-B] and [B-V] curves)
and the same metallicity (a more adventurous assumption), the ratio W2/W1
gives directly the luminosity ratio L2/L1 and is equal to the square
of the ratio of radii k2. One obtains in this way k=0.79.
A larger weight has to be granted to the first method, so we adopt here
k=0.75, keeping in mind that the uncertainty on this quantity remains
considerable (20% or so).
The final elements found with the EBOP16 programme are given in
Table 4. They are rather approximate, but the inclination is relatively well
determined and so are the masses too. It is necessary here to comment briefly
on the definition of "primary'' and "secondary'' components, because it is
not necessarily the same when radial velocities, respectively lightcurves are
considered. From the radial-velocity standpoint, the primary evidently
corresponds to the smaller amplitude K and to the more massive component.
But, when interpreting the lightcurve, the EBOP code assumes that the deeper (or
primary) eclipse corresponds to the secondary passing in front of the
primary component. In this particular system, it is interesting to notice
that the primary minimum corresponds to phase 0.75 of the 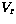 curve, where
the less massive component lies behind the primary, not the reverse.
Therefore, the adopted ratio of radii entered into the EBOP code should not be
k = r2/r1 = 0.75, but
curve, where
the less massive component lies behind the primary, not the reverse.
Therefore, the adopted ratio of radii entered into the EBOP code should not be
k = r2/r1 = 0.75, but 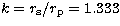 , since we have to identify the
dynamical primary (1) with the photometric secondary (s) and the dynamical
secondary (2) with the photometric primary (p). Interestingly, this implies
a larger surface brightness of the dynamical secondary than of the primary,
i.e. a slightly larger effective temperature, a relatively rare occurence.
The effective temperatures have been computed from an apparent
, since we have to identify the
dynamical primary (1) with the photometric secondary (s) and the dynamical
secondary (2) with the photometric primary (p). Interestingly, this implies
a larger surface brightness of the dynamical secondary than of the primary,
i.e. a slightly larger effective temperature, a relatively rare occurence.
The effective temperatures have been computed from an apparent
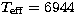 K (average of Geneva and
K (average of Geneva and  estimates) which
is assumed to result from a weighted average of the components' reciprocal
temperatures:
estimates) which
is assumed to result from a weighted average of the components' reciprocal
temperatures:
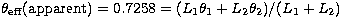 ,and assuming
,and assuming 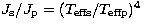 .The bolometric luminosity has been computed assuming
.The bolometric luminosity has been computed assuming 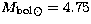 .
.
Table 4:
Parameters of HD 43478 obtained from the [V] magnitude using
the EBOP16 code and assuming the ratio of radii r2/r1 = 0.75. The indicated
errors are the formal ones only and do not include the large uncertainty
on k. Notice that the subscripts p and s refer to the photometric
primary and secondary respectively (the "secondary'' being defined as the
foreground star at Min. I) but correspond to the subscripts 2 and 1 (in this
order), which correspond to the less and more massive star respectively
|
|
Table 5:
Physical parameters of the components of HD 43478. The error on
the masses includes a large, 20% uncertainty on k, which translates into
a 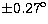 uncertainty on i. The same is true of the
radii, whose uncertainties are mutually anticorrelated since the sum of
radii remains constant within 3% as k is varied
uncertainty on i. The same is true of the
radii, whose uncertainties are mutually anticorrelated since the sum of
radii remains constant within 3% as k is varied
|
|
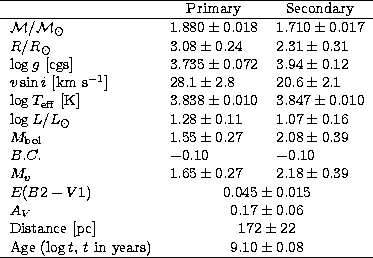
A summary of the physical parameters of the HD 43478 system is given in
Table 5. The bolometric correction has been taken from
Schmidt-Kaler (1982).
The distance is shorter than indicated by the Hipparcos satellite,
which gave 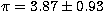 mas or d = 258-50+82 pc; however,
the discrepancy cannot be considered significant since it remains largely
within two sigmas. The distance deduced from the fundamental radii and
photometric effective temperatures is almost twice more accurate than that
given by Hipparcos (the error has been estimated using the usual propagation
formula applied to the distance modulus). It is interesting that the fundamental
mas or d = 258-50+82 pc; however,
the discrepancy cannot be considered significant since it remains largely
within two sigmas. The distance deduced from the fundamental radii and
photometric effective temperatures is almost twice more accurate than that
given by Hipparcos (the error has been estimated using the usual propagation
formula applied to the distance modulus). It is interesting that the fundamental 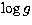 value we find for the primary, which is quite reliable, is in excellent agreement with the value obtained from both Geneva and
value we find for the primary, which is quite reliable, is in excellent agreement with the value obtained from both Geneva and 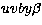 colour
indices.
colour
indices.
The situation of both components in the HR diagram is
shown in Fig. 9, together with Z=0.020 evolutionary tracks interpolated
in those of Schaller et al. (1992) and isochrones with ages 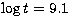 and 9.2. The primary is clearly at the end of its life on the Main Sequence,
and the secondary is probably somewhat evolved too. In view of the shape
of the isochrones, one can easily understand why the secondary is slightly
hotter than the primary. Clearly, a more complete and precise
lightcurve is needed, especially to give a more accurate, fundamental estimate
of the radii and to assess thereby the validity of the assumption of
synchronism.
and 9.2. The primary is clearly at the end of its life on the Main Sequence,
and the secondary is probably somewhat evolved too. In view of the shape
of the isochrones, one can easily understand why the secondary is slightly
hotter than the primary. Clearly, a more complete and precise
lightcurve is needed, especially to give a more accurate, fundamental estimate
of the radii and to assess thereby the validity of the assumption of
synchronism.
![\begin{figure}
\centering
\includegraphics [width=8.5cm]{ds7203f9.eps}\end{figure}](/articles/aas/full/1998/11/ds7203/Timg78.gif) |
Figure 9:
HR and 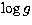 vs. vs. 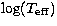 diagrams for both
components of HD 43478. The position of the primary is fairly well defined,
while that of the secondary is less reliable. The continuous lines are
the ZAMS and evolutionary tracks interpolated for the measured masses, while
the dotted and broken lines are the isochrones at diagrams for both
components of HD 43478. The position of the primary is fairly well defined,
while that of the secondary is less reliable. The continuous lines are
the ZAMS and evolutionary tracks interpolated for the measured masses, while
the dotted and broken lines are the isochrones at 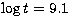 and and
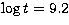 respectively respectively |
![\begin{figure}
\includegraphics [width=8.5cm]{ds7203f10.eps}\end{figure}](/articles/aas/full/1998/11/ds7203/Timg80.gif) |
Figure 10:
Radial-velocity curve of HD 96391. The period is
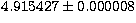 days days |
This star was classified A4-F0-F3 by Abt (1984). It is also an SB2 system
with very similar companions. Unfortunately, we do not have Geneva
photometry for that star, but Strömgren photometry![[*]](/icons/foot_motif.gif) done by Olsen (1983) and retrieved using the General Catalogue of Photometric
Data (Mermilliod et al. 1997) gives
done by Olsen (1983) and retrieved using the General Catalogue of Photometric
Data (Mermilliod et al. 1997) gives 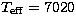 K,
K, 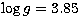 through the calibration of Moon & Dworetsky (1985), and
through the calibration of Moon & Dworetsky (1985), and 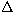 m0 = -0.051,
m0 = -0.051,
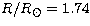 , MV = 2.66,
, MV = 2.66, 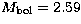 and
and
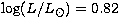 through older calibrations included in
Moon's (1985)
code. We have 36 CORAVEL observations of this star (Tables 11 and 12); the
orbital elements are listed in Table 1 and the
through older calibrations included in
Moon's (1985)
code. We have 36 CORAVEL observations of this star (Tables 11 and 12); the
orbital elements are listed in Table 1 and the
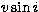 value of each component is given in Table 2. The i
angle remains unknown, since that star is not known
as an eclipsing binary.
value of each component is given in Table 2. The i
angle remains unknown, since that star is not known
as an eclipsing binary.
On the other hand, the Hipparcos parallax is 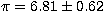 mas, which implies a distance d = 152 pc taking into account the Lutz-Kelker
correction -0.07. Furthermore,
from the reddening maps of Lucke (1978), a colour excess E(B-V) = 0.029
appears reasonable, so we adopt
mas, which implies a distance d = 152 pc taking into account the Lutz-Kelker
correction -0.07. Furthermore,
from the reddening maps of Lucke (1978), a colour excess E(B-V) = 0.029
appears reasonable, so we adopt 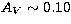 ; to correct for the duplicity,
the apparent visual magnitude is increased by 0.75 mag (so the result will
relate to an average component), and one obtains
MV=1.82,
; to correct for the duplicity,
the apparent visual magnitude is increased by 0.75 mag (so the result will
relate to an average component), and one obtains
MV=1.82, 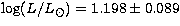 , and
by interpolation in theoretical evolutionary tracks,
, and
by interpolation in theoretical evolutionary tracks, 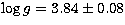 dex,
dex, 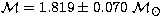 and
and 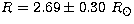 .The agreement of the
.The agreement of the 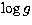 value obtained here with that given by the uvby photometry is excellent
(the photometric luminosity is far off, but is obtained through an older
calibration). Once again, this system appears close to the end of its life
on the main sequence.
It is now possible to estimate the orbital inclination i
by comparing
value obtained here with that given by the uvby photometry is excellent
(the photometric luminosity is far off, but is obtained through an older
calibration). Once again, this system appears close to the end of its life
on the main sequence.
It is now possible to estimate the orbital inclination i
by comparing 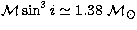 with
with
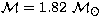 and the result is
and the result is 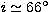 .This precludes eclipses, which would need an orbital inclination larger
than
.This precludes eclipses, which would need an orbital inclination larger
than 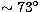 to occur. The individual masses are about
to occur. The individual masses are about
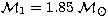 and
and 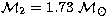 .The average equatorial velocity computed from the radius obtained above
and from the assumption of synchronism is 27.7 kms-1, which translates
into
.The average equatorial velocity computed from the radius obtained above
and from the assumption of synchronism is 27.7 kms-1, which translates
into 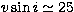 kms-1. This value may be compared with the
observed
kms-1. This value may be compared with the
observed 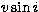 's of both companions (Table 2), if the spin axes are
perpendicular to the orbital plane: the observed values are smaller than those
predicted by synchronism via the radius estimate, but the
's of both companions (Table 2), if the spin axes are
perpendicular to the orbital plane: the observed values are smaller than those
predicted by synchronism via the radius estimate, but the 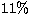 error on the
latter is large enough to accomodate both results within two
error on the
latter is large enough to accomodate both results within two 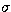 .The system is very probably synchronised.
.The system is very probably synchronised.


Up: Multiplicity among peculiar A stars,
Copyright The European Southern Observatory (ESO)
![\begin{figure}
\includegraphics [width=8.5cm]{ds7203f7.eps}\end{figure}](/articles/aas/full/1998/11/ds7203/Timg57.gif)
![\begin{figure*}
\centering
\includegraphics [width=16cm]{ds7203f8.eps}\end{figure*}](/articles/aas/full/1998/11/ds7203/Timg58.gif)
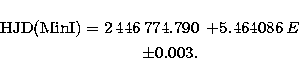

![]() and
and ![]() , we interpolated the linear
limb-darkening coefficient u from the tables of Van Hamme (1993).
With the
available photometric data, it is impossible to fit simultaneously all the
interesting parameters, namely the central surface brightness of the secondary
, we interpolated the linear
limb-darkening coefficient u from the tables of Van Hamme (1993).
With the
available photometric data, it is impossible to fit simultaneously all the
interesting parameters, namely the central surface brightness of the secondary
![]() , the radius
, the radius ![]() of the primary, the ratio k of the radii and the
orbital inclination i. This is a well-known difficulty for all systems
(even well detached ones) where both components are nearly identical, even when
the eclipses are deep. Another type of data has to be used to constrain the
ratio of radii, because the latter may be changed from e.g. 0.6 to 1.4,
without any change in the rms scatter of the residuals. We do not have
detailed spectroscopic informations, but the CORAVEL data allow to have a
rough guess of the k ratio in the two following ways:
of the primary, the ratio k of the radii and the
orbital inclination i. This is a well-known difficulty for all systems
(even well detached ones) where both components are nearly identical, even when
the eclipses are deep. Another type of data has to be used to constrain the
ratio of radii, because the latter may be changed from e.g. 0.6 to 1.4,
without any change in the rms scatter of the residuals. We do not have
detailed spectroscopic informations, but the CORAVEL data allow to have a
rough guess of the k ratio in the two following ways:
![\begin{tabular}
{cl} \hline
\multicolumn{1}{c}{Parameter}
& \multicolumn{1}{c}{...
...L_1+L_2)$& 0.62 \\ $\sigma_{\rm res}$\space [mag]&0.0073 \\ \hline\end{tabular}](/articles/aas/full/1998/11/ds7203/img71.gif)
![]() mas or d = 258-50+82 pc; however,
the discrepancy cannot be considered significant since it remains largely
within two sigmas. The distance deduced from the fundamental radii and
photometric effective temperatures is almost twice more accurate than that
given by Hipparcos (the error has been estimated using the usual propagation
formula applied to the distance modulus). It is interesting that the fundamental
mas or d = 258-50+82 pc; however,
the discrepancy cannot be considered significant since it remains largely
within two sigmas. The distance deduced from the fundamental radii and
photometric effective temperatures is almost twice more accurate than that
given by Hipparcos (the error has been estimated using the usual propagation
formula applied to the distance modulus). It is interesting that the fundamental ![]() value we find for the primary, which is quite reliable, is in excellent agreement with the value obtained from both Geneva and
value we find for the primary, which is quite reliable, is in excellent agreement with the value obtained from both Geneva and ![]() colour
indices.
colour
indices.
![]() and 9.2. The primary is clearly at the end of its life on the Main Sequence,
and the secondary is probably somewhat evolved too. In view of the shape
of the isochrones, one can easily understand why the secondary is slightly
hotter than the primary. Clearly, a more complete and precise
lightcurve is needed, especially to give a more accurate, fundamental estimate
of the radii and to assess thereby the validity of the assumption of
synchronism.
and 9.2. The primary is clearly at the end of its life on the Main Sequence,
and the secondary is probably somewhat evolved too. In view of the shape
of the isochrones, one can easily understand why the secondary is slightly
hotter than the primary. Clearly, a more complete and precise
lightcurve is needed, especially to give a more accurate, fundamental estimate
of the radii and to assess thereby the validity of the assumption of
synchronism.
![]() mas, which implies a distance d = 152 pc taking into account the Lutz-Kelker
correction -0.07. Furthermore,
from the reddening maps of Lucke (1978), a colour excess E(B-V) = 0.029
appears reasonable, so we adopt
mas, which implies a distance d = 152 pc taking into account the Lutz-Kelker
correction -0.07. Furthermore,
from the reddening maps of Lucke (1978), a colour excess E(B-V) = 0.029
appears reasonable, so we adopt ![]() ; to correct for the duplicity,
the apparent visual magnitude is increased by 0.75 mag (so the result will
relate to an average component), and one obtains
MV=1.82,
; to correct for the duplicity,
the apparent visual magnitude is increased by 0.75 mag (so the result will
relate to an average component), and one obtains
MV=1.82, ![]() , and
by interpolation in theoretical evolutionary tracks,
, and
by interpolation in theoretical evolutionary tracks, ![]() dex,
dex, ![]() and
and ![]() .The agreement of the
.The agreement of the ![]() value obtained here with that given by the uvby photometry is excellent
(the photometric luminosity is far off, but is obtained through an older
calibration). Once again, this system appears close to the end of its life
on the main sequence.
It is now possible to estimate the orbital inclination i
by comparing
value obtained here with that given by the uvby photometry is excellent
(the photometric luminosity is far off, but is obtained through an older
calibration). Once again, this system appears close to the end of its life
on the main sequence.
It is now possible to estimate the orbital inclination i
by comparing ![]() with
with
![]() and the result is
and the result is ![]() .This precludes eclipses, which would need an orbital inclination larger
than
.This precludes eclipses, which would need an orbital inclination larger
than ![]() to occur. The individual masses are about
to occur. The individual masses are about
![]() and
and ![]() .The average equatorial velocity computed from the radius obtained above
and from the assumption of synchronism is 27.7 kms-1, which translates
into
.The average equatorial velocity computed from the radius obtained above
and from the assumption of synchronism is 27.7 kms-1, which translates
into ![]() kms-1. This value may be compared with the
observed
kms-1. This value may be compared with the
observed ![]() 's of both companions (Table 2), if the spin axes are
perpendicular to the orbital plane: the observed values are smaller than those
predicted by synchronism via the radius estimate, but the
's of both companions (Table 2), if the spin axes are
perpendicular to the orbital plane: the observed values are smaller than those
predicted by synchronism via the radius estimate, but the ![]() error on the
latter is large enough to accomodate both results within two
error on the
latter is large enough to accomodate both results within two ![]() .The system is very probably synchronised.
.The system is very probably synchronised.