This bright A2 Sr star was already known as an SB1 system. Its rotational period, known from its photometric variability, is 69.43 days (Rakosch & Fiedler 1978). Renson (1966) found an orbital period of 106.3 days and published the radial-velocity curve, but not the orbital parameters. A total of 107 measurements have been made over almost 5000 days (Table 6), which confirms the 106 days period (see Fig. 1). However, the residuals are larger than expected from the precision of the measurements, and follow a very clear trend (see Fig. 2). The presence of a third component is certain, although its period is so long that we could not cover even one cycle. The orbital parameters of the primary are given in Table 1. This is the second spectroscopic triple system known among Ap stars, after the SiMg star HD 201433 whose periods are much shorter (see the catalogue of Tokovinin 1997).
The projected rotational velocity estimated from the width of the autocorrelation dip (Benz & Mayor 1984) is given in Table 2, with the restriction that in principle, such a quantity can only represent an upper limit to the true
The Hipparcos parallax of this star is ![]() mas
(Perryman et al. 1997); this translates into a distance d=232 pc, after having
applied a Lutz-Kelker correction (Lutz & Kelker 1973)
mas
(Perryman et al. 1997); this translates into a distance d=232 pc, after having
applied a Lutz-Kelker correction (Lutz & Kelker 1973) ![]() which
takes into account the exponential decrease of stellar density in the
direction perpendicular to the galactic plane. On the other hand, the visual
absorption estimated from Geneva photometry is Av = 0.13. Assuming a
contribution of about 0.23 magnitudes of the companions to the visual magnitude
of the system, the apparent magnitude of the primary alone is V=6.92, and
finally we obtain an absolute magnitude
which
takes into account the exponential decrease of stellar density in the
direction perpendicular to the galactic plane. On the other hand, the visual
absorption estimated from Geneva photometry is Av = 0.13. Assuming a
contribution of about 0.23 magnitudes of the companions to the visual magnitude
of the system, the apparent magnitude of the primary alone is V=6.92, and
finally we obtain an absolute magnitude ![]() for this component.
Adopting
for this component.
Adopting ![]() K (Adelman et al. 1995) and interpolating in
the evolutionary tracks of Schaller et al. (1992) for a solar metallicity
Z=0.018
K (Adelman et al. 1995) and interpolating in
the evolutionary tracks of Schaller et al. (1992) for a solar metallicity
Z=0.018![]() (and for a moderate overshooting distance
(and for a moderate overshooting distance ![]() ),
one obtains
),
one obtains ![]() ,
, ![]() (g in cgs units) and
(g in cgs units) and ![]() .Although the uncertainties are fairly
large, the primary is evolved and on the verge of leaving the Main Sequence; it
is satisfying that our small
.Although the uncertainties are fairly
large, the primary is evolved and on the verge of leaving the Main Sequence; it
is satisfying that our small ![]() value agrees with the spectroscopic
estimate of Adelman et al. (1995) who gave
value agrees with the spectroscopic
estimate of Adelman et al. (1995) who gave ![]() .
.
![\begin{figure}
\includegraphics [width=8.5cm]{ds7203f4.eps}\end{figure}](/articles/aas/full/1998/11/ds7203/Timg25.gif) |
Figure 4:
Radial-velocity curve of HD 137909 including data published by
Kamper et al. (1990), by Neubauer (1944)
and by Oetken & Orwert (1984).
A correction of |
Thanks to the Hipparcos satellite, ![]() CrB has now a very precise parallax
CrB has now a very precise parallax
![]() mas which allows to compute the linear semi-major axis of the relative orbit from the angular semi-major axis obtained by speckle
interferometry (
mas which allows to compute the linear semi-major axis of the relative orbit from the angular semi-major axis obtained by speckle
interferometry (![]() mas). Since the inclination angle
mas). Since the inclination angle
![]() of the orbit is known from speckle
interferometry and the quantity
of the orbit is known from speckle
interferometry and the quantity ![]() is known from CORAVEL
measurements, the semi-major axis of the absolute orbit of the companion can be
computed:
is known from CORAVEL
measurements, the semi-major axis of the absolute orbit of the companion can be
computed:
| (1) |
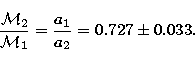 |
(2) |
The HR diagram is shown in Fig. 6. Strangely enough, the agreement between
the observed location of ![]() CrB and the evolutionary track at the observed
dynamical mass is very poor: both the primary and the secondary (if we
rely on
CrB and the evolutionary track at the observed
dynamical mass is very poor: both the primary and the secondary (if we
rely on ![]() ) appear overluminous compared to the
evolutionary tracks drawn for their mass. Considered alone, the primary might
well be at the very tip of the blue hook at the core-hydrogen exhaustion phase,
which would reconcile within one
) appear overluminous compared to the
evolutionary tracks drawn for their mass. Considered alone, the primary might
well be at the very tip of the blue hook at the core-hydrogen exhaustion phase,
which would reconcile within one ![]() its observed and theoretical locations
in the HR diagram. Its logarithmic age might then be 9.05 dex instead
of 8.9. However, the secondary (indicated in Fig. 6 as a dot arbitrarily
placed along the abcissa on the isochrone
its observed and theoretical locations
in the HR diagram. Its logarithmic age might then be 9.05 dex instead
of 8.9. However, the secondary (indicated in Fig. 6 as a dot arbitrarily
placed along the abcissa on the isochrone ![]() ) seems overluminous as
well, making the puzzle more complicated but also more interesting, and
certainly well worth further investigations. Unfortunately, it is not possible
to test completely the position of the secondary because of its unknown
colours
) seems overluminous as
well, making the puzzle more complicated but also more interesting, and
certainly well worth further investigations. Unfortunately, it is not possible
to test completely the position of the secondary because of its unknown
colours![]() .
Such an information would be most interesting to test the idea of
Hack et al. (1997) that the companion might be a
.
Such an information would be most interesting to test the idea of
Hack et al. (1997) that the companion might be a ![]() Boo star with
Boo star with
![]() K, although such a hypothesis appears difficult to
maintain in view of Fig. 6.
K, although such a hypothesis appears difficult to
maintain in view of Fig. 6.
The semi-major axis of the orbit of the binary's photocenter is given in the
Hipparcos and Tycho Catalogues (Perryman et al. 1997). This allows an
independant test of the magnitude difference ![]() : assuming the
photocenter to be defined by E1 x1 = E2 x2, where E1 and E2 are the
respective brightnesses of the components in the
: assuming the
photocenter to be defined by E1 x1 = E2 x2, where E1 and E2 are the
respective brightnesses of the components in the ![]() passband and x1, x2
the distances of the components to the photocenter such that
x1+x2=a1+a2=a, one obtains
passband and x1, x2
the distances of the components to the photocenter such that
x1+x2=a1+a2=a, one obtains ![]() au, on the basis
of Tokovinin's
au, on the basis
of Tokovinin's ![]() (one has a0= a1-x1). This is in
rough agreement (within three sigmas) with
(one has a0= a1-x1). This is in
rough agreement (within three sigmas) with ![]() au given
in the Hipparcos catalogue. Our estimate assumes a companion with
au given
in the Hipparcos catalogue. Our estimate assumes a companion with
![]() K and takes into account the colour equation
between
K and takes into account the colour equation
between ![]() and V (Vol. 2, p. 59 of Perryman et al. 1997)
which leads to
and V (Vol. 2, p. 59 of Perryman et al. 1997)
which leads to
![]() . Increasing
. Increasing ![]() by about 0.2 magnitudes
would bring perfect agreement. Unfortunately, Tokovinin (1985)
do not give any
error estimate on
by about 0.2 magnitudes
would bring perfect agreement. Unfortunately, Tokovinin (1985)
do not give any
error estimate on ![]() .
.
Copyright The European Southern Observatory (ESO)