4 Results and discussion

The previously described calibration curve was applied to 50 CP2 stars from the catalog of stellar spectrophotometry (Adelman et al. 1989) and to 18 CP2 stars from the Pulkovo spectrophotometric catalog of bright stars (Alekseeva et al. 1996). For these stars the HD number, name, peculiarity according to General Catalogue of Ap and Am stars by Renson et al. (1991), number of the visual scans, temperature and error obtained from the relationships (1) and (2), respectively are given in Table 1. An asterisk following $T_\mathrm{eff}$($\it\Phi_\mathrm{u}$) means that this datum was computed from energy distribution of the PSC.

To test the validity of the proposed method of determination of $T_\mathrm{eff}$ for CP2 stars, the temperatures derived from $\it\Phi_\mathrm{u}$ were compared with those derived by the infrared flux method, by the Stepien & Dominiczak (1989) method and with temperatures derived from (B2-G) color index of Geneva photometry.

4.1 A comparison with infrared flux method determinations

In the literature there are five papers concerning the CP2 stars where the effective temperatures are derived by the infrared flux method. These papers are those by Shallis & Blackwell (1979), Shallis et al. (1985), Lanz (1985), Glushneva (1987), Megessier (1988). The star HD 35497 ($\beta$ Tau) is mentioned in the paper by Underhill et al. (1979), where the effective temperatures are derived by the same way. The effective temperature for this star derived by Underhill et al. was taken into consideration as well. If there are several determinations of $T_\mathrm{eff}$ by IRFM for individual star then the latest determination is considered. For example, all the CP2 stars investigated by Lanz are mentioned in Mégessier's paper. For the common stars with those of Table 1, their $T_\mathrm{eff}$values and the references are given in Cols. 7 and 8, respectively. The values of $T_\mathrm{eff}$ derived from $\it\Phi_\mathrm{u}$are compared with those obtained by IRFM for 13 common stars (see Fig. 2, where the straight line denotes the relation $T_\mathrm{eff}$(IRFM) = $T_\mathrm{eff}$($\it\Phi_\mathrm{u}$)). One can see, that the agreement appears to be very good. It is confirmed by the following results: $\Delta$$T_\mathrm{eff}$ = 41$\pm$127 K, r  = 0.972, $\alpha$ = 0.904. Only for two cool stars: HD 176232 (10 Aql) and HD 201601 ($\gamma$ Equ) the temperatures derived by Shallis et al. (1985) and by Shallis & Blackwell (1979), respectively, are relatively low. Glushneva (1987) has noted the same disagreement with Shallis & Blackwell (1979) determinations. So she has redetermined the effective temperature of the star HD 112185 ($\varepsilon$ UMa), obtaining a value of 9470 K, which is higher than that of 8920 K by Shallis & Blackwell. For this star the effective temperature derived from $\it\Phi_\mathrm{u}$ is equal 9340 K, this value is in agreement with the temperature obtained by Glushneva. Hauck & North (1993) also noted that the temperature derived by Shallis & Blackwell (1979) for the star HD 358 ($\alpha$ And) is relatively low. Finally, the effective temperatures derived from $\it\Phi_\mathrm{u}$ (with the exception of two cool stars) are in the excellent agreement with $T_\mathrm{eff}$ obtained by IRFM.

  

Figure 2: Comparison of $T_\mathrm{eff}$ derived from $\it\Phi_\mathrm{u}$ with those derived by infrared flux method

4.2 A comparison with the determinations obtained by the method of Stepien $\&$ Dominiczak

Stepien & Dominiczak (1989) proposed the new method to determine the effective temperatures of CP2 stars. From a fit of the observed visual energy distribution of CP stars with a solar-composition model, they derived the flux deficit relative to the model, and then a temperature correction to the model temperature. Practically, the method includes two steps: first, the model temperature $T_\mathrm{M}$ is found from the detailed fit of the Kurucz's model to the observed visual energy distribution and second, the obtained $T_\mathrm{M}$ should be transformed to $T_\mathrm{eff}$ by using the relation, defined by Stepien & Dominiczak as:

$${T_{\rm eff}}=1600 + 0.80 \cdot {T}_{\rm M}.$$ (3)

They derived this relation by using twelve CP stars with available visual and UV energy distributions. In order to have wider sample of stars for the comparison, this method was applied to the model temperatures obtained by Adelman (1985). He derived temperatures for 49 CP2 stars from a fit of the Kurucz's model to the observed ultraviolet and visual energy distributions as well as to the Balmer jump and received three temperatures: T (UV), T (PC) and T (BJ) for each star. All the CP2 stars investigated by Stepien & Dominiczak are presented in Adelman's paper. This allows to compare the Paschen continuum temperature - T (PC) and the Balmer jump temperature - T (BJ) derived by Adelman with the $T_\mathrm{M}$ derived by Stepien & Dominiczak. For five stars the values of T (PC) and T (BJ) are equal and in the good agreement with $T_\mathrm{M}$. But, the comparison of all 12 stars shows that the $T_\mathrm{M}$ is 319 K cooler than the T (BJ) and 208 K hotter than T (PC). On the other hand, the computed as a mean value from the T (PC) and the T (BJ) model temperatures are in good agreement with $T_\mathrm{M}$ derived by Stepien & Dominiczak. The mean difference between two sets of data is equal to 111 K.

Based on this temperature comparison as well as on the conclusions given by Mégessier (1988) and by Stepien & Dominiczak (1989) on importance of the Balmer jump in the determination of the temperature, the values of $T_\mathrm{M}$ as mean from the T (PC) and the T (BJ) were calculated for all stars of Table 2 from paper of Adelman (1985). After that, this mean value of $T_\mathrm{M}$ was corrected for the blanketing effect by using Eq. (3). The resulting temperatures ($T_\mathrm{eff}$(S&D)) are reported in Col. 9 of Table 1. Figure 3 gives a plot of $T_\mathrm{eff}$ derived from $\it\Phi_\mathrm{u}$ versus $T_\mathrm{eff}$(S&D) for 47 common stars. The straight line corresponds to the relation $T_\mathrm{eff}$($\it\Phi_\mathrm{u}$)=$T_\mathrm{eff}$(S&D). As one can see from Fig. 3, for most of the stars the agreement between $T_\mathrm{eff}$($\it\Phi_\mathrm{u}$) and $T_\mathrm{eff}$(S&D) appears to be very good, but for some stars the difference between two determinations is more than one sigma error. This discrepancy can be the result of the errors in the computation of the mean value of $T_\mathrm{M}$from the T (PC) and the T (BJ) or the value of $\it\Phi_\mathrm{u}$ in our method for individual stars. The effect of variability of these CP2 stars should be excluded, because for both methods the same observed energy distribution was used. Basically, there are no systematical differences between two sets of the data that is confirmed by the following results: $\Delta$$T_\mathrm{eff}$ = 38$\pm$69 K, r  = 0.952, $\alpha$ = 0.965.

  

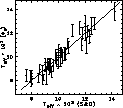Figure 3: Comparison of $T_\mathrm{eff}$ derived from $\it\Phi_\mathrm{u}$ with those derived by the method proposed by Stepien & Dominiczak (1989)

4.3 A comparison with photometric determinations

The photometric methods to determine $T_\mathrm{eff}$ of CP stars were proposed in many photometric systems. As a rule, these methods are based on colors in the visible region of spectrum, thus it is necessary to correct the color temperature for blanketing effect to obtain an effective one. Comparisons of $T_\mathrm{eff}$derived by IRFM or by the method of Stepien & Dominiczak with $T_\mathrm{eff}$($B\mathrm{2}-G$) and $T_\mathrm{eff}(X,Y)$ given by Hauck & North (1993) show that ($B\mathrm{2}-G$) color index is a very good estimator of $T_\mathrm{eff}$for CP2 stars. Moreover the color index ($B\mathrm{2}-G$)can be used without a correction for the blanketing effect, because this effect is included in the temperature calibration, while the reddening - free parameters X and Y should be corrected for that. It should be noted, that the ($B\mathrm{2}-G$) color index is to be corrected for the interstellar reddening, but the parameters X and Y are reddening-free. In order to estimate photometrically the effective temperatures of CP2 stars the ($B\mathrm{2}-G$) color index was used. The values of $T_\mathrm{eff}$($B\mathrm{2}-G$) were taken from Table 1 of Hauck & North paper for the sample of 21 common stars. In addition, the values of $T_\mathrm{eff}$($B\mathrm{2}-G$)for the 38 stars are computed according to the procedure described by Hauck & North (1993) and by using the photometric data from the paper by Hauck & North (1982). The values of $T_\mathrm{eff}$($B\mathrm{2}-G$) for the 59 common stars are presented in Col. 10 of Table 1. Figure 4 gives a plot of the $T_\mathrm{eff}$ derived from $\it\Phi_\mathrm{u}$ versus $T_\mathrm{eff}$($B\mathrm{2}-G$). One can see, there are no systematic differences between two sets of the data, though the scattering of the points in Fig. 4 is high enough (up to 1000 K), especially for the stars with $T_\mathrm{eff}\gt 9500$ K. So, the comparison of $T_\mathrm{eff}$ derived from $\it\Phi_\mathrm{u}$with $T_\mathrm{eff}$($B\mathrm{2}-G$) shows that for 28 stars with $T_{\rm eff}\leq9500$ K the agreement between two sets of data is very good. The mean difference between $T_\mathrm{eff}$($\it\Phi_\mathrm{u}$)and $T_\mathrm{eff}$($B\mathrm{2}-G$) is 42$\pm$80 K. For all the stars in our sample the mean effective temperature difference is $\Delta$$T_\mathrm{eff}$ =  $T_\mathrm{eff}$($\it\Phi_\mathrm{u})-T_\mathrm{eff}$($B\mathrm{2}-G$)  = 102$\pm$76 K, with a linear correlation coefficient r  = 0.938, and $\alpha$ = 0.975 for the slope of the regression line of $T_\mathrm{eff}$($\it\Phi_\mathrm{u}$) versus $T_\mathrm{eff}$($B\mathrm{2}-G$). The comparison of the stars with $T_\mathrm{eff}\gt 9500$ K shows that $T_\mathrm{eff}$($B\mathrm{2}-G$) are slightly less than $T_\mathrm{eff}$($\it\Phi_\mathrm{u}$). For these stars the mean difference $\Delta$$T_\mathrm{eff}$ is equal 154$\pm$124 K. Probably this difference can be explained by the correction of ($B\mathrm{2}-G$) color index for interstellar reddening because it is very hard to separate the effects due to interstellar reddening from those due to the non-normal energy distribution of CP2 stars. It is also confirmed by the conclusion of Hauck & North (1993) that for CP2 stars with $T_\mathrm{eff}\gt 9500$ K the values of $T_\mathrm{eff}$($B\mathrm{2}-G$) are less reliable. For these stars they propose to use the reddening-free parameters X and Y.

  

Figure 4: Comparison of $T_\mathrm{eff}$ derived from $\it\Phi_\mathrm{u}$ with those derived from $(B\mathrm{2}-G)$ color index of Geneva photometry

The X and Y parameters of Geneva photometry are primarily related to $T_\mathrm{eff}$ and $\log g$ respectively, but they can be affected by the stars's peculiarity, especially for CP2 stars cooler than 11000 K (North & Cramer 1984). However, for CP2 stars Hauck & North (1993) propose to use the X and Y parameters and transform $T_\mathrm{eff}(X,Y)$ to $T_\mathrm{eff}$ through relation between $T_\mathrm{eff}(X,Y)$ and $T_\mathrm{eff}$ obtained by these authors. On the other hand, according to results presented by Lanz et al. (1993) the significant scattering (up to 2000 K) can be observed for some values of X and the uncertainties in temperatures are rather large (about 1000 K). In other words, the X parameter may give the same scattering of points when comparing $T_\mathrm{eff}$($\it\Phi_\mathrm{u}$) with $T_\mathrm{eff}(X)$.

Generally, there are no significant systematical differences between the temperatures derived from $\it\Phi_\mathrm{u}$ and those derived from fluxes by other methods. The temperature calibration derived for B, A and F main sequence stars is applicable to CP2 stars as well. The temperature derived from $\it\Phi_\mathrm{u}$ for CP2 stars may be identified with their effective one, because the influence of the stars's peculiarity on the Balmer continuum slope near the Balmer jump is negligible.

Taking into account the observational uncertainties of the slope, the calibration errors, as well as the errors for the mean interstellar extinction law and for the value E(B-V) for the reddened stars the error of $T_\mathrm{eff}$ are calculated for each star of our sample. The statistical errors of the temperature determination vary from star to star with their values ranging from 5% to 10%. As a rule, the large errors in the temperature determination related to the stars with large photometric variations.

In our study only Si, Cr and SiCrEu types of CP stars were used, but this method can be extended to other types of CP stars when a blanketing effect is less and the temperature derived from $\it\Phi_\mathrm{u}$ should be close to the effective one. For example, Hauck & North (1993) have shown that the colour temperature of CP1 (Am) and of CP4 (He-wk) stars may be identified with their effective temperature. In the case of CP3 (MgMn) stars it is less clear, because for these stars there are a few of direct $T_\mathrm{eff}$ determinations. The fact that their UV flux is normal (Jamar et al. 1978) suggests that the colour temperature of CP3 stars may be also identified with their effective one.