3 The method description

In this section the method is proposed to derive the effective temperatures of CP stars by using the slope of the Balmer continuum near the Balmer jump. It is well known that the first order difference between energy distribution of "normal" main sequence stars and peculiar stars is caused by extra blocking of the flux in the far-UV and the redistribution of it in the longer wavelengths. The presented method implies the existence of a region of wavelengths between far-UV and visual regions with the same energy distribution for normal and peculiar stars. The comparison of the observed energy distributions with the best fitting models for twelve CP stars given by Stepien & Dominiczak (1989) supports this assumption and shows that the slope of spectra in the Balmer continuum between 3200 Å and 3600 Å  both for the observed energy distribution of CP stars and for the models is identical (see Fig. 2 of Stepien & Dominiczak 1989). Only two stars HD 65339 and HD 125248 display the flux disagreement in this region of spectra, but the slopes of observed and theoretical energy distributions are similar for both stars.

From the theoretical point of view the flux in the Balmer continuum near the Balmer jump is formed in the outer layers of stellar atmosphere, because the absorption coefficient is high here and, probably, the effects caused by the peculiarity of CP stars are lesser. On the other hand, the Paschen continuum and the far-UV are formed in the inner layers where the effects of peculiarity of CP stars (the $\lambda$ 1400, $\lambda$ 4200 and $\lambda$ 5200 broad continuum features, the photometric and magnetic field variability) are significant. The computations held by Leckrone et al. (1974) and by Muthsam (1978, 1979) show that there exists a wavelength $\lambda_\mathrm{tr}$ such that for $\lambda$ < $\lambda_\mathrm{tr}$ the flux of radiation is suppressed relative to the flux of a normal star with the same effective temperature, whereas for $\lambda$ > $\lambda_\mathrm{tr}$ it is enhanced. Note that the location of $\lambda_\mathrm{tr}$ is in the Balmer continuum near the Balmer jump, which is used for the determination of the effective temperatures (Sokolov 1995).

  

Table 1: Effective temperatures of CP2 (Ap magnetic) stars

For determination of the shape of the continuum at both sides of the Balmer jump, an iterative procedure was used that permits to exclude absorption lines, as described by Sokolov (1995). The values of the Balmer continuum parameters were computed by using the linear approximation in the form $\Delta{m}_{\lambda}$ = $\it\Psi_\mathrm{u}$ +  $\it\Phi_\mathrm{u}$ $\cdot$ (1/$\lambda$). Here $\Delta{m}_{\lambda}$ = ${m}_{\lambda}- {m}_{\rm 5550\ \mbox {\AA}}$,the parameter $\it\Phi$$_\mathrm{u}$ is the slope of the Balmer continuum and $\it\Psi$$_\mathrm{u}$ is the constant term of the linear approximation. In the paper by Sokolov (1995) it is shown that the slope of the Balmer continuum between 3200 Å  and 3600 Å  is a very good indicator of the effective temperature for B, A and F main sequence stars. The linear calibration curve between ${\it\Theta}_\mathrm{eff}=5040/T_\mathrm{eff}$ and $\it\Phi_\mathrm{u}$is established by using the standard stars with well known temperatures taken from Code et al. (1976) and Malagnini et al. (1986). This temperature calibration can be applied in the wide temperature interval from 6000 K to 27000 K.

Based on the theoretical prediction, as well as on the fact that the slope of the Balmer continuum near the Balmer jump of models and CP stars is identical, this observational parameter is used for determination of the effective temperatures of CP stars. The temperature calibration of B, A and F main sequence stars (Sokolov 1995) is applied to the CP stars, which was defined as:

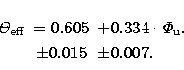$$\begin{eqnarray} {\it\Theta}_{\rm eff} &=0.605 &+0.334\cdot{\it\Phi}_{\rm u}. \\ &\pm0.015 &\pm0.007. \nonumber \end{eqnarray}$$ (1)

The errors on effective temperatures are computed by taking into account the contributions from different terms, according to the errors' formula for the standard propagation theory:

$${\sigma}_{T_{\rm eff}}=A \cdot [{\sigma}_{\rm a}^2 + {\it\Ph... ...it E}^2{\sigma}_{\rm S}^2 +S^2{\sigma}_{\rm E}^2)]^{1 \over 2}$$ (2)

where A=$T_\mathrm{eff}$²/5040, $\rm \sigma_{a}$and $\rm \sigma_{b}$ refer to the errors of the calibration coefficients and $\sigma_{\Phi}$ is the error in the slope of the energy distribution. The values of errors for the mean interstellar extinction law - $\rm \sigma_{S}$ and for the colour excess $E(B-V) - \rm \sigma_{E}$ are estimated in the paper (Sokolov 1995) and are equal to 0.048 and 0.03, respectively.

Generally, the least-squares procedure is used in order to compute the values of the Balmer continuum parameters near the Balmer jump. The effective temperatures of the CP stars are derived from the slope of spectra in the Balmer continuum by using Eq. (1). The errors on $T_\mathrm{eff}$ were computed by using Eq. (2). It should be noted, that for the stars with E(B-V) < 0.03, only the errors in the calibration coefficients and the error in the slope of the energy distribution are taken into account. For stars with E(B-V) > 0.03 the errors on $T_\mathrm{eff}$ were computed taking into account additionally the values $\rm \sigma_{S}$ and $\rm \sigma_{E}$.For these stars the average energy distribution corrected for interstellar reddening was used from the catalog of stellar spectrophotometry.