To perform a statistical analysis, we introduce the time interval ![]() which is the difference between the measured time
interval
which is the difference between the measured time
interval ![]() given by Eq. (1) and the computed
travel time
given by Eq. (1) and the computed
travel time ![]() .
The residual precision
.
The residual precision ![]() is
defined by the root mean
square of
is
defined by the root mean
square of ![]() , measured in stable conditions. Since the
measurements are corrected by the term
, measured in stable conditions. Since the
measurements are corrected by the term ![]() at a period
at a period
![]() , all the
instrumental precisions have to be evaluated over a period
, all the
instrumental precisions have to be evaluated over a period ![]() .This condition concerns the start and the return detectors, the laser, and
the timers. The accuracy of the measurement
.This condition concerns the start and the return detectors, the laser, and
the timers. The accuracy of the measurement ![]() illustrates the
error between the real distance and the measured distance. It depends on the
precision of the measurement and on the unknown systematic errors. One
obtains only an estimation of the accuracy. The measurements being degraded
by some noises, which are time dependant, it is convenient to introduce the
time stability
illustrates the
error between the real distance and the measured distance. It depends on the
precision of the measurement and on the unknown systematic errors. One
obtains only an estimation of the accuracy. The measurements being degraded
by some noises, which are time dependant, it is convenient to introduce the
time stability ![]() of these measurements over a period
of these measurements over a period ![]() . This can be computed by the Time variance
TVAR (Allan et al. 1991). To evaluate the precision, the accuracy and
the stability, we first present the different uncertainty sources involved
in the lunar measurement.
. This can be computed by the Time variance
TVAR (Allan et al. 1991). To evaluate the precision, the accuracy and
the stability, we first present the different uncertainty sources involved
in the lunar measurement.
The laser characteristics are:
- type: YAG
- 4 pulses at a rate of 10 Hz
- ![]() nm and 1064 nm
nm and 1064 nm
- FWHM = 70 ps
- Energy: 75 mJ @ 532 nm; 75 mJ @ 1064 nm per pulse.
The mean value of the light pulse width is in the range of 70 ps. The
shape of the pulse is Gaussian. The pulse width experiences some variations
between 50 ps and 90 ps, caused by temperature inhomogeneities in the
laser cavity. These variations are only encountered during the warm-up of
the laser and a stable regime is obtained after thirty minutes. The start
detector response is sensitive to the variation of the pulse width since the
detector receives a large amount of photons. The variation ![]() of the
laser width introduces a shift equal to
of the
laser width introduces a shift equal to ![]() between the pulse
centre and the photo-detector electrical response. The laser width root mean
square of about 50000 laser pulses, measured in stable conditions, is 9 ps. This quantity will introduce in the global error budget the term
between the pulse
centre and the photo-detector electrical response. The laser width root mean
square of about 50000 laser pulses, measured in stable conditions, is 9 ps. This quantity will introduce in the global error budget the term ![]() ps rms. The return detector response is sensitive
to the width of the laser pulse since it is working in a single photon mode.
The term added to the error budget, deduced from the laser FWHM, is
ps rms. The return detector response is sensitive
to the width of the laser pulse since it is working in a single photon mode.
The term added to the error budget, deduced from the laser FWHM, is ![]() ps rms. Figure 2
ps rms. Figure 2
![\begin{figure}
\centering
\includegraphics [width=8.5cm]{1427f2.eps}\end{figure}](/articles/aas/full/1998/11/ds1427/Timg31.gif) |
Figure 2: Time stability of the laser pulse width. The time interval between two laser pulses is 0.2 s |
The return detector is an avalanche photodiode built by Silicon Sensor
(SSOAD230H) working in Geiger mode (Ekstrom 1981); (Samain 1998). Its aperture is ![]() m. The photodiode break-down
voltage is 140 V. The total voltage applied on the photodiode to detect
the photons is 290 V. The detector operates at
m. The photodiode break-down
voltage is 140 V. The total voltage applied on the photodiode to detect
the photons is 290 V. The detector operates at ![]() . The
quantum efficiency in Geiger mode is 0.2. Some workbench experiments have
shown that the transit time experiences a variation versus the position of
the light spot on the active surface of the detector. With r being the
distance between the photodiode centre and the spatial point where the
photon is absorbed, and
. The
quantum efficiency in Geiger mode is 0.2. Some workbench experiments have
shown that the transit time experiences a variation versus the position of
the light spot on the active surface of the detector. With r being the
distance between the photodiode centre and the spatial point where the
photon is absorbed, and ![]() the transit time difference
between the response obtained with a photon absorbed at the centre and the
response obtained at a distance r, we have measured
the transit time difference
between the response obtained with a photon absorbed at the centre and the
response obtained at a distance r, we have measured
| |
(2) |
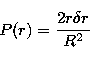 |
(3) |
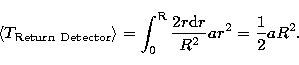 |
(4) |
The best time precision ![]() of the photodiode is
obtained with r=0 and with a spot radius R as small as possible. Then, we
have
of the photodiode is
obtained with r=0 and with a spot radius R as small as possible. Then, we
have ![]()
![]() ps. In the case
where the whole active area of the photodiode is used we have
ps. In the case
where the whole active area of the photodiode is used we have ![]() (r=0,R=115
(r=0,R=115 ![]() ps.
ps.
The size of the lunar return spot is determined by the optical configuration
and by the atmospheric turbulence. The seeing, which roughly varies from ![]() to
to ![]() , modifies the spot size from 50 to 200
, modifies the spot size from 50 to 200 ![]() m
and the return
detector precision
m
and the return
detector precision ![]() lies in an interval of
35-50 ps rms.
lies in an interval of
35-50 ps rms.
![\begin{figure}
\centering
\includegraphics [width=8.5cm]{1427f3.eps}\end{figure}](/articles/aas/full/1998/11/ds1427/Timg52.gif) |
Figure 3: Retroreflector orientation. The reflection point precision depends on the angle between n and Ot |
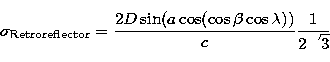 |
(5) |
| |
(6) |
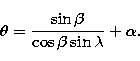 |
(7) |
![]() mm2 for Apollo XV
mm2 for Apollo XV
![]() mm2 for Apollo IX and XIV
mm2 for Apollo IX and XIV
![]() mm2 for Lunakhod 1 and 2
mm2 for Lunakhod 1 and 2
![]() lies in an interval from 0 to 350 ps rms for the
larger retroreflectors (Apollo XV), and from 0 to 150 ps for the smallest.
The correlation between the theoretical and the observed precisions on
Apollo versus the lunar libration XV will be studied in the following
(Sect. 4.2).
lies in an interval from 0 to 350 ps rms for the
larger retroreflectors (Apollo XV), and from 0 to 150 ps for the smallest.
The correlation between the theoretical and the observed precisions on
Apollo versus the lunar libration XV will be studied in the following
(Sect. 4.2).
Some noise events can degrade the precision of the measurements. These noise
events are introduced by photons coming from the Sun and by thermal
triggering of the avalanche photodiode. The latter events can be neglected.
When the retroreflector is in the lunar day, the measured noise frequency ![]() is of about 2 MHz. On the contrary, in the lunar night the noise
frequency is a few kHz. This noise depends on the field of view of the
optics, the spectral width of the interferential filter placed in front of
the detector, and the telescope aperture. The light events outside a
temporal gate
is of about 2 MHz. On the contrary, in the lunar night the noise
frequency is a few kHz. This noise depends on the field of view of the
optics, the spectral width of the interferential filter placed in front of
the detector, and the telescope aperture. The light events outside a
temporal gate ![]() are eliminated. The noise
event number accumulated during an observation period
are eliminated. The noise
event number accumulated during an observation period ![]() in this gate
in this gate
![]() is
is ![]() , where
, where ![]() is
the laser rate (10 Hz). The noise events being random, the residual
precision
is
the laser rate (10 Hz). The noise events being random, the residual
precision ![]() is given by
is given by
| |
(8) |
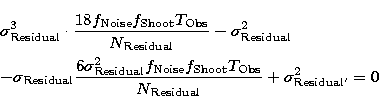 |
||
| (9) |
![\begin{figure}
\centering
\includegraphics [width=8.5cm]{1427f4.eps}\end{figure}](/articles/aas/full/1998/11/ds1427/Timg80.gif) |
Figure 4:
Precision degradation versus the quantity |
| |
(10) |
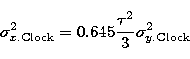 |
(11) |
The transit time sensitivity of the return detector versus the spatial
position of the light spot on the detector will introduce an error in the
distance measurement if the light spot of the calibration and the light spot
of the lunar returns are located at different places or, if the spot sizes
are different. The speed aberration, due to Earth and Moon rotation,
combined with an eventual non alignment of the laser axis with the reception
axis, can introduce an offset with regard to the centre of the photodiode of
the order of 100 ![]() m. This offset, expressed in time
versus Eq. (2), gives
m. This offset, expressed in time
versus Eq. (2), gives ![]() ps. A
gelatine polarizer is placed on
the calibration path to adjust the calibration level versus the telescope
orientation. This polarizer acts also as a diffuser and broadens the
calibration spot size which is then limited by the diaphragm. Combining the
optical aberration and this diaphragm limitation, the spot radius of the
calibration pulse is 100
ps. A
gelatine polarizer is placed on
the calibration path to adjust the calibration level versus the telescope
orientation. This polarizer acts also as a diffuser and broadens the
calibration spot size which is then limited by the diaphragm. Combining the
optical aberration and this diaphragm limitation, the spot radius of the
calibration pulse is 100 ![]() m, and
m, and ![]() for the calibration is 25 ps. This
magnification of the calibration spot size allows us to obtain a calibration
information which is quite independent of the adjustment of the calibration
spot position. As compared to
for the calibration is 25 ps. This
magnification of the calibration spot size allows us to obtain a calibration
information which is quite independent of the adjustment of the calibration
spot position. As compared to ![]() an error of 25 ps can be
introduced in the global error budget by this alignment problem. Another
accuracy problem will be encountered if the voltage mean value applied on
the return detector for the calibration echoes is different from the one
used for the lunar echoes. The observed voltage difference is of the order
of 3 V. Converted into time, this will introduce an error in the range of
15 ps. Finally, the phenomena introduced by the return detector degrade the
accuracy measurement with a term
an error of 25 ps can be
introduced in the global error budget by this alignment problem. Another
accuracy problem will be encountered if the voltage mean value applied on
the return detector for the calibration echoes is different from the one
used for the lunar echoes. The observed voltage difference is of the order
of 3 V. Converted into time, this will introduce an error in the range of
15 ps. Finally, the phenomena introduced by the return detector degrade the
accuracy measurement with a term ![]() = 65 ps.
= 65 ps.
The echoes detected from the Moon are corrected with the term ![]() . This mean value is computed from a set
of dates, recorded over a time
. This mean value is computed from a set
of dates, recorded over a time ![]() . The period
. The period ![]() should be deduced from the calibration time stability. The typical shape of
this time stability is shown in Fig. 6.
should be deduced from the calibration time stability. The typical shape of
this time stability is shown in Fig. 6.
![\begin{figure}
\centering
\includegraphics [width=8.5cm]{1427f6.eps}\end{figure}](/articles/aas/full/1998/11/ds1427/Timg96.gif) |
Figure 6:
LLR calibration time stability. Between |
It is essential to know the air index on the travel path of the laser beam
to take into account the delay introduced in the
measurements (Herring 1992). This delay is computed from the Marini Murray
model (Marini & Murray 1973). The computation uses some
atmospheric measurements performed near the station. An error in the
evaluation of the real air index value will introduce an accuracy problem.
The accuracy ![]() evaluated on the delay is 15 ps when the Moon
is observed at an elevation of 90
evaluated on the delay is 15 ps when the Moon
is observed at an elevation of 90![]() (that is not possible in
France) and 70 ps at 15
(that is not possible in
France) and 70 ps at 15![]() . An unknown air index variation on
the laser beam path will degrade the precision of the measurement. The short
term perturbation 0.5 <
. An unknown air index variation on
the laser beam path will degrade the precision of the measurement. The short
term perturbation 0.5 < ![]() < 1000 s of the residual is a white
phase noise (see Fig. 8). If the atmosphere has an effect on the
measurement, this effect has a time constant lower than 0.5 s or greater
than 1000 s. Some stellar interferometry experiments demonstrate that a
phase correlation exists between two beacons a few tens of meters apart. The
evolution of the phase between the beacons is a continuous function. The
phase drift is lower than 100 wavelengths over 100 s. The corresponding time
propagation difference between the beacons is then smaller than 0.1 ps. This
interferometric measurements are relative (between the beacons) and do not
give any information on the absolute time propagation of the light.
Nevertheless, it seems improbable that the atmosphere exhibits an important
air index variation at a spatial scale of a few tens of meters with a time
scale lower than 0.5 s. Concerning the air index fluctuation over a period
longer than 1000 s, Fig. 8 cannot yield any consistent information, since
the observed flicker noise could be generated by some other sources
(computation, clock, return detector, ...). Other experiments should be
performed to improve our knowledge of the long term atmosphere comportment.
In conclusion, the dispersion
< 1000 s of the residual is a white
phase noise (see Fig. 8). If the atmosphere has an effect on the
measurement, this effect has a time constant lower than 0.5 s or greater
than 1000 s. Some stellar interferometry experiments demonstrate that a
phase correlation exists between two beacons a few tens of meters apart. The
evolution of the phase between the beacons is a continuous function. The
phase drift is lower than 100 wavelengths over 100 s. The corresponding time
propagation difference between the beacons is then smaller than 0.1 ps. This
interferometric measurements are relative (between the beacons) and do not
give any information on the absolute time propagation of the light.
Nevertheless, it seems improbable that the atmosphere exhibits an important
air index variation at a spatial scale of a few tens of meters with a time
scale lower than 0.5 s. Concerning the air index fluctuation over a period
longer than 1000 s, Fig. 8 cannot yield any consistent information, since
the observed flicker noise could be generated by some other sources
(computation, clock, return detector, ...). Other experiments should be
performed to improve our knowledge of the long term atmosphere comportment.
In conclusion, the dispersion ![]() introduced by the
atmosphere, computed over a period lower than 1000 s, will be small as
compared to other dispersions and will be neglected in the global precision
error budget.
introduced by the
atmosphere, computed over a period lower than 1000 s, will be small as
compared to other dispersions and will be neglected in the global precision
error budget.
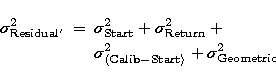 |
||
| (12) |
 |
||
| (13) |
- ![]() = 4 ps: leading edge variation of the laser
pulse
= 4 ps: leading edge variation of the laser
pulse
- ![]() = 30 ps: width of the light pulse
= 30 ps: width of the light pulse
- ![]() = 5 ps and
= 5 ps and
![]() = 50 ps: start and return detector
= 50 ps: start and return detector
- ![]() = 5 ps: electronic timer
= 5 ps: electronic timer
- ![]() = 10 ps: time stability of the clock
over a period of 2.5 s
= 10 ps: time stability of the clock
over a period of 2.5 s
- ![]() = 0 - 350 ps: retroreflector orientation
= 0 - 350 ps: retroreflector orientation
- ![]() = 4 ps: calibration.
= 4 ps: calibration.
Numerically, one gets: ![]() = 60 ps in the case
where the retroreflector dispersion is 0. This value corresponds to the
better precision obtainable on the travel time of light pulses from Earth to
Earth via the Moon. This time precision allows us to measure the Earth-Moon
distance with a precision of 9 mm. This computation agrees with the
calibration precision computed over
= 60 ps in the case
where the retroreflector dispersion is 0. This value corresponds to the
better precision obtainable on the travel time of light pulses from Earth to
Earth via the Moon. This time precision allows us to measure the Earth-Moon
distance with a precision of 9 mm. This computation agrees with the
calibration precision computed over ![]() . Among all the
instrumental error sources, the main dispersion comes from the return
detector.
. Among all the
instrumental error sources, the main dispersion comes from the return
detector.
![\begin{figure}
\centering
\includegraphics [width=8.5cm]{1427f7.eps}\end{figure}](/articles/aas/full/1998/11/ds1427/Timg113.gif) |
Figure 7: Residual precision computed from the corner cubes array orientation and the intrinsic LLR performances versus the residual precision measured. Retroreflector: Apollo XV |
- ![]() = 3 ps: frequency clock accuracy
= 3 ps: frequency clock accuracy
- ![]() = 10 ps: accuracy of the geometrical distance of the
calibration corner cube as compared to the reference point of the station
= 10 ps: accuracy of the geometrical distance of the
calibration corner cube as compared to the reference point of the station
- ![]() = 65 ps: accuracy of the return detector for
the calibration
= 65 ps: accuracy of the return detector for
the calibration
- ![]() = 50 ps: accuracy evaluation of the atmospheric delay
= 50 ps: accuracy evaluation of the atmospheric delay
- ![]()
![]() = 220-1200 ps: residual precision 65 <
= 220-1200 ps: residual precision 65 < ![]() < 350 ps.
< 350 ps.
One gets
 |
||
| (14) |
Numerically, one obtains, in the best libration condition, ![]() ps, which corresponds to a Earth-Moon distance accuracy
equal to 50 mm. The quantity
ps, which corresponds to a Earth-Moon distance accuracy
equal to 50 mm. The quantity ![]() /2 is an evaluation of the absolute
value of the maximum difference between the round trip time deduced from one
echo and the real distance. It illustrates the worst possible case to
envisage. As we will see in the following chapter, the measurement accuracy
can be improved by eliminating a fraction of the noise introduced by the
residual precision. This is achieved by computing the mean value of many
individual measurements.
/2 is an evaluation of the absolute
value of the maximum difference between the round trip time deduced from one
echo and the real distance. It illustrates the worst possible case to
envisage. As we will see in the following chapter, the measurement accuracy
can be improved by eliminating a fraction of the noise introduced by the
residual precision. This is achieved by computing the mean value of many
individual measurements.
| |
(15) |
![\begin{figure}
\centering
\includegraphics [width=8.5cm,clip]{1427f8.eps}\end{figure}](/articles/aas/full/1998/11/ds1427/Timg127.gif) |
Figure 8:
Residual time stability computed from echoes obtained on
Apollo XV. The normal point precision deduced from the 23/09/96 observation
session is 10 ps (1.5 mm), and the best |
- 10 < ![]() < 1500 s:
< 1500 s: ![]() corresponding to a white phase noise
corresponding to a white phase noise
- 1500 < ![]() < 5000 s:
< 5000 s: ![]() corresponding to a flicker phase noise.
corresponding to a flicker phase noise.
In this case, the best choice for ![]() is 1500 s. The
precision of the normal point computed over this period is
is 1500 s. The
precision of the normal point computed over this period is ![]() ps which corresponds to a
distance precision equal to 1.5 mm. The accuracy of the normal point is
improved as compared to the accuracy of each individual echo. One gets
ps which corresponds to a
distance precision equal to 1.5 mm. The accuracy of the normal point is
improved as compared to the accuracy of each individual echo. One gets
 |
||
| (16) |
In practice, the period ![]() is not a constant. This way, to
preserve all the information in the normal point, a time stability analysis
is necessary. Another way is to set
is not a constant. This way, to
preserve all the information in the normal point, a time stability analysis
is necessary. Another way is to set ![]() small enough so to be
sure that no information has been eliminated. In this case, both the
computational time and the amount of data will be raised. Furthermore, the
accuracy and the precision of the normal point will not illustrate the best
accuracy and precision available. In all cases, since information storage is
today not a problem, the echoes should be saved without any filtering (one
year of LLR echoes would represent only a few Mo).
small enough so to be
sure that no information has been eliminated. In this case, both the
computational time and the amount of data will be raised. Furthermore, the
accuracy and the precision of the normal point will not illustrate the best
accuracy and precision available. In all cases, since information storage is
today not a problem, the echoes should be saved without any filtering (one
year of LLR echoes would represent only a few Mo).
Copyright The European Southern Observatory (ESO)