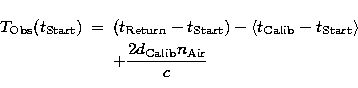Up: Millimetric Lunar Laser Ranging
The experiment, as performed at OCA, is shown in Fig. 1.
![\begin{figure}
\centering
\includegraphics [width=8.5cm]{1427f1.eps}\end{figure}](/articles/aas/full/1998/11/ds1427/Timg10.gif) |
Figure 1:
OCA Lunar Laser Ranging facility |
The YAG laser
emits four short pulses at a rate of 10 Hz. The time intervals between the
first and the second pulse, the third and the last one, are respectively:
1.6 ns, 4.1 ns and 5.7 ns. This temporal code, imagined by Jean-François
Mangin, permits to deduce, without any ambiguity, the pulse position in the
echo diagram. A telescope of 1.5 meter aperture collimates the laser beam in
the lunar direction. A fraction of the photons coming from the laser output
is sent onto a PIN photodiode. This detector is connected to a start timer
giving the start time  of the laser pulse. The photons coming
from the Moon impinge a return detector. This return detector is connected
to a return timer, similar to the start timer, giving
of the laser pulse. The photons coming
from the Moon impinge a return detector. This return detector is connected
to a return timer, similar to the start timer, giving 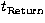 . The time
base of the timers is a caesium atomic clock. A corner cube, at the
telescope output, returns a fraction of the emitted photons onto the return
detector (Mangin 1982). This permits to calibrate the
instrumentation. The arrival time of the calibration pulse on the return
detector is
. The time
base of the timers is a caesium atomic clock. A corner cube, at the
telescope output, returns a fraction of the emitted photons onto the return
detector (Mangin 1982). This permits to calibrate the
instrumentation. The arrival time of the calibration pulse on the return
detector is  . This calibration information allows us to know
accurately the transit time of the light pulse between the corner cube on
the Moon and the calibration corner cube. The spatial reference of the LLR
station is the crossing of the telescope mount axes. Finally, the distance
between this spatial reference and the target will be known if the distance
between the cross axis and the calibration corner cube distance
. This calibration information allows us to know
accurately the transit time of the light pulse between the corner cube on
the Moon and the calibration corner cube. The spatial reference of the LLR
station is the crossing of the telescope mount axes. Finally, the distance
between this spatial reference and the target will be known if the distance
between the cross axis and the calibration corner cube distance  is known (see Fig. 1). This distance is measured geometrically. The round
trip travel time
is known (see Fig. 1). This distance is measured geometrically. The round
trip travel time 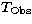 of the light pulse between the spatial reference
and the Moon corner cubes is
of the light pulse between the spatial reference
and the Moon corner cubes is
| 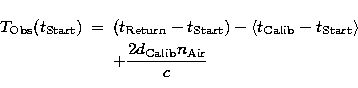 |
|
| (1) |
where 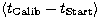 is the calibration
mean value integrated over a period
is the calibration
mean value integrated over a period  ,
,  is the air
refraction index, and c is the light velocity. The mean value of the photon
number coming from the Moon and detected per pulse by the return detector is
of the order of 0.01. Thus, the return detector works in a single photon
mode. Since the transit time of the return detection device depends on the
number of received photons, the calibration will be valid if it is also
performed in a single photon mode.
is the air
refraction index, and c is the light velocity. The mean value of the photon
number coming from the Moon and detected per pulse by the return detector is
of the order of 0.01. Thus, the return detector works in a single photon
mode. Since the transit time of the return detection device depends on the
number of received photons, the calibration will be valid if it is also
performed in a single photon mode.


Up: Millimetric Lunar Laser Ranging
Copyright The European Southern Observatory (ESO)
![\begin{figure}
\centering
\includegraphics [width=8.5cm]{1427f1.eps}\end{figure}](/articles/aas/full/1998/11/ds1427/Timg10.gif)