

Up: Abundances in metal-rich
If we assume that the true continuum level is not wildly different
from the fitted continuum the error in measured equivalent width can
at the most be as large, in difficult cases, as 2 mÅ for weak
lines, i.e.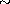 20%, and 4-5 mÅ for stronger lines, i.e.
20%, and 4-5 mÅ for stronger lines, i.e.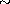 10%. This translates to typically 0.08 dex in the resulting abundance
derived from a line of strength 10 mÅ and 0.04 dex for a line of
strength
10%. This translates to typically 0.08 dex in the resulting abundance
derived from a line of strength 10 mÅ and 0.04 dex for a line of
strength
50 mÅ. Apart from the effects of the
continuum errors and blends, the error
in derived abundances due to errors in the measurement of the
equivalent width of a line is negligible (< 0.01 dex). In general, the
lines and continua are, due to the high S/N and high resolution, easy to
fit and the errors given above should be regarded as upper limits.
The oscillator strengths, derived from the observed solar spectrum,
can be affected by misidentification, by undetected blends and by
errors in continuum fitting and measurements of equivalent widths in
the solar spectrum. As in the stellar spectra, location of the continuum is
a much larger source of error than the actual measurement of a
line. (Note, however, that the solar spectra have higher S/N, usually
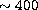 , and thus, identification of the continuum becomes easier
as well as identification of lines. The Sun is also more metal-poor
than the programme stars, which makes identification of the continuum
in the Sun easier.) Using the results in Sect. 5.1 (click here) we find
that errors in
, and thus, identification of the continuum becomes easier
as well as identification of lines. The Sun is also more metal-poor
than the programme stars, which makes identification of the continuum
in the Sun easier.) Using the results in Sect. 5.1 (click here) we find
that errors in 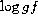 -values may be as large as 0.08 dex, but
a more characteristic number is 0.04 dex.
-values may be as large as 0.08 dex, but
a more characteristic number is 0.04 dex.
Since we perform a purely differential analysis errors due to misplaced
continua, neglected blends, etc.
should partly cancel in the first approximation and not affect the
resulting differential abundances very much, as long as we study stars
similar to the Sun.
In the selection of lines we have carefully avoided all lines that
could be subject to blending with nearby lines as given in
Moore et al. (1966). For ions with several lines measured we have also looked
for lines which produces abnormally high abundances as compared with
the majority of the lines. This led us to exclude three
FeII lines from our final analyses: 6383.71, 6383.45, and
6627.32 Å.
Edvardsson et al. (1993a) estimate the error in the effective temperature
due to errors in b - y to range from
-50 K to +100 K and the
corresponding error in 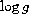 to be
to be 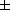 0.2 dex.
0.2 dex.
The effects of such errors in 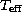 and
and 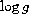 are exemplified
in Table 3 (click here). As expected, abundances derived from
ions are most sensitive to changes in surface gravity while abundances
derived from atoms are most sensitive to changes in effective
temperature. In general, errors in derived abundances are smaller
than 0.10 dex for atoms when varying the effective temperature by
are exemplified
in Table 3 (click here). As expected, abundances derived from
ions are most sensitive to changes in surface gravity while abundances
derived from atoms are most sensitive to changes in effective
temperature. In general, errors in derived abundances are smaller
than 0.10 dex for atoms when varying the effective temperature by 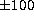 K and less than 0.02 dex when the surface gravity is varied by
K and less than 0.02 dex when the surface gravity is varied by
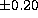 dex; they are smaller than 0.02 dex for ions when the
effective temperature is varied and less than 0.10 dex when the
surface gravity is varied.
dex; they are smaller than 0.02 dex for ions when the
effective temperature is varied and less than 0.10 dex when the
surface gravity is varied.
ID / 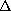 | [OI] | NaI | MgI | AlI | SI | CaI | TiI | Cr I | CrII | FeI | FeII | NiI | EuII | | |
|
HD 72946 | 0.16 | 0.22 | 0.24 | 0.23 | 0.13 | 0.22 | 0.38 | 0.24 | 0.09 | 0.24 | 0.00 | 0.18 | 0.09 | | |
|
+100 K | +0.01 | +0.04 | +0.04 | +0.06 | +0.01 | +0.06 | +0.08 | +0.06 | -0.03 | +0.05 | +0.01 | +0.05 | 0.00 | | |
|
+0.2 dex | +0.09 | -0.03 | -0.01 | -0.01 | -0.01 | -0.02 | 0.00 | 0.00 | +0.08 | -0.01 | +0.12 | +0.01 | +0.08 | | |
|
HD 103932 | 0.28 | | 0.30 | 0.14 | 0.27 | -0.12 | +0.03 | 0.01 | 0.44 | 0.14 | 0.57 | 0.41 | 0.32 | | |
|
+200 K | +0.05 | | -0.08 | +0.12 | -0.18 | +0.18 | +0.24 | +0.12 | -0.18 | -0.04 | -0.32 | -0.05 | -0.01 | | |
|
+0.4 dex | +0.16 | | +0.02 | -0.04 | +0.10 | -0.04 | -0.02 | +0.02 | +0.19 | +0.07 | +0.21 | +0.09 | +0.15 | | |
|
HD 110010 | -0.04 | 0.53 | 0.48 | 0.40 | 0.51 | 0.35 | 0.29 | 0.30 | 0.22 | 0.35 | 0.33 | 0.31 | 0.16 | | |
|
+100 K | +0.01 | +0.05 | +0.04 | +0.04 | +0.01 | +0.06 | +0.08 | +0.06 | +0.03 | +0.06 | -0.05 | +0.05 | 0.00 | | |
|
+0.2 dex | +0.09 | -0.02 | -0.01 | -0.02 | -0.01 | -0.01 | 0.00 | 0.00 | +0.08 | -0.01 | -0.03 | 0.00 | +0.09 | | |
| | | | | | | | | | | | | | | | |
Table 3: Effects on abundance estimates for a number of elements
from changes in fundamental parameters of the model atmosphere. The
resulting abundances are shown for 3 stars: HD 72946 (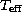 /
/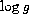 /[Fe/H]) = (5911/4.4/0.24), HD 103932
(4510/4.58/0.16), and HD 110010 (5965/4.08/0.35). The first line for
each star gives [X/H], X being the ion indicated in the header, derived using a model
atmosphere constructed with the stellar parameters adopted in this
study. The following lines contain the differences when effective
temperature or surface gravity has been changed as indicated in the
first column. Note that the changes in parameters are different, and
larger, for HD 103932
/[Fe/H]) = (5911/4.4/0.24), HD 103932
(4510/4.58/0.16), and HD 110010 (5965/4.08/0.35). The first line for
each star gives [X/H], X being the ion indicated in the header, derived using a model
atmosphere constructed with the stellar parameters adopted in this
study. The following lines contain the differences when effective
temperature or surface gravity has been changed as indicated in the
first column. Note that the changes in parameters are different, and
larger, for HD 103932
For dwarf stars that are significantly more metal-rich than the Sun
(e.g. [Me/H]  0.2 dex), the
metallicity used in the calculation of the model atmosphere is
important, since it governs the line blanketing and thus the
temperature structure of the model atmosphere. We may expect that
final derived abundances are sensitive to this parameter. Following
Edvardsson et al. (1993a) we decreased (and in a few cases increased) the
metallicities to the values derived for [Fe/H] in a preliminary
abundance analysis and reiterated the abundance determination. (We
have determined iron abundances from lines arising from both FeI and
FeII. For FeI usually more than 30 lines were analysed and
for FeII three to four lines. The formal error in the mean [Fe/H]
derived from FeI for a certain star is usually smaller than 0.02 dex.)
In the mean we find that we had to reduce the abundances by 0.07 dex
from the initial photometric values, with a spread of 0.01 dex, Table
1 (click here). Apparently, our photometric metallicities tend to
overestimate the metal content in these metal-rich stars as compared
to the iron abundance derived from spectral abundance analysis,
Fig. 2 (click here).
0.2 dex), the
metallicity used in the calculation of the model atmosphere is
important, since it governs the line blanketing and thus the
temperature structure of the model atmosphere. We may expect that
final derived abundances are sensitive to this parameter. Following
Edvardsson et al. (1993a) we decreased (and in a few cases increased) the
metallicities to the values derived for [Fe/H] in a preliminary
abundance analysis and reiterated the abundance determination. (We
have determined iron abundances from lines arising from both FeI and
FeII. For FeI usually more than 30 lines were analysed and
for FeII three to four lines. The formal error in the mean [Fe/H]
derived from FeI for a certain star is usually smaller than 0.02 dex.)
In the mean we find that we had to reduce the abundances by 0.07 dex
from the initial photometric values, with a spread of 0.01 dex, Table
1 (click here). Apparently, our photometric metallicities tend to
overestimate the metal content in these metal-rich stars as compared
to the iron abundance derived from spectral abundance analysis,
Fig. 2 (click here).
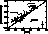
Figure 2: Metallicities determined from photometry vs. iron abundances
derived in our spectral analysis. The one-to-one relation is
indicated by a dotted line and a least-square fit to the data points,
taking the error in [Fe/H] to be 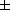 0.02 and the error in the
photometric metallicities to be
0.02 and the error in the
photometric metallicities to be 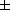 0.1, is also shown, dashed
line. The
0.1, is also shown, dashed
line. The 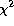 -proabability
for this fit is 0.92. A fit made without taking the errors into account
is shown by a long-dashed line. The stars from Barbuy & Grenon (1990),
-proabability
for this fit is 0.92. A fit made without taking the errors into account
is shown by a long-dashed line. The stars from Barbuy & Grenon (1990),
 , and HD 171999A and HD 175518, denoted by
, and HD 171999A and HD 175518, denoted by  symbols,
were excluded from the fit (see Sect. 5.5 (click here))
symbols,
were excluded from the fit (see Sect. 5.5 (click here))
Usually, the differences between the metallicities estimated from
photometry, are close enough to those derived from spectroscopy that
we have not found it necessary to reiterate the determination of
effective temperature and 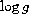 . (The determination of metallicity
was, however, changed according to the spectroscopic result so that
the final model used in the analysis had [Me/H] consistent with the
resulting spectroscopic [Fe/H].) However, for some of the stars the
photometry indicates rather extreme metallicities compared with the
spectroscopic iron abundances. For HD 171999A we have only measured 6
FeI equivalent widths (since this star was only observed with
one CCD setting, see Sect. 3.1 (click here)) and thus the
spectroscopically determined iron abundance is not as good as for the
other stars. However, we note that the line-to-line scatter is small,
0.03 dex. For HD 175518 it is questionable if its photometric
metallicity is realistic. In any large catalogue there will always be
a few stars with
. (The determination of metallicity
was, however, changed according to the spectroscopic result so that
the final model used in the analysis had [Me/H] consistent with the
resulting spectroscopic [Fe/H].) However, for some of the stars the
photometry indicates rather extreme metallicities compared with the
spectroscopic iron abundances. For HD 171999A we have only measured 6
FeI equivalent widths (since this star was only observed with
one CCD setting, see Sect. 3.1 (click here)) and thus the
spectroscopically determined iron abundance is not as good as for the
other stars. However, we note that the line-to-line scatter is small,
0.03 dex. For HD 175518 it is questionable if its photometric
metallicity is realistic. In any large catalogue there will always be
a few stars with 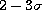 errors in the photometry. Since
spectroscopic iron abundances indicate a much lower metallicity this
is most probably an example of that.
errors in the photometry. Since
spectroscopic iron abundances indicate a much lower metallicity this
is most probably an example of that.
We have studied, for HD 175518, the effects on derived abundances if
[Me/H] is lowered to 0.2 dex as indicated by the spectroscopy, thus
affecting the estimates of the rest of the fundamental parameters.
The lower metallicity implies a lower effective temperature; [Me/H] =
0.22 dex corresponds to a decrease of 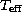 by
by 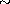 200 K.
From Table 3 (click here) we see that most elements will change
by
200 K.
From Table 3 (click here) we see that most elements will change
by 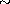 0.1 dex and thus the star will mainly move horizontally, by
0.1 dex and thus the star will mainly move horizontally, by
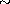 0.1 dex, in our relative abundance diagrams. HD 175518 is an
extreme case in our sample and the abundances of the other stars and
general abundance trends for the whole sample should not be affected
by comparable amounts.
0.1 dex, in our relative abundance diagrams. HD 175518 is an
extreme case in our sample and the abundances of the other stars and
general abundance trends for the whole sample should not be affected
by comparable amounts.
Some of the elements analysed are well known to be subject to
hyperfine structure. We have not taken this into account when deriving
the chemical abundances. Instead, for those elements in particular we
have aimed at selecting weak enough lines, so that the neglect of
hyperfine structure in the abundance analysis should not affect the
calculated equivalent widths and thus not the derived abundances.
Figure 3 (click here) shows copper abundances derived from the two lines
used in our study as functions of equivalent width. Our data clearly
show that the stronger copper line is
subject to hyperfine structure and that these lines
should be analysed using synthetic spectroscopy taking the hyperfine
structure splitting into account. Results by Summers (1994) may
suggest departures from LTE in the population of levels in the copper
atom. We do not, however, have enough data to make further empirical
investigations of such departures from LTE. We omit copper
abundances from the following discussion.

Figure 3: Copper abundances derived from the lines at
5220 Å,  symbols, and 7933 Å,
symbols, and 7933 Å,  symbols.
The widths of these
lines are 16 and 36 mÅ, respectively,
in the solar flux spectrum
symbols.
The widths of these
lines are 16 and 36 mÅ, respectively,
in the solar flux spectrum
The manganese and cobalt lines used in this study are not
saturated. When plotting abundances derived from each line as a
function of equivalent width no distinct pattern was found; indicating
that the omission of hyperfine structure in the treatment of the lines
is not problematic. In many stars lines with equivalent widths of
about 20 and 60 mÅ, respectively, gave manganese abundances that
are in excellent mutual agreement.
The lines used to derive abundances for the heavy s- and r-process
elements are sufficiently weak in our programme stars to be safely used
as abundance criteria in spite of being subject to hyperfine
structure. Among the light s-process elements we note, however, that only YII, and maybe YI, have lines strong enough and secure enough
that derived abundances can be used with confidence. The 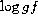 -values
for zirconium are very uncertain because of the faintness of the lines
in the Sun.
-values
for zirconium are very uncertain because of the faintness of the lines
in the Sun.
Deviations from the Boltzmann excitation equilibrium, which might
suggest an error in the effective temperature, can be traced by
studying abundances derived from individual lines as a function of the
lower excitation potential for the lines. 32 FeI lines
measured in most of the stars, marked in Table 2 (click here), were
selected for this purpose. For all stars (excluding four stars with
too few lines observed) the abundance of each iron line was plotted
as a function of the excitation energy of the lower level,
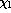 , and a least square linear fit was made to the points of
the form [Fe/H]=
, and a least square linear fit was made to the points of
the form [Fe/H]= 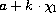 , Fig. 4 (click here). The mean
value of the slope coefficients, k, is 0.00 (excluding the K dwarf
stars), suggesting that the systematic errors in effective
temperatures are small.
, Fig. 4 (click here). The mean
value of the slope coefficients, k, is 0.00 (excluding the K dwarf
stars), suggesting that the systematic errors in effective
temperatures are small.

Figure 4: Two examples of how the slope coefficients in
Fig. 5 (click here) were obtained. Examples are for a) HD 91204
and b) HD 125968. The dashed lines represent linear least-square
linear fits
Next, these linear coefficients were plotted as functions of effective
temperature, surface gravity and spectroscopically derived iron
abundance, Fig. 5 (click here). We have compared our results with
those obtained by Edvardsson et al. (1993a) (their Figs. 9a-f) and find that
the two studies span the same range of excitation energy slopes,
k. There are small but systematic deviations from the excitation
equilibrium, varying with effective temperature. A change in 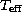 of +100 K results in a
of +100 K results in a 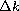 of +0.006 dex eV-1. The
change of excitation energy slope with surface gravity estimates seems to
reflect the variation of surface
gravity with effective temperature (surface gravity
increases as effective temperature decreases).
of +0.006 dex eV-1. The
change of excitation energy slope with surface gravity estimates seems to
reflect the variation of surface
gravity with effective temperature (surface gravity
increases as effective temperature decreases).
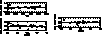
Figure 5: The slope coefficients from the
excitation energy balance diagram for each star plotted vs. effective
temperature, surface gravity and spectroscopically derived iron
abundances. The star with the lowest k is
HD 180890. Linear least square fits yield: a) 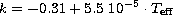 , b)
, b) 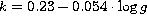 , c)
, c) 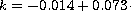 [Fe/H]
[Fe/H]
In many studies surface gravities are determined by requiring
ionization equilibrium. This is typically made by changing the surface
gravity until the iron abundances derived from FeI and
FeII lines yield the same abundance. We have not, as discussed
earlier, used this method. As we will see this has led us to discover
what appears to be a case of significant overionization in K dwarf
stars and an opposite smaller effect for the hotter stars (see
Fig. 7 (click here)).
What would the effects be if we assumed ionization equilibrium, and
adjusted the surface gravities accordingly? We can estimate changes
in the stellar abundances from the results of Table
3 (click here) and Table 11 (click here). From this we find that
half of the stars should have their surface gravities increased by
0.25 - 0.35 dex to achieve ionization equilibrium for iron. This
means that the the iron abundance will change with 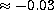 . Abundances of other elements will change with similar amounts
but with differing signs, which means that for some elements [X/Fe]
will change by up to 0.1 dex and for others not at all. However, we
note that the oxygen abundances are very sensitive to the surface
gravity and may change by up to 0.2 dex. As a comparison we estimate
the maximum error in the derived oxygen abundance caused by
incorrectly set continua to be less than 0.1 dex.
. Abundances of other elements will change with similar amounts
but with differing signs, which means that for some elements [X/Fe]
will change by up to 0.1 dex and for others not at all. However, we
note that the oxygen abundances are very sensitive to the surface
gravity and may change by up to 0.2 dex. As a comparison we estimate
the maximum error in the derived oxygen abundance caused by
incorrectly set continua to be less than 0.1 dex.
An adjustment downwards of the gravities by about 0.3 dex would increase the
conflict with the gravity estimates from the CaI 6162 Å line
wings. We consider such a revision less probable.
Our results admit a comparison for five elements (scandium, vanadium,
chromium, iron and yttrium) of abundances derived from ions to
abundances derived from the corresponding atom, as function of
effective temperature, within a rather wide range of effective
temperature.
We find an apparent overionization as compared to expectations from
LTE calculations for the five K dwarf stars in our study,
Fig. 7 (click here). Our results are at first sight unexpected,
especially for the two K dwarf stars with iron abundances of 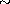 0.3 dex relative to the solar iron abundance, as derived from
FeI lines. In stars more metal-rich than the Sun the
photoionizing non-local UV-flux is more efficiently blocked than in
more metal-poor stars. However, as discussed in Sect. 5.9 (click here), the
stronger blocking may be more than compensated by the increased
temperature gradient which may enhance the non-locality of the
radiation field.
0.3 dex relative to the solar iron abundance, as derived from
FeI lines. In stars more metal-rich than the Sun the
photoionizing non-local UV-flux is more efficiently blocked than in
more metal-poor stars. However, as discussed in Sect. 5.9 (click here), the
stronger blocking may be more than compensated by the increased
temperature gradient which may enhance the non-locality of the
radiation field.
We have carefully inspected the CrII and FeII lines
in the K dwarf spectra and excluded all lines which may be
subject to severe blends in these cool stars. For FeII we used
the lines at 6456.39 and 6516.39 Å and for CrII the
lines at 5305.86 and 5310.69 Å. In spite of using blend
free lines the apparent overionization remains. The internal
consistency between abundances derived from the two FeII lines is
very good and this is also the case for CrII.
For scandium, vanadium and
yttrium blends remain a possible source of error, but the
similarity with the trends for iron and chromium suggests a
common cause of the apparent overionization for all these elements.
The iron abundances derived from the atom show no obvious trend with
effective temperature, see Fig. 6 (click here).

Figure 6: Iron abundances, derived in this study, as a
function of effective temperatures
A probable reason for these effects is overionization (see Sect.
5.9 (click here)). Before discussing this, however, we shall
explore the possibility that errors in
the temperature scale could also contribute significantly.
The calibration of the photometry in Olsen (1984) is, for 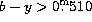 , based on a sample of 15 K and M dwarf stars using
stellar parameters from Cayrel de Strobel & Bentolila (1983).
The K
and M dwarf stars in Olsen's sample span a small range in
, based on a sample of 15 K and M dwarf stars using
stellar parameters from Cayrel de Strobel & Bentolila (1983).
The K
and M dwarf stars in Olsen's sample span a small range in 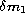 and
and 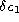 . This is reflected in the change in the calibration
at
. This is reflected in the change in the calibration
at 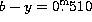 . For
. For 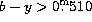 the calibration
is degenerate in metallicity. Olsen (1984) quotes an error of
the calibration
is degenerate in metallicity. Olsen (1984) quotes an error of
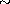 100 K for the effective temperature as derived from b-y.
100 K for the effective temperature as derived from b-y.
Additional photometry is scarce for our K dwarf stars. However, UBV
photometry exists and we have checked our effective temperatures using
the calibration of B-V by Johnson (1966), Table
4 (click here). These effective temperatures agree well with those
obtained from 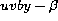 photometry. We note, however, that the
increased blocking for metal-rich stars, as compared to the
calibration stars used by Johnson (1966), may cause the present effective
temperatures to be underestimated. We have also derived (crude)
effective temperatures from calibrations of the MK classification.
Comparing the effective temperatures derived from photometry with
calibrations of effective temperatures as functions of spectral
classification (Bell & Gustafsson 1989 and Johnson 1966) we estimate
photometry. We note, however, that the
increased blocking for metal-rich stars, as compared to the
calibration stars used by Johnson (1966), may cause the present effective
temperatures to be underestimated. We have also derived (crude)
effective temperatures from calibrations of the MK classification.
Comparing the effective temperatures derived from photometry with
calibrations of effective temperatures as functions of spectral
classification (Bell & Gustafsson 1989 and Johnson 1966) we estimate
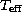 -values that deviate as compared with our standard
values as indicated in Table 4 (click here), Cols. 4 and 5.
-values that deviate as compared with our standard
values as indicated in Table 4 (click here), Cols. 4 and 5.
We have searched the literature for independent derivations of the
effective temperature for these stars. Those found agree well with
the photometric results, Table 4 (click here). As described earlier
we have also used the excitation energy balance to check our effective
temperatures. A change in effective temperature of +200 K for HD 32147
changed the slope of the least-square fit to the data points in the
diagram abundance-versus-excitation energy from +0.04 to +0.00. A
change of -200 K brought about a similar change but in the opposite
direction. Thus, the excitation equilibrium indicates that +200 K is
an acceptable change of the effective temperature for this star. The
line-to-line scatter in derived abundances from FeI lines for this
star is among the largest, 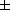 0.13. The same changes in effective
temperatures give similar values for HD 61606A. Since the other three K
dwarf stars are in the same effective temperature range and have
similar surface gravities as the two stars discussed here, and since
HD 32147 is the most metal-rich and HD 61606A is the most metal-poor of
the five K dwarf stars, changes in the fundamental parameters of the
remaining three stars will produce similar changes in abundances.
0.13. The same changes in effective
temperatures give similar values for HD 61606A. Since the other three K
dwarf stars are in the same effective temperature range and have
similar surface gravities as the two stars discussed here, and since
HD 32147 is the most metal-rich and HD 61606A is the most metal-poor of
the five K dwarf stars, changes in the fundamental parameters of the
remaining three stars will produce similar changes in abundances.
Table 4: The table shows results of different
derivations of the effective temperatures for the five
K dwarf stars; in the second column
as derived from the calibration by
Olsen (1984), and which are used in this study; in the third
spectral classes; in the fourth and fifth differences between
effective temperature derived in this work and from MK class
calibrations by Bell & Gustafsson (1989) and Johnson (1966);
in the sixth and
seventh B-V and effective temperatures derived from B-V using the
calibration of Johnson (1966). The three last columns
contain effective temperatures derived by other authors,
Neff et al. (1995), Morell (1994) and
Arribas & Martinez Roger (1989)
To conclude, a change in effective temperature of +200 to +400 K may
be allowed as judged from the excitation equilibrium. As is obvious
from Fig. 7 (click here), a change of this order of magnitude would
restore the LTE ionization balance for iron and chromium. The large
line-to-line scatter in derived abundances for lines with high
excitation energies makes attempts to derive effective temperatures
from excitation equilibria very dependent on one or two points in the
lower end of the excitation energy range, spanned by the lines as
illustrated in Fig. 4 (click here). Effective temperatures derived in
other studies and from B-V colours deviate by less than this from
our values.
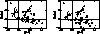
Figure 7: Abundance ratios of chromium and iron as functions of
[Fe/H]. [CrII/CrI], denotes [Cr/H]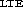 as
determined from CrII lines minus [Cr/H]
as
determined from CrII lines minus [Cr/H]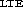 as
determined from CrI lines, and similarly for iron. Results for
chromium are shown in panel a) and for iron in panel
b)
as
determined from CrI lines, and similarly for iron. Results for
chromium are shown in panel a) and for iron in panel
b)  symbols denote the K dwarf stars and
symbols denote the K dwarf stars and  symbols
denote the stars from Barbuy & Grenon (1990). We exemplify, with
HD 61606A (
symbols
denote the stars from Barbuy & Grenon (1990). We exemplify, with
HD 61606A (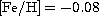 )and HD 103932 (
)and HD 103932 (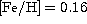 ),
how the resulting loci of the K dwarf stars will be shifted in the
diagram if the parameters of the stellar model atmospheres are
changed; changes of
),
how the resulting loci of the K dwarf stars will be shifted in the
diagram if the parameters of the stellar model atmospheres are
changed; changes of 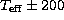 K (solid lines),
K (solid lines), 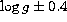 dex (dashed lines) and [Fe/H]
dex (dashed lines) and [Fe/H] 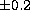 dex (dotted lines) are
shown. Filled triangles denote increased values of the respective
parameters while filled squares denote decreased values
dex (dotted lines) are
shown. Filled triangles denote increased values of the respective
parameters while filled squares denote decreased values
As already noted the surface gravities for the K dwarf stars seem
rather well determined, see Table 1 (click here). We also note that
our 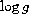 value for HD 131977A agrees well with that given by
Morell (1994). We conclude that realistic errors in
value for HD 131977A agrees well with that given by
Morell (1994). We conclude that realistic errors in 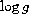 are
not enough to account for the departure from ionization equilibrium.
are
not enough to account for the departure from ionization equilibrium.
To conclude, we cannot from our analysis exclude that the
apparent pattern of overionization, at least partially, is due to
a temperature scale that is several hundred K too low. However, our
analysis, together with evidence from other studies, suggest that
deviations from LTE is a more plausible cause for the effects.
No detailed study has been devoted to the non-LTE effects on abundance
determinations for metal-rich dwarf stars, cooler than the Sun. A general
result of the available studies for solar-type stars is, however,
that several different effects are at play and may counteract each
other, and this makes all extrapolation to the present study of
metal-rich dwarf stars from studies of other types of stars or studies of
other elements questionable.
Among the significant effects are (cf. Bruls et al. 1992) resonance
line scattering, photon suction, ultraviolet overionization,
(infra)red over-recombination and optical line pumping. The
resonance-line scattering effects, in which photon losses cause the
source functions of resonance lines to drop far below the Planck
function at depths greater than those where the line optical depth is
unity, may lead to severe overestimates of abundances - e.g.,
Carlsson et al. (1994) find that in Li-rich cool stars the Li
abundance may well be overestimated by a factor of 3 as a result of
this.
Photon suction may, for metal-rich cases in particular, lead to
overpopulation of, e.g., the ground state and thus inhibit the effects
of overionization. This is the result of a compensation of photon
losses in the upper photosphere in resonance lines, as well as in
connected ladders of transitions, by a downward population
replenishment flow from the continuum reservoir. It is of great
significance for atoms with a majority of corresponding ions and with
pronounced cascade ladders. For complex atoms it should be of greatest
significance for the high-lying levels that thus can compensate
population depletion processes at lower excitation energy, e.g. caused
by overionization.
The ultraviolet overionization has been a major worry in analyses of
late type stellar spectra for two decades. It arises because the mean
intensity 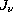 drops below the Planck function
drops below the Planck function 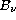 in the
line-forming regions of the atmosphere on the blue side of the
spectrum peak. Overionization is known to occur for FeI in the
Sun from levels a few electron volts below the continuum (see Rutten
1988 and references therein) and may more or less effect other metals
as well (see, e.g., Baumueller & Gehren 1996; Bruls 1993).
Overionization was suggested by Auman & Woodrow (1975) to be
significant for a number of elements with lower ionization energies in
cool stars. Major problems in modeling it are, however, the
difficulties in predicting the ultraviolet flux of late-type stars
with the crowding of spectral lines and the possible existence of an
"unknown opacity'' (cf., e.g. Gustafsson 1995), as well as the
dependence of the results of the notoriously uncertain collision cross
sections, e.g. for collisions with H atoms (cf. Steenbock & Holweger
1984). Empirically, #M&Mäckle et al. (1975) and
Ruland et al. (1980),
found a tendency for the low-excitation lines (
in the
line-forming regions of the atmosphere on the blue side of the
spectrum peak. Overionization is known to occur for FeI in the
Sun from levels a few electron volts below the continuum (see Rutten
1988 and references therein) and may more or less effect other metals
as well (see, e.g., Baumueller & Gehren 1996; Bruls 1993).
Overionization was suggested by Auman & Woodrow (1975) to be
significant for a number of elements with lower ionization energies in
cool stars. Major problems in modeling it are, however, the
difficulties in predicting the ultraviolet flux of late-type stars
with the crowding of spectral lines and the possible existence of an
"unknown opacity'' (cf., e.g. Gustafsson 1995), as well as the
dependence of the results of the notoriously uncertain collision cross
sections, e.g. for collisions with H atoms (cf. Steenbock & Holweger
1984). Empirically, #M&Mäckle et al. (1975) and
Ruland et al. (1980),
found a tendency for the low-excitation lines (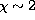 eV) of
FeI and TiI in K giant star spectra to give
systematically lower abundances than the high-excitation lines (
eV) of
FeI and TiI in K giant star spectra to give
systematically lower abundances than the high-excitation lines (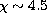 eV). The abundance difference was typically found to be
0.15 dex. Subsequently, Steenbock (1985) succeeded in reproducing
this result with statistical-equilibrium calculations. He found the
effect to mainly reflect an overionization in upper layers (notably
eV). The abundance difference was typically found to be
0.15 dex. Subsequently, Steenbock (1985) succeeded in reproducing
this result with statistical-equilibrium calculations. He found the
effect to mainly reflect an overionization in upper layers (notably
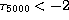 ) of the atmospheres, where the low excitation
lines are formed. The effect is much smaller in the solar spectrum,
leading to systematic errors in a differential analysis where red
giants are compared with the Sun.
) of the atmospheres, where the low excitation
lines are formed. The effect is much smaller in the solar spectrum,
leading to systematic errors in a differential analysis where red
giants are compared with the Sun.
For metal-rich stars, the blocking by the crowd of spectral lines in
the ultraviolet could be expected to - at first sight - strongly
reduce the overionization effect, but this may be compensated for by
a steeper temperature gradient in their atmospheres as a result of
line blanketing effects, as in the case of LiI,
Carlsson et al. (1994), or of CaI, Drake (1991).
The latter study is
particularly instructive for judging the results of the present
investigation. Drake finds that for G and K-type stars the
overionization effects on CaI abundances increase with
decreasing effective temperature, with increasing acceleration of
gravity and with increasing metallicity. At least the last two results
may seem contrary to intuition. They reflect the significance of
HI absorption shortwards of the Balmer discontinuity, which
blocks more of the ionizing UV flux for the giants than for the
dwarfs, and the afore-mentioned effects of metal-line blanketing on
the temperature structure. For the K dwarf stars the effects on CaI abundances may, according to Drake's results, well result in an
underestimate by a factor of two or more if LTE is assumed.
Over-recombination is important for photoionization transitions from
levels close to the continuum (i.e. in the infrared), since for
them the angle-averaged 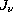 may drop below the local Planck
function deep in the photosphere. This may produce net
recombinations, and overpopulation of the upper levels.
may drop below the local Planck
function deep in the photosphere. This may produce net
recombinations, and overpopulation of the upper levels.
Optical (ultraviolet) pumping occurs in strong lines, e.g. the
resonance lines and is analogous to overionization in that it is
driven by 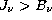 . It is important, not the least when it
occurs in ultraviolet resonance lines and excites the atoms to states
which may be much more easily photoionization due to a much richer
radiation fields available at longer wavelengths, as was early
suggested by Aumann & Woodrow (1975). This is most important for
trace elements, and for metal-poor stars.
. It is important, not the least when it
occurs in ultraviolet resonance lines and excites the atoms to states
which may be much more easily photoionization due to a much richer
radiation fields available at longer wavelengths, as was early
suggested by Aumann & Woodrow (1975). This is most important for
trace elements, and for metal-poor stars.
The complex interplay between these different mechanisms affects most
levels of the atom, at great atmospheric depths, for atoms where the
strong lines get efficiently optically thin in the photosphere,
i.e. for relatively rare elements like the alkalis, while for the
more abundant atoms like Fe and Mg the stronger, e.g. resonance,
transitions are in detailed balance through most of the
photosphere. For these, the relatively simple overionization
phenomenon is probably dominating, except for transitions very close
to the continuum for which e.g. photon suction may be significant.
In a recent study Gratton et al. (in prep.) have used detailed
statistical-equilibrium calculations to explore the departures from
LTE for solar-type dwarfs as well as for red giants of different
metallicities, and their effects on abundance determinations for O,
Na, Mg, and Fe. These authors find relatively small effects for stars
cooler than the Sun for OI - LTE abundances from the IR triplet
lines should be corrected downwards by less than 0.1 dex for stars
with 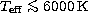 . For NaI the subordinate
lines are weakened by overionization and cascade by about 0.1 dex for
the solar-type dwarfs. The dominating effect for MgI is
overionization, and the non-LTE abundance corrections are thus
generally positive. Typically the corrections are 0.1 dex in the
dwarf stars. For FeI, where again overionization is
dominating the abundance corrections
. For NaI the subordinate
lines are weakened by overionization and cascade by about 0.1 dex for
the solar-type dwarfs. The dominating effect for MgI is
overionization, and the non-LTE abundance corrections are thus
generally positive. Typically the corrections are 0.1 dex in the
dwarf stars. For FeI, where again overionization is
dominating the abundance corrections 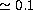 dex. Most of these
effects are found to be greater for
dex. Most of these
effects are found to be greater for 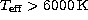 . It should
be noted, however, that models for metal-rich dwarfs with
. It should
be noted, however, that models for metal-rich dwarfs with 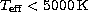 were not included in this study.
were not included in this study.
Summing up the discussion of non-LTE we conclude that the effects on
abundances are expected to be mainly due to overionization for
most of the elements. For the alkali atoms, as well as for the rare
earths, more complex effects may also be significant. Typically, errors
of about 0.1 dex may be expected in the differential results but
the complexity of the interplay between different effects, and in
particular the results obtained by Drake (1991) for CaI, suggest that
greater effects may be present, in particular for the
metal-rich K dwarf stars.
We have shown that errors in fundamental parameters give errors in
mean resulting abundances of less than 0.1 dex. For elemental
abundances derived from several lines this may be the dominating
error, while for abundances derived from one single line errors due to
blends and fitting of continua may be the main contributors to the
overall error. Deviations from LTE in the excitation and
ionization balance may also be of importance, probably more so for
abundances based on few lines, in particular for the K dwarf stars.
We collect our best estimates of errors due to different sources in
Table 5 (click here).
|
Source of error | Error in resulting relative abundance | | | | | | | | |
Measurement of 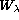 | negligible | | | | | | | | |
|
Continuum fitting | < 0.09 dex, usually 0.05 dex | | | | | | | | |
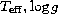 | < 0.1 dex | | | | | | | | |
|
Non-LTE effects | 0.1 - 0.2 dex? | | | | | | | | |
|
Oscillator strengths | <0.1 dex | | | | | | | | |
|
| | | | | | | | | |
Table 5: The effects of error sources explored in this work on
estimates of abundances relative to the Sun
The majority of our stars have not been
studied before through spectroscopic abundance analysis.
Table 6: Comparison of iron abundances between our work and the
abundances quoted in the catalogue by Cayrel de
Strobel et al. (1997). The second column gives our results and the third the
mean, and the spread, of the iron abundances given by Cayrel de
Strobel et al. In the fifth give the number of derivations used. A
straight mean has been taken to represent the mean abundance from the
catalogue
For those of our stars (HD 30562, HD 32147, HD 67228, HD 1319777,
HD 182572, HD 186427) that are in the catalogue by Cayrel de
Strobel et al. (1997) the agreement between iron abundances derived in this study
and those listed in the catalogue is good, cf. Table
6 (click here).
HD 32147 has been given much attention in the discussion of Super
Metal Rich (SMR) stars. SMR stars have been defined as stars with
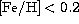 dex (for a discussion and references on SMR stars see
Taylor 1996). Low resolution work and photometric determinations of
[Fe/H] have been carried out for this stars, but this is, to our
knowledge, the first high dispersion analyses of the star. Our [Fe/H]
of 0.28 dex implies that this star is really an SMR star.
dex (for a discussion and references on SMR stars see
Taylor 1996). Low resolution work and photometric determinations of
[Fe/H] have been carried out for this stars, but this is, to our
knowledge, the first high dispersion analyses of the star. Our [Fe/H]
of 0.28 dex implies that this star is really an SMR star.
Our results for HD 182572 are compared with the results of the detailed
analysis by McWilliam (1990) in Table 7 (click here). We note that
considerable discrepancies remain even after correcting for the
difference in effective temperatures.
|
| Mc William | This work | |
|
| | 5739 K | 5380 K | |
|
FeI | 0.31 | 0.42 | 0.24 | |
|
SiI | 0.28 | 0.51 | 0.47 | |
|
CaI | -0.11 | 0.42 | 0.21 | |
|
ScII | 0.14 | 0.36 | 0.36 | |
|
TiI | -0.02 | 0.50 | 0.21 | |
|
VI | -0.02 | 0.44 | 0.12 | |
|
CoI | 0.18 | 0.58 | 0.29 | |
|
NiI | 0.00 | 0.46 | 0.24 | |
|
EuII | 0.18 | 0.13 | 0.13 | |
|
| | | | |
Table 7: Comparison of abundances, [X/H], derived for HD 182572
(HR 7373) in our study and by McWilliam (1990). McWilliam uses
(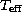 /logg/[Fe/H]/
/logg/[Fe/H]/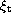 ) = (5380/3.92/0.15/1.9) and
we (5739/3.83/0.42/1.9). The results by McWilliam have been
scaled to the same solar abundances as we use, Table 2 (click here),
(this is most important for iron). In the last column our values are
scaled to the effective temperature used by McWilliam
) = (5380/3.92/0.15/1.9) and
we (5739/3.83/0.42/1.9). The results by McWilliam have been
scaled to the same solar abundances as we use, Table 2 (click here),
(this is most important for iron). In the last column our values are
scaled to the effective temperature used by McWilliam
Table 9: The first column for each star contains the result of this
work, the second the difference between the two studies, Diff = this
work - Edvardsson et al. (1993a). Stellar parameters used by
Edvardsson et al. are for HD 30563 (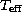 /log
g/[Fe/H])=(5886/3.98/0.17), for HD 67228 (5779/4.20/0.04) and for HD 144585
(5831/4.03/0.23). The values of the parameters used in this study may
be found in Table 1 (click here)
/log
g/[Fe/H])=(5886/3.98/0.17), for HD 67228 (5779/4.20/0.04) and for HD 144585
(5831/4.03/0.23). The values of the parameters used in this study may
be found in Table 1 (click here)
|
| HD 30562 | HD 67228 | | | | | |
|
| | Diff. | | Diff. | | | | | |
|
[OI] | | | 0.21 | 0.01 | | | | | |
|
NaI | 0.21 | -0.02 | 0.23 | +0.03 | | | | | |
|
MgI | 0.33 | 0.12 | 0.23 | 0.09 | | | | | |
|
AlI | 0.25 | -0.01 | 0.22 | 0.03 | | | | | |
|
SiI | 0.21 | -0.04 | 0.27 | 0.12 | | | | | |
|
CaI | 0.17 | -0.06 | 0.15 | 0.08 | | | | | |
|
ScII | 0.31 | 0.06 | 0.33 | 0.16 | | | | | |
|
TiI | 0.13 | -0.12 | 0.09 | -0.02 | | | | | |
|
VII | 0.10 | -0.16 | 0.12 | 0.01 | | | | | |
|
CrI | 0.18 | -0.02 | | | | | | | |
|
CrII | 0.17 | -0.05 | 0.18 | 0.02 | | | | | |
|
FeI | 0.19 | -0.02 | 0.16 | 0.07 | | | | | |
|
FeII | 0.16 | -0.04 | 0.22 | 0.10 | | | | | |
|
NiI | 0.17 | -0.08 | 0.14 | 0.01 | | | | | |
|
YII | 0.09 | -0.12 | 0.12 | 0.06 | | | | | |
|
ZrI | 0.65 | 0.39 | | | | | | | |
|
EuII | 0.14 | -0.17 | | | | | | | |
|
| | | | | | | | | |
Table 10: Comparison between results of our analyses for HD 30592 and HD 67228,
with the results of Tomkin et al. (1997). The second and fourth column
give the results of this work, while the third and fifth give the difference
between this work and that of Tomkin et al. Stellar
fundamental parameters of Tomkin et al.
were (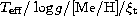 ) =
(5930/4.20/0.21/1.55) and (5835/4.10/0.09/1.75) for HD 30592 and HD 67228,
respectively. Our
parameters are given in Table 1 (click here)
) =
(5930/4.20/0.21/1.55) and (5835/4.10/0.09/1.75) for HD 30592 and HD 67228,
respectively. Our
parameters are given in Table 1 (click here)
We have analysed three stars previously studied by
Edvardsson et al. (1993a). The results are compared in Table 9 (click here). For
HD 30562 and HD 144585 the results agree to within the errors quoted.
The results for HD 67228 show larger discrepancies than the other stars
for magnesium, silicon, calcium and iron. A higher microturbulence
parameter, as used in Edvardsson et al. (1993a), would decrease our
results by 0.01 or 0.02 dex (ionized iron by
0.04 dex).
Edvardsson et al. (1993a) find that a change in 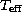 by +100 K gives an
iron abundance 0.06 higher for their stars. Thus, the increase of 52 K
needed to transform the results of Edvardsson et al. (1993a) to our
temperature scale means an increase of their iron abundance by
0.03 dex. Also the silicon and calcium abundances are affected in the same
way as iron while all the other abundances remain as before, within
the errors, in the two studies. The loggf-values agree well (0.06
difference, we have the higher value). The spectrum we have obtained
for this star is of high quality (S/N
by +100 K gives an
iron abundance 0.06 higher for their stars. Thus, the increase of 52 K
needed to transform the results of Edvardsson et al. (1993a) to our
temperature scale means an increase of their iron abundance by
0.03 dex. Also the silicon and calcium abundances are affected in the same
way as iron while all the other abundances remain as before, within
the errors, in the two studies. The loggf-values agree well (0.06
difference, we have the higher value). The spectrum we have obtained
for this star is of high quality (S/N 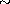 200). We do not find the
discrepancy between the two studies alarming. HD 67228 has also been
studied by Andersen et al. (1984) in a study on lithium isotope ratios
in F and G dwarf stars. They derive an [Fe/H] of 0.05 from spectral
lines using a model with (
200). We do not find the
discrepancy between the two studies alarming. HD 67228 has also been
studied by Andersen et al. (1984) in a study on lithium isotope ratios
in F and G dwarf stars. They derive an [Fe/H] of 0.05 from spectral
lines using a model with (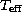 /log
g/[Fe/H])=(5850/4.2/0.05).
/log
g/[Fe/H])=(5850/4.2/0.05).
Two stars from our sample, HD 30562 and HD 67228, were recently
analysed in detail by Tomkin et al. (1997) on the basis of different
spectra; however, obtained with the same instrument and analysed
independently with model atmospheres computed with the same computer
program. The results are compared with those of our analyses in Table
10 (click here). In view of the errors in these analyses we find the
agreement satisfactory.
HD 186427 (16 Cyg B) have been extensively studied, in particular in
connection with searches for solar twins. A recent spectroscopic study
has been performed by Friel et al. (1993). The results are in good
agreement, Table 8 (click here). However, we find lower iron
abundances derived from FeII lines than Friel et al. (1993)
do. This difference is probably mainly due to the different surface
gravities used.
To conclude, we find that, for those few stars in our programme in
common with other studies, abundances are rather well
reproduced. This gives confidence when we now apply
our results to the exploration of
the chemical evolution of the Galaxy.


Up: Abundances in metal-rich
Copyright by the European Southern Observatory (ESO)