4. Model calculations

The model calculations in this study are, as mentioned earlier, inspired by the work of Brandt et al. (1994). The concept is to simulate differential observations of the CMBR with contaminating foreground sources on a single-pixel basis, to add realistic instrument noise and then try to recover the original model parameters by using a non-linear least-squares spectral fitting technique.

By doing so, one should be able to address the very important issue of how well PLANCK and other mission concepts will be able to extract the anisotropies in the CMBR in the presence of hampering foregrounds.

A number of simplifying assumptions are made both with respect to the instrument, the simulated observations and in the actual fitting process. These assumptions, the models and the fitting are described below:

4.1. The instrument

• Frequency bands are assumed to have a zero bandwidth.
• For PLANCK and parts thereof noise (sensitivity) assumes a 2 year mission, an angular resolution of 30' for all bands and only gaussian noise. See Table 1 (click here) for a listing of the assumed noise-levels (or sensitivities) in the frequency bands.
• For MAP noise (sensitivity) assumes a 1 year mission, an angular resolution of 18' for all bands and only gaussian noise. See Table 2 (click here) for a listing of the assumed noise-levels (or sensitivities) in the frequency bands.
• Modelling is done on a single-pixel basis only regarding measurements in one resolution element (pixel) of the size arcmin² for PLANCK and arcmin² for MAP.

The fact that the modelling is done on a single pixel basis implies that any spatial correlation in the CMBR and in the foregrounds is ignored, which will make the modelling a conservative estimate.

4.2. The simulated observations

The following contaminating foregrounds are included in the simulated observations: Synchrotron radiation, free-free emission and galactic dust emission. The total model used to produce the simulated observations is given by:

where

Here , where = 2.728 K and is allowed to vary within K. is given in Table 1 (click here) and 2 as the sensitivity in intensity and G is a gaussian random variable yielding random values with and .

The parameters and parameter ranges for the foregrounds, originally adapted from Fig. 2 (click here) in Bennett et al. (1992), are given below with GHz and all intensities given in units of 10^-20 erg s^-1 cm^-2 Hz^-1 sr^-1.

Synchrotron radiation:

= -0.93

= 0.89 = =

Free-free emission:

= -0.12

= 2.11 = =

Dust emission:

= 3.43

= 3.72 = =

When the two-temperature dust model is used, is given by:

In this model the parameter and range is given with GHz by:

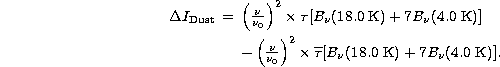
Dust emission:

= 0.3 =

The allowed ranges of foregrounds are sketched in Fig. 1 (click here). These ranges of model parameters yield sky brightness contributions corresponding to situations which can be encountered in most of the sky. The exact fractions are: 99.6% of the entire sky for the synchrotron radiation, 86% of the entire sky for the free-free emission and 100% of the entire sky for the power-law dust. The two-temperature dust parameters cover 100% of the areas at high galactic latitudes, where very cold dust is located according to Reach et al. (1995), corresponding to about 20% of the entire sky.

These estimates of the parameter coverage are made by using various all-sky maps and extrapolating the intensities produced by the parameter ranges given above to these maps thus estimating the sky coverage.

For the synchrotron radiation the Haslam et al. (1982) map was used and for the dust emission the DIRBE 240 m map used. Since no direct map of the galactic free-free emission exists the assessment of the free-free coverage was made using the relation between H and free-free emission discussed by Reynolds (1992) and Bennett et al. (1992).

For each model a set of parameters (, , , , and either and or depending on the dust model) is chosen randomly staying within the limits listed above and sketched in Fig. 1 (click here). Using Eq. (5) the observed differential intensity, , is then calculated for each frequency band.

4.3. The parameter recovery process

The recovery of the model parameters was performed by fitting a function similar to Eq. (5) to the simulated observations. The fitting was performed using the programme ADAPTION (Brosa 1994) for non-linear least squares fitting. This programme uses Gauss' method for least squares fitting as described by e.g. Press et al. (1989) whereas Brandt et al. (1994) use the Levenberg-Marquardt method (also described by Press et al. 1989). As Brandt et al. (1994) we have taken great care to prevent local minima from contaminating our results.

Important assumptions regarding the fitting are made:

• Combined synchrotron radiation and free-free emission are fitted using a single power-law.
• The power-law dust model is fitted with a power-law.
• The two-temperature component dust model is fitted with a two-temperature component model, but with the coldest dust temperature chosen 1 K too high (i.e. 5 K compared to 4 K in the simulated observations). The reason for introducing this temperature difference in the fitting of the cold dust component is to investigate the effect of our limited knowledge of such a component with a temperature close to that of the CMBR black-body.

The function which is fitted to the simulated observations is thus given by:

where

Here = + = 3.00 and = = -0.54.

For the case where the dust is modelled with a two-temperature component model is given by:

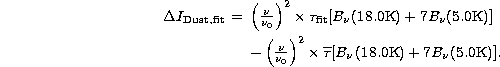
Note the 1 K difference in the coldest dust temperature between the simulated observations and the model fitted to the data.

In order to get a statistical sample 100 different models are calculated and the difference between the input parameters (, ( + ), , and or ) and the fitted parameters (, , and and or ) are registered (e.g. ). From these differences means and standard deviations are calculated.