As mentioned earlier, the development of detector technology is advancing rapidly, producing detectors for CMBR experiments with very low noiselevels as indicated in Tables 1 (click here) and 2 (click here). Thus, the main obstacle for at least space based experiments is the contribution from different galactic and extragalactic foreground sources to the emission in the microwave and FIR sky.
The galactic foregrounds are identified as:
Only Jupiter will enter the field of view resulting in some loss of sky coverage. The planet can and will on the other hand be used for calibration purposes.
The effect of extragalactic sources on the observation of CMBR
anisotropies has been studied extensively by e.g.
Franceschini et al.
(1989).
Their results show, that point source confusion mainly becomes a problem on
the 
level at angular resolutions better than
30' at least for the 50 to 200 GHz range. At higher frequencies
IR point sources become increasingly troublesome.
With regards to the diffuse galactic emission Tegmark & Efstathiou (1996)
find that the fluctuation power spectrum of these foregrounds is roughly
consistent with 
assuming a coherence
scale of 
corresponding to about 
. This implies
that fluctuations in the galactic foregrounds will be of less importance for
higher 
i.e. smaller angular scales.
In the following a discussion of the foregrounds included in the modelling in this work is given. These include only galactic sources since the modelling is done only for a 30' angular resolution for all frequency bands for the PLANCK mission and parts thereof and for an 18' resolution for the MAP mission i.e. at angular scales where fluctuations from extragalactic sources are largely negligible.
The galactic synchrotron radiation is produced by Cosmic Ray (CR) electrons
spiraling in the
magnetic field of the Galaxy. It can be shown, that the emissivity and thus
the intensity of the
synchrotron radiation as a function of frequency follows a power-law if the
energy spectrum for
the CR electrons is assumed also to follow a power-law. The latter has been
empirically established
by means of observations of CR electrons close to Earth (e.g.
Salter &
Brown 1988). The intensity
of the galactic synchrotron radiation can thus be expressed as:
Here 
, where 
is the spectral index for the
CR electron energy spectrum.
Radio surveys made at 408 MHz covering the entire sky with an angular
resolution of 51' (Haslam et al. 1982) and at 1420 MHz
covering the northern hemisphere down to declination 
with a
34' resolution (Reich 1982 and Reich & Reich 1986) show, that
there is a rather significant variation of the spectral index. A variation of
from 1.3 to 0.1 with a mean of
0.7 at declinations spanning from 
to 
was found by
Brandt et al. (1994) by fitting spatially corresponding pixels of the
two surveys and then fitting to a power-law.
But not only does the spectral index vary with position - it also tends to steepen with increasing frequency (Lawson et al. 1987). This steepening is thought to be induced by diffusive shock acceleration of the CR electrons perhaps caused by supernova explosions.
The overall picture is thus very complicated. The radiation depends on several parameters like electron density, electron energy distribution and magnetic field strength, which are not well known or rather not known for every position in the Galaxy. The only way to make significant progress in the attempts to describe the galactic synchrotron radiation is, by making high sensitivity, multifrequency measurements covering the entire sky with constant, high angular resolution and beam pattern. Such work by others is in progress (Danese et al. 1996) and should soon yield results.
The PLANCK mission will however produce high quality maps of the entire sky at frequencies where synchrotron radiation dominates. Such maps will be of great importance for constraining models for this radiation source. It will also make PLANCK more independent of ground-based observations and will thus play a significant role in the actual data processing.
In the present study, the synchrotron radiation is modelled as a perfect power-law, where both the spectral index and the baselevel are allowed to vary independently within limits, which should be sufficient to model any local variation. The spectral indices used in the models are thus not assumed to be frequency dependent.
The galactic free-free emission originates from free electrons in the approximately 105 K hot ionized interstellar medium (ISM), which are deflected and thus slowed down by ionized atoms, mostly protons. The difference in kinetic energy of the electron before and after the deflection is the amount of energy radiated as free-free emission or "bremsstrahlung''.
Bennett et al. (1992) derive an expression giving the antenna or
Rayleigh-Jeans temperature
induced by the free-free emission as a function of frequency and find that the frequency dependence of the antenna temperature
follows a power-law, 
. The spectral index
is a weak function of
frequency and the kinetic electron temperature. In terms of intensity the
frequency dependence of the free-free emission also takes the shape of a
power-law with a spectral index of 
.
The free-free emission component of our Galaxy is still rather poorly understood in the sense, that no usable all-sky maps exist. Bennett et al. (1992) produced all-sky maps from the COBE DMR data using both a subtraction and a fitting technique. Both maps are noise dominated - especially on small scales - and model dependent, since the modelling of the synchrotron radiation is uncertain (Brandt et al. 1994). Some conclusions can nevertheless be drawn from these maps, namely that the galactic free-free emission almost follows a cosecant-law when going to higher galactic latitudes (Bennett et al. 1992). The maps also show that the bulk of galactic free-free emission is confined in the plane of the Galaxy. This should come as no surprise since the hot, massive stars, which produce the environment suitable for making free-free emission are all located in the galactic plane (Partridge 1995).
Besides this work by
Bennett et al. (1992) there is another approach
based on a relation between
the intensity of H and free-free emission as discussed by
Reynolds
(1992). Unfortunately no
full sky survey of the interstellar H background exists yet so this
method can only be used as an
further estimate of the distribution of the free-free emission. Such
estimates confirm the
cosecant-law found by Bennett et al. (1992).
Kogut et al. (1995) have reported a spatial correlation between
free-free emission and galactic
dust emission (see below) on angular scales larger than the 
COBE
DMR beam. They conclude that if this correlation holds to smaller angular
scales, free-free emission should be a less
significant contaminant for anisotropy measurements on degree scales at
frequencies above 20 GHz.
This is confirmed by recent work by Simonetti et al. (1996), which
indicates that free-free emission contribution to
fluctuations at 27.5 GHz are negligible to CMBR anisotropies on
degree-scales. These results were
obtained by making sensitive H images and comparing these with recent
data from the Saskatoon CMBR experiment.
Even though the lack of surveys of the galactic free-free emission leaves many open questions, the situation is a bit more relaxed than with respect to the synchrotron radiation since the possible range of parameters, like spectral index, are more constrained, as the physical processes causing the free-free emission are less sensitive to local changes in the environment (e.g. kinetic electron temperature).
In this work the free-free emission is modelled as a perfect power-law, as is the synchrotron radiation, where both parameters are allowed to vary within reasonable limits, in order to cover the resulting emission range produced by local variations.
The galactic dust consists of conglomerates of molecules in a range of sizes
from 
Å to 
m, of which most are formed in the "cool"
atmospheres of red giant stars and from there ejected into the ISM.
Here the dust grains can be heated by the photon flux from stars and will
then seek thermodynamic equilibrium by emitting radiation in the
IR or the FIR part of the spectrum
(see e.g.
Alexander & Ferguson 1994; Sedlmayr 1994; Knapp 1991).
Dust will radiate as a grey-body, meaning that the
emission spectrum for the dust will be a black-body corresponding to the
equilibrium temperature, T, of the dust modified with a frequency
dependent emissivity conventionally given as 
(Banday & Wolfendale 1991).
The intensity of dust emission from a population of dust grains heated to
the temperature, T, would then be:
where 
is the black-body radiation
corresponding to the temperature, T.
The spectral index,
, depends on the atomic and geometric structure and composition of
the dust grains (Banday & Wolfendale 1991). Detailed calculations and
laboratory experiments have demonstrated that
for larger grains, whilst smaller grains tend to index
values lower than 2.
Due to the contaminating effect of the Earth atmosphere, most information about the galactic dust emission is supplied by observations made by satellites i.e. IRAS and COBE.
Especially the COBE FIRAS and DIRBE instruments have provided vast
amounts of information about the galactic dust at IR and FIR wavelength.
Wright et al. (1991) reported preliminary spectral observations of
the Galaxy by FIRAS, stating that there are two major components in the
spectrum of the Galaxy, namely a continuous component due to heated dust
and strong line emission from the 158 
m line of singly ionized carbon.
With respect to the continuum, Wright et al. (1991) split the dust
emission into two functions - one of position
(i.e. galactic longitude and latitude) and one describing the spectral
behaviour (
). In order to determine the spectral behaviour
Wright et al. (1991) tried out different forms of analytic fits with
functions of the form given by Eq. (2).
They found that the best fit was obtained with the expression:
where the term 
represents the galactic synchrotron radiation
component. They obtained an even better fit, when introducing a cold dust
component with a temperature of 4.77 K:
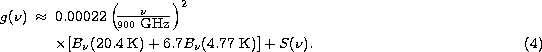
The better fit by the two-temperature dust model is due to the
fact, that the FIRAS data exhibit an excess of emission at long wavelength.
The 4.77 K black-body emission supplies the excess needed to fit the data.
Similar spectral fitting, also based on the FIRAS data, has been performed
by Reach et al. (1995). They also find evidence for a widespread, very
cold (4-7 K) dust component, which has an optical depth that is
spatially correlated with the "warm'' (
K) dust.
They argue that the cold component could either be a result of enhanced
emissivity of the warm dust at submilimeter wavelength or be caused
by a so far unknown population of dust grains.
The subject is nevertheless controversial since Boulanger et al. (1996) find, that the emission excess which Wright et al. (1991) and Reach et al. (1995) interpret as a cold component is not correlated with the 21 cm emission which traces the neutral hydrogen. Boulanger et al. (1996) conclude that the excess is either due to an unknown extragalactic source or caused by the FIRAS instrument. The work of Kogut et al. (1995), which indicates a correlation between the galactic free-free and dust emission does not exclude the possibility of a cold dust component but does not support it either.
Results from the COBE DIRBE instrument are not able to settle this
dispute since the longest wavelength utilized by DIRBE is 240 m.
Any dust component radiating at 5-10 K would not contribute significantly
to the intensity at 240 m implying that such a component would
remain largely undetected by DIRBE (Sodroski et al. 1994).
In this discussion one could find arguments to support the modelling of
the galactic dust emission both as a two-temperature and a
single-temperature dust. There is however a less complicated approach,
which can be used. No matter whether the dust consists of one or more
components, the Rayleigh-Jeans part of the dust spectrum can be approximated
as a perfect power-law. Since the baseline frequency coverage of the
PLANCK mission only just stretches further than the Rayleigh-Jeans part
of the black-body for a 20 K dust component, the galactic dust emission
is in this work modelled both as a two-temperature dust with a very cold
component and as a perfect power-law with simultanious varying baselevel and
spectral index covering all possible dust emission intensities demonstrated
by the DIRBE 240 m map extrapolated to the wavelength range of PLANCK.