Preliminary results obtained with the technique in its standard version were already presented elsewhere (Carbillet et al. 1996b). We give here a more accurate application of the technique in its two versions to three binary stars for which the observing conditions are reported in Table2. All the data reduced in this section consist of high-light level speckle frames of

pixels. We give in what follows a detailed description of the analysis for each object.

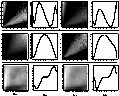
Figure 6: Top: linear gray-level representation of

a) and

c), together with plots of the corresponding radial integrations-- b) and d) --for the binary

Del. Middle: Q a) and

c), and the corresponding radial integrations-- b) and d) --for the binary Moaï 1. Bottom: the same as in Top for the binary

Per

**Table 2:** Observation table of the three sets of data processed in Sect. 6. The right ascension, the declination and the combined magnitude in the red ( m_R ) are given, together with the telescope used (WHT = WilliamHershellTelescope, LaPalma, Spain-- BLT = BernardLyotTelescope, PicduMidideBigorre, France), the observing wavelength /bandwidth in Å, the approximate average value of the Fried's parameter r₀ , the exposure time and the date of observation
star name	r.a. _2000.0	dec. _2000.0	m_R	Telescope		<r₀>		Date
Del			3.2	2m BLT	6580/425	cm	20 ms	11/09/94
Moaï 1			6	2m BLT	6500/700	cm	20 ms	12/12/95
Per			2.3	4.2m WHT	6580/425	cm	25 ms	19/01/95

6.1.

Del

The subgiant

Del is a close binary of 26.6 years of period given as a standard star for binary-star interferometry by McAlister & Hartkopf (1983). The latest orbit is computed by Hartkopf et al. (1989). The reference star observed was

Del from which we used 410 frames, and 324 for the binary.

The separation angle d and the PA from which we derived an estimation of

were computed from the classical calculation of the visibility function, founding:

and

Figure 6 (click here), first row, shows both the quantities

and

, with their radial integrations

and

, derived from the twofold PDFs of the binary and of the reference star computed for the space-lag vector

, and from the twofold PDF of the binary computed for

. From these quantities, we could deduce the value of

for which they are extrema by the procedure described in Sect. 5 (click here). So we have:

using the standard version; or:

using the reference-less version. The exact value of the intensity ratio, giving then both the orientation and a relative photometry of the binary system, is found to be

(or

), that corresponds to a magnitude difference

(or

). This is in agreement with the value given by Couteau (1962)-- i.e. 0.9 --if one considers that

is roughly similar to

for this object. Moreover, since we found an intensity ratio smaller than 1, we can assume, given the orientation of the frames and

, that PA is 288

and not 108

. This is anyway what was expected from the orbit cited before.

It is interesting to note that the two versions of the method give, for these data, an equivalent result, even if the relevant ridge seems to be better defined using the reference star data.

6.2. Moaï 1

The close double star Moaï 1 (SAO12917) was discovered during the observation from which the data used in this section are extracted. The approximate period evaluated by Carbillet et al. (1996c) is

years. The separation vector

was deduced from this last paper using the cross-correlation technique (Aristidi et al. 1996). This corresponds to:

and

. The reference star observed was SAO12929 from which we used 2617 frames, and 2619 for the binary.

Figure 6 (click here), second row, shows both the quantities Q and

, with their radial integrations I_Q and

. The value of

derived from these quantities is:

-- or

. The deduced value of

is then:

(or

), that corresponds to a magnitude difference:

(or

). This is in agreement with the value computed in the paper cited before and using both the cross-correlation technique and the fork algorithm (Bagnuolo 1988)--

and

. The position angle is then confirmed to be:

and the magnitude difference between the companion and the primary star in the red:

We can say that, here again, the method seems to take advantage of its use with the data of the reference star, the reference-less method giving anyway an acceptable value of the intensity ratio.