We assumed in writing the equations in the previous sections that 
, i.e. the separation between the components d is large with respect to the speckle size s . In practice, the interesting point for observations is when 
, since the aim of every speckle imaging technique is to reach as close as possible the diffraction-limited resolution of the telescope. Then, in order to complete the theoretical study and test the validity and limits of it for practical speckle observations, we chose to make several numerical simulations with different values of d and 
. We decided not to report all these simulations in this paper but just the most interesting ones, i.e. for a separation 
, and for three different relevant values of .
The functions Q and 
are respectively obtained by dividing the twofold PDF of the binary star computed for 
by that of a point-source, and by that of the binary computed for 
. In order to avoid zero divisions during this operation, we made use of an iterating
algorithm based on Van Cittert (1931) and already applied to speckle data by
Cruzalèbes et al. (1996). The output estimate of this algorithm perfectly converges to the solution of the normal division after an infinite number of iterations. Let be 
. If 
the calculation of A may rapidly diverge. One estimate of A can then be:
Because 
, it is easy to demonstrate that 
. In the case where the denominator C becomes smaller than the limit for which the machine cannot see the difference between 1 and 1+C , we found that it is typically sufficient to perform about ten iterations to estimate the ratio. In the other case, we simply calculated the ratio by normal division.
We also computed the quantity Q-QT to enhance the relevant ridge, where QT is the transpose quantity of Q .
The radial integration of this quantity 
is related to IQ by:
So its ideal expression (i.e. when 
) follows:
In the present case 
is obviously finite and the general behavior of 
is to have a maximum for the right value of , like 
, but a minimum too for 
. For such a quantity the extrema are better defined. A second interest is that it could stand out better between a value of close to but greater than 1 and a value of close to but smaller than 1.
In practice, to estimate 
, we did not directly make use of Q . We computed
in order to have two different estimates (as PS(2) is determined experimentally) of the intensity ratio when analyzing the quantity 
: one corresponding to the maximum of the radial integration, and one to the minimum. The output values of 
are then averaged from these two estimates, together with the corresponding errors.
In addition, and in order to get rid of the effect of statistical fluctuations and to keep only the most significant features, we also smoothed the Q , , and 
estimates by convolving them by a 
unit valued filter.
We consider only the part of the computed quantities Q , , and where the signal-to-noise ratio is the best, i.e. where there is a significant number of events in the twofold PDFs of the reference and the binary star. This typically corresponds, in our present case, to an extraction of 
pixels near the origin for PDFs computed with a sample of the intensity of 256 levels.
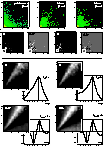
Figure 4: Top, first row: logarithmic gray-level representation of
the twofold PDFs computed for the simulation made for 
and (dx,dy)=(+3,+4) . Top, second row: linear gray-level representation
of the corresponding Q , ,
and functions. The white squares show the
extraction zone used for the computation of the radial
integrations. Bottom: extraction of Q , ,
and , together with their respective radial
integrations. Its extrema are outlined by dashed lines
The simulation work presented in this subsection made use of two data sets (one for the binary star and one for the point-source), each made of 100 speckle frames of 
pixels, simulated with the following parameters:
Å,
pixels 
pixels,
.
In Fig. 4 (click here) we represent the PDFs obtained for the point-source for , and for the binary for and for . The functions Q and are deduced from this, and represented together with their radial integrations. The functions and are represented as well with their radial integrations.
Figure 5: Left: linear gray-level representation of and
for 
, together with the plots
of and 
.
Right: linear gray-level representation of and
for 
, together with the plots
of , , 
and
|
input | input | Q | | | |
| 1.5 | 56.31 |  |  |  |  |
| 10 | 84.29 |  |  | |  |
| 1.01 | 45.28 |  | >45 |  | >45 |
The procedure to quantitatively find the extrema of these radial integrations and to estimate the respective errors makes use of a polynomial fit of these quantities around the extrema. We chose for this purpose to fit the
region surrounding the extrema by a polynomial of the second degree, since close to its maximum a convex function is supposed to have a quadratic-like behavior.
The values of 
found from the four quantities , , and are reported in the first row of Table1. The values found for Q and are rather less than the input value of . This means that there is a systematic error in detecting the right value of from the maximum of IQ and 
. However this systematic error is not present, or at least in a very small way, in the case, not presented in this paper, where the separation d is actually large with respect to s . Nevertheless, this systematic error is avoided by considering the values of found for and . So while Q or gives us a first (but biased) estimate of , the computation of or then gives us a good value of it. The general procedure will be to consider directly or to estimate the intensity ratio of a binary star. Finally, this method gives equivalent results by using it in its reference-less version or in its standard version.
We made several numerical simulations in order to test the validity and limits of the method. This showed us that two kind of limiting cases exist depending on .
In order to better test the limiting cases of the method, we chose to make the simulation with a larger number of frames per set: 1000. The first limiting case is when is large (or small) with respect to 1. This corresponds to a large magnitude difference between the components of the binary star. This is already a well-known limit of speckle observations but in our present case, this corresponds to a ridge of the Q function close to the axis 
(or 
), implying then a difficult determination of the right value of . We found, with the typical parameters taken here, that the useful limit of the method is for 
(and for 
), i.e. for a magnitude difference of 
. As shown in Table1, second row, the computations Q and could only give an idea of , and we deduce from IQ and that is greater than or of the order of 
. The estimate of is still available from and 
but gives a slight under-estimate.
The second limiting case is when is close to 1. This problem occurs when the two components of a binary system are of close magnitudes, implying then an ambiguity in the determination of the PA. In that case, the quantities and become very small but still contain the information about the orientation of the binary, even if the precise determination of is no longer possible. Nevertheless, Q and can in this case give a good estimate of it, as shown in Table1, third row, where we report the result of a simulation made for (i.e. for a magnitude difference of 
0.01).
Figure 5 (click here) illustrates the procedure used to analyze these two limiting cases. In the first case ( ), is directly determined from the extrema of or . In the second ( ), is determined from IQ and and the orientation is checked from or . An interesting case is presented by the reference-less version of the method. In fact, while shows a maximum for slightly smaller than 45
(but with an error large enough to include the value 45), the shape of clearly denotes a value of greater than 45. In conclusion, a good estimate of can be found by using our method if the following procedure is performed:
.
is not close to 1: estimate it with or .
is close to 1: estimate it with IQ or and check the orientation (i.e. check if is greater or not than 
) by using or .
An application of this procedure to real data of close visual binary stars is performed in the next section, together with a comparison with the results found elsewhere.
) found for the numerical simulations