In practice, this integral must be transformed into the summation
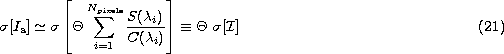
where
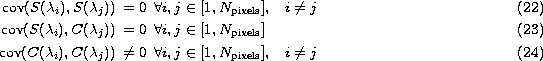
since
After some manipulation the covariance terms are
where we have defined the following four parameters

Since Sb y Sr are not correlated, we obtain
and finally
where
We have derived a more accurate set of
analytical formulae to compute errors in line-strength indices.
The expected random error
in the measurement of an atomic index is given by
![]()
In practice, this integral must be transformed into the summation
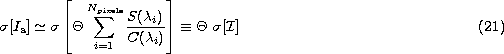
where ![]() is the dispersion (in Å/pixel), assuming a linear
wavelength scale, and
is the dispersion (in Å/pixel), assuming a linear
wavelength scale, and ![]() the number of
pixels covering the central bandpass (note that, in general, fractions of
pixels must be considered in the borders of the bandpasses).
the number of
pixels covering the central bandpass (note that, in general, fractions of
pixels must be considered in the borders of the bandpasses). ![]() is a
function of
is a
function of ![]() variables
variables
![]() which verify
which verify
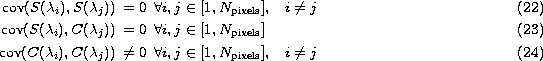
since ![]() is computed from Eq. (5 (click here)). Taking this
result into account:
is computed from Eq. (5 (click here)). Taking this
result into account:
![]()
![]()
![]()
![]()
![]()
After some manipulation the covariance terms are
![]()
![]()
![]()
where we have defined the following four parameters

Since Sb y Sr are not correlated, we obtain
![]()
and finally
![]()
![]()
where
![]()
![]()
![]()
Errors in the molecular indices are calculated through
![]()
which is identical to Eq. (12 (click here)).
Using the new formulae, the computed index errors for the samples presented in Figs. 2 (click here) and 3 (click here) completely agree with the results from numerical simulations (see Fig. 4 (click here)).
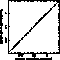
Figure 5: Comparison of the Mg2 relative errors employing the new
formulae and numerical simulations for the samples shown in
Fig. 3 (click here). The agreement between both methods is
complete
The errors in the
4000 Å break, defined in Eq. (8 (click here)),
can be computed as
![]()
where
![]()
![]()
(the subscript p refers indistinctly to b or r).
Note that in this case ![]() and
and ![]() are not correlated.
D4000 errors computed in this way show a perfect agreement with
numerical simulations.
are not correlated.
D4000 errors computed in this way show a perfect agreement with
numerical simulations.