In the present section we apply the three methods to two real
one-dimensional astronomical data samples: 301 measured redshifts for
the cluster of galaxies Abell 3526 (Dickens et al. 1986) and a
redshift sample of 82 galaxies in the region of Corona Borealis
(Röder 1990).
The Abell 3526 cluster was already considered by
Pisani (1993) in order to study the performance of the adaptive kernel
method. Abell 3526 is a bimodal cluster in the redshift space (see
e.g. Lucey et al. 1986) and it provides us with an example of
moderate complexity, intermediate between examples B and D. Fig. 7 (click here)
shows the kernel and wavelet estimates, as well as the MPL estimate
together with the UCV function allowing one to obtain the optimal
penalization parameter. The bars at the base of the plots stand for
the observed redshifts. The second sample is studied in order to make
a comparison with the results of
Pinheiro & Vidakovic (1995) who
developed another wavelet density estimator based on a data
compression approach. Our estimates with the kernel, wavelet, and MPL
methods are shown in Fig. E8, as well as while the UCV function for
the MPL estimator.
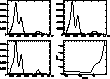
Figure 7: Analysis of the redshift distribution of the A3526 galaxy
cluster. At top are displayed the kernel (left) and wavelet (right)
estimates. At bottom is given the MPL solution with the UCV function
of the estimator. At the base of each estimate, the bars stand for the
observational data. The unit of the x-axis is km s-1
Figure 8: Analysis of the redshift distribution of the Corona
Borealis sample. Definitions are the same as in Fig. 7
Figure 9: The cubic B spline scaling function (left) and the related
mother wavelet (right)
As expected from the numerical simulations, the three methods give
consistent results in both cases. The differences are similar to those
exhibited in the studies described in § 3.4. In fact, the use
of the wavelet estimator results in sharper and more compact
structures when compared to kernel estimates, and it may allow one to
detect small features otherwise missed (e.g. the peak located at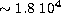 
km/s in Fig. E9). But, as usually, discontinuities at
zero-crossing locations occur in these wavelet-based estimates. The
MPL and kernel solutions are defined as positive, but only MPL
estimates can exhibit regions of null density for local voids in the
data. Hence, the MPL estimates differ from the kernel solutions by
yielding structures with a somewhat smaller support and regions of low
density, similar to those restored in the wavelet-based approach, but
without discontinuity problems (cf. Fig. 1 (click here)).
When dealing with the A3526 data, three structures are detected, in agreement with previous studies. The bimodality of the cluster is confirmed, as well as the existence of a background group 4 000 km/s away from the main structures. The three methods we have used succeed very well in separating the two peaks defining the body of the cluster. The significance of both results is at least at the 3.5 sigma level (cf. the threshold applied to the wavelet coefficients with respect to their statistical significance).
As for the Corona Borealis sample, our results indicate that the distribution of redshifts is composed of a foreground group, a complex central structure and a background population without any clear sign of clustering. The central structure is mainly bimodal, but the overlap between the two peaks with different heights is greater than in the A3526 case. Thus, no firm conclusion about the shape of their profiles can be reached until alternate restorations have been performed (see § 3.5). A small bump before the body of the distribution denotes the presence of an isolated pair of galaxies. With respect to the estimate of Pinheiro & Vidakovic (1995), our solutions are smoother but look similar, except for the smaller background peak of the central structure. According to the previous density estimation, this secondary component is itself bimodal and much more clearly separated from the main peak. This difference comes from the underlying strategies. We are looking for a description in terms of significant structures, whereas an efficient data compression is sought for in the other algorithm. So it appears that Pinheiro & Vidakovic's estimate follows the data more closely than ours, which is not the optimal solution from the density estimation point of view.