3. Numerical simulations

Every density estimator has two conflicting aims: to maximize the fidelity to the data and to avoid roughness or rapid variations in the estimated curve. The smoothing parameter , the penalty parameter and the threshold parameter k control these two aspects of the estimation in kernel, MPL and wavelet estimators, respectively. The choice of these parameters has to be made in an objective way, i.e. without using a priori knowledge about the distribution considered. This is possible by using data-based algorithms, e.g. the unbiased cross validation for the kernel and MPL estimators or the clipping for the wavelet coefficients. These three estimators favor Gaussian or quasi-Gaussian estimates because of the use of a quasi-Gaussian kernel, of the adopted form of the penalty functional, and of the shape of the chosen scaling function.

As for the practical development of the codes, we have chosen for the kernel estimator an Epanechnikov kernel function (see Eq. 5 (click here)), which offers computational advantages because of its compact support.

In the case of the wavelet estimator, we have treated the borders of the interval with a mirror of the data and we have chosen an initial grid of 1024 points in order to recover the finest details of the examples considered. Thus, our results are not hampered by any artificial smoothing related to information lacking at small scales. We have also decided to threshold the wavelet coefficients by using a level of significance of 3.5 standard deviations (i.e., the probability of getting a wavelet coefficient W greater than the observed value is less than 10^-4).

In the case of the MPL, the solution greatly depends on the algorithm of minimization used. We have obtained good results with the routine NAG E04JAF (see also Merritt & Tremblay 1994). Obviously, the computational time increases with the number of points of the curve which are considered, i.e. with the number of parameters of the function to be minimized. A good compromise between resulting resolution and required computational time is to use 50 to 100 points. Though the MPL method is very attractive from a philosophical point of view, its practical usage is penalized by these difficulties in minimization. In fact, an extension of the method to a two-dimensional case would become a very hard computational task on account of the high number of parameters involved.

3.1. Description of the samples

We decided to test the previously described density estimators by performing some numerical simulations on several density functions. We considered five examples, covering a large range of astrophysical problems:
A. - a Gaussian distribution: N(0,1);
B. - two similar Gaussians: ();
C. - a Gaussian with a small Gaussian in the tail: ();
D. - a Gaussian with a narrow Gaussian near its mean: ();
E. - a uniform distribution featuring a Gaussian hole: .
The notation stands for a normal random deviate with a mean of and a standard deviation of . One can find these distributions by analyzing the velocity distributions of galaxies in galaxy clusters or of stars in globular clusters. In particular, two similar Gaussians may represent a merging between two clusters, while a Gaussian with another small one may be found in subclustering cases. Finally, the hole may correspond to a local void in a galaxy distribution.

The estimators have to restore a smooth density function from limited sets of data points, so that the estimate suffers from noise depending on the size of the sample. Moreover, the simulations are generated by the usual random routines, which may sometimes lead to experimental data sets in strong disagreement with the theoretical distribution. Therefore, the quality of the restored function must be checked against the number of data points involved (accuracy) and the fidelity of the sample (robustness). One way to get a perfect sample for a number N of events is to consider the canonical transform X=F(x) where F(x) stands for the repartition function. The [0,1] interval is divided into N+1 equal intervals, which yields a set of N nodes x_n by using the inverse transform. At these nodes, the Kolmogorov-Smirnov test is satisfied: by construction, the distance between the repartition function and the cumulative function is equal to zero. Hereafter such samples are called "noiseless'' samples. In order to take into account the noise coming from the finite size of the samples, we considered three data sets with an increasing number of points. In the pure Gaussian example we chose a minimum number of 30 points, below which we decided that the restoration of the parent distribution is too difficult, and two more complete sets with 100 and 200 points, respectively. We considered 50, 100, and 200 points in the second and third examples, whilst in the fourth example we consider 100, 200, and 400 points in order to get a high enough signal for detecting the small feature. Finally, in the case of the hole, we considered a uniform distribution and discarded the 50, 100, and 200 points which fell in the region of the Gaussian hole. Hence, the number of points is on average 430, 860, and 1715 in the three cases. The width of the interval was doubled in order to avoid having edge effects in the central part coming from discontinuities at the limits of the uniform distribution.

3.2. Noiseless samples

First we considered the "noiseless'' samples, which are generated by transforming a regularly sampled uniform distribution into the distributions of the examples described above. The absence of noise allows us to highlight the performance of the methods. In Fig. 1 (click here) we show the estimations by means of the kernel and wavelet estimators. In Fig. E2 (Fig. 2 in the electronic version of the paper) we report the MPL density estimates, while the corresponding UCV curves are displayed in Fig. E3.

  
Figure 1: Kernel and wavelet estimates on "noiseless'' samples. The solid line is the theoretical distribution, the dashed line stands for the kernel estimate and the dotted line corresponds to the wavelet solution. Examples A to E (see the text) are displayed from top to bottom. The number of data points increases from left to right

 
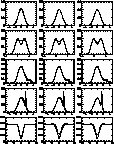
Figure 2: MPL estimates on "noiseless'' samples. The dotted line corresponds to the MPL estimate. The graphs are sorted in the same way as in Figure 1

 
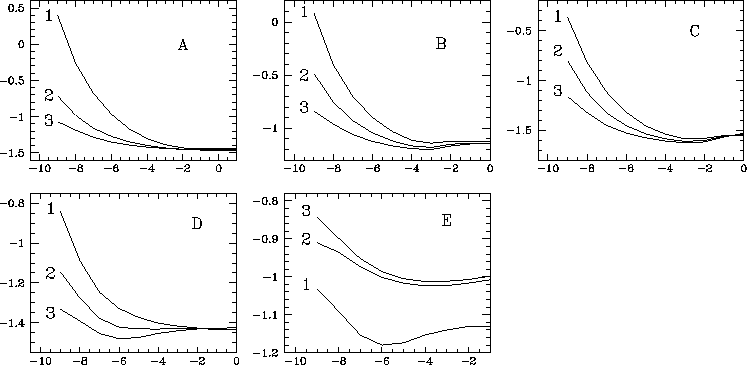
Figure 3: The UCV functions related to the MPL estimator for the "noiseless'' samples. Each graph is labeled according to the corresponding example. The curve labels indicate the increasing sample sizes

The comparison of the whole set of results shows that the three methods detect and retrieve most of the features in more or less the same way, especially in the case of a great number of data. The kernel method yields quite accurate restored density functions in most cases, with the noticeable exception of example C, where the small superimposed Gaussian is never really detected. The same difficulty arises for the MPL estimates. On the contrary, small features are better detected by the wavelet method than by the others. For instance, only the wavelet method is able to detect the small feature of example C and the secondary peak of example D when 100 data points are involved. The results of the MPL method are similar to those of the kernel method. Nevertheless, it appears that the restoration coming from the MPL method is more accurate for the Gaussian tails of the distributions, whereas it fails to detect the secondary peak of example D when the sample size is lower than 400.
As for the MPL estimates, it becomes clear by looking at Fig. E3 that there are some cases where it is not possible to find a minimum of the UCV; in fact, only monotonic decreasing curves are sometimes obtained. This means that a large value of the penalization parameter give a good fit, i.e. the MPL estimate becomes a Gaussian fit of the data (see § 2.3). Moreover, as discussed in the previous section. the MPL method suffers from its dependency on the efficiency of the algorithm of minimization as well as from a computational time which is much higher than for the other two methods. These disadvantages prevent efficient use of the method, especially when high resolution is required. Since the overall performances of the MPL method appear to be very similar to the other methods, we decided to investigate further only the behaviors of the kernel and wavelet approaches. The MPL will be referred to again only when analyzing some real data sets.

Let us now take a close look at the general behavior of both methods by means of numerical simulations. The trends and subtle differences between the kernel and wavelet results will be explained by reference to their underlying mathematical definitions.

3.3. Statistics

We performed 1 000 simulations for each case in order to estimate the variance of the estimated density functions, which is linked to the intrinsic variations in the experimental data set.

In order to compare the two density estimations, we chose to evaluate the results on a grid of 50 points. The theoretical functions (solid line), the median curves of the estimates (dashed line) with their 10 and 90 percentiles (hatched band), which represent a measure of the variance of the estimate, are displayed for each case in Figs. 4 (click here) and 5 (click here) for the kernel and wavelet estimators, respectively.

  
Figure 4: Kernel results from numerical simulations. The graphs are sorted in the same way as in Fig. 1 (click here). Solid lines represent the theoretical distributions; the hatched area is limited by the 10 and 90 percentiles of the results while the dashed line stands for the median solution

  
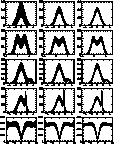
Figure 5: Wavelet results from numerical simulations. Definitions are the same as in Fig. 4 (click here)

 
Figure 6: ISE distributions for the kernel and wavelet estimates corresponding to the samples considered. The graphs are sorted as explained in Figure 1 (click here). The dotted histogram corresponds to ISE values for the kernel solutions, while the solid one displays the distribution of ISE values for the wavelet estimates

These curves show local agreement between the estimates and the true distributions. We decided to get quantitative information about the global quality of the solutions by evaluating the integrated square error for the estimate of each simulation according to the formula:

The distributions of this quantity for the two estimators are displayed in Fig. E6. We report the ISE values for the "noiseless'' estimate in Table 1 (click here).

One of the aims of density estimations from discrete data is structure characterization. Information, viewed in terms of basic structure parameters with respect to the true values, is provided in Table 2 (click here). It gives positions and amplitudes for the peaks which are present in the median estimates. The errors relate to the grid step for the positions and to the 10- and 90-percentile values for the amplitude.

   

Ex. N Kernel Wavelet

A 30 100 200

B 50 100 200

C 50 100 200

D 100 200 400

E -50 -100 -200

Table 1: ISE values for kernel and wavelet estimates on the "noiseless'' samples

 

 

Ex. N Location Amplitude

True Kernel Wavelet True Kernel Wavelet

A 30 0.00 0.40 0.36^+0.11_-0.08 0.39^+0.18_-0.17

100 0.00 0.40 0.38^+0.06_-0.05 0.39^+0.08_-0.06

200 0.00 0.40 0.39^+0.05_-0.04 0.39^+0.06_-0.04

B 50 0.00 0.20 0.17^+0.05_-0.03 0.19^+0.06_-0.05

3.00 0.20 0.17^+0.05_-0.03 0.19^+0.06_-0.05

100 0.00 0.20 0.19^+0.04_-0.03 0.19^+0.03_-0.03

3.00 0.20 0.19^+0.04_-0.04 0.19^+0.04_-0.03

200 0.00 0.20 0.19^+0.03_-0.03 0.18^+0.05_-0.02

3.00 0.20 0.19^+0.03_-0.03 0.18^+0.05_-0.02

C 50 0.00 0.36 0.32^+0.08_-0.07 0.35^+0.08_-0.08

3.00 0.08 0.08^+0.03_-0.03

100 0.00 0.36 0.34^+0.06_-0.05 0.35^+0.07_-0.05

3.00 0.08 0.07^+0.02_-0.02

200 0.00 0.36 0.35^+0.04_-0.04 0.35^+0.06_-0.03

3.00 0.08 0.07^+0.02_-0.01

D 100 0.00 0.36 0.34^+0.09_-0.06 0.35^+0.08_-0.06

1.50 0.52 0.26^+0.10_-0.06

200 0.00 0.36 0.35^+0.08_-0.07 0.35^+0.06_-0.03

1.50 0.52 0.33^+0.14_-0.15 0.37^+0.20_-0.14

400 0.00 0.36 0.36^+0.06_-0.07 0.36^+0.04_-0.04

1.50 0.52 0.39^+0.09_-0.09 0.45^+0.09_-0.10

Table 2: Structure parameters

3.4. Comments

First of all, our study shows that both kernel- and wavelet-based density estimators recover different parent distributions quite well, though some differences in efficiency can be noticed; moreover, in most cases the accuracy of the kernel and wavelet estimations increases with the number of points, while the variance decreases. Let us examine in detail the different examples in order to describe the fine behavior of these estimators, which require approximately the same computational resources.

Example A

When dealing with the experimental set involving a low number of points, we first notice that the variance is larger for the wavelet estimate than for the kernel estimate. In fact, the wavelet transform is as sensitive to voids as to clustering in the data distribution. In the case of few data, significant voids generated by random fluctuations in the numerical set are frequently detected. Therefore, the analysis often ends up with several small clumps instead of a single large cluster with a Gaussian distribution. This increases the final variance of the result. However, the median curve and the "noiseless'' estimate agree fairly well with the parent distribution, except for the tails. In fact, we decided to consider wavelet coefficients computed with fewer than three points as meaningless for statistical reasons. Since there is a low probability of having experimental data points in the tails, this explains why these features are missing both in the median and in the "noiseless'' estimates. Cutting the tails is a general behavior of our wavelet-based density estimates.

On the contrary, the kernel solution presents wider tails than the parent distribution. Wide kernel functions are in fact associated with every point in low density regions (see Eq. A1 (click here)). Thus, as a consequence of normalization, the kernel estimate departs from the true function in the central region in the case of restricted sets of data points. These trends are verified for every example in our study. Further information is provided by Fig. E6 which shows that the global agreement with the theoretical function is better for the kernel than for the wavelet estimate when noisy data are considered. Voids due to large statistical fluctuations are indeed not detected by the kernel estimator. This characteristic of the kernel method is obviously relevant when regular distributions are sought for, but it introduces a bias if the genuine distribution exhibits such holes as shown in the following examples.

Whit an increase in the number of points, both methods appear to give quite similar results. The ISE distributions still differ, owing to the differences in sensitivity of the estimators to voids. This indicator also shows in a prominent way the ability of the kernel to reproduce almost perfectly the parent Gaussian distribution no matter what the experimental set is. But this disparity mostly disappears when the "noiseless'' set is considered; thus the wavelet estimator has a clear advantage, especially at a low mean number (see Figs. 5 (click here) and E6).

Example B

If we analyze two identical close Gaussians, it appears that the behavior of the two estimators is quite similar, both from the point of view of local variance and of the ISE distributions. This is a general result which is true also for the following examples. However, in both ideal "noiseless'' and experimental situations, the results show that the wavelet estimator is more efficient in the case of few events, and that this superiority vanishes when the number of points increases.

The explanation is easy. In the case of large data sets, the contrast between high and low density regions is reduced, and fewer and fewer simulations exhibit a strong gap between the two Gaussian peaks. Therefore, the wavelet transform finds it more and more difficult to exhibit the valley in the data distribution, and the median value and the "noiseless'' result accordingly increase between the two peaks, since a crucial piece of information for the wavelet-based restoration is missing. Conversely, the efficiency of the kernel estimator in detecting Gaussian peaks improves as the size of the data set grows, leading to a better peak-to-peak contrast.

Example C

This example clearly exhibits some consequences of the general behaviors pointed out just above. The key result of the test is that the small feature on the right side of the main curve is recovered only by the wavelet estimator. The feature is even more evident when a few number of points is involved in the estimate, the efficiency becoming lower as the sample size increases as pointed out before. Meanwhile, the asymmetry in the kernel estimate could be used to deduce the presence of a feature otherwise missed.

This discrepancy can be easily understood. It is very difficult for the kernel estimator to detect small features as it relies solely on the related small clusters of points to recover the signal. On the contrary, the wavelet estimator also detects the presence of voids, and such information is of great importance when broad small structures are sought for, which is the present situation. So it appears that the wavelet estimator does not recover the secondary peak only by relying on its points, but rather by also detecting the underdensity which separates it from the main structure. The contrast diminishes as the density increases; this explains why the secondary peak is blurred in the last high-density case (cf. example B).

Example D

A peaked small cluster has now to be recovered within a main Gaussian distribution. The smoothing caused by the use of kernel functions, as well as the ability of the wavelet-based method to make use of the gaps in the data sets are also exhibited here. In fact, although both estimators give correct and similar results when the number of data is high enough to define both structures properly, their respective behaviors are again different for a limited set of points. The wavelet estimator succeeds in exhibiting the secondary peak, even if its shape parameters are poorly determined, while the kernel estimate shows only a marked asymmetry for the "noiseless'' sample or a small deviation from the pure Gaussian for the experimental data set. The resulting variance is then lower for the wavelet estimate than for the kernel one.

These facts are not surprising. Both methods are sensitive to strong clustering and detect the secondary peak with increasing efficiency as the size of the sample increases. But, as said before, the use of kernel functions tends to smooth the data, so that small clumps are erased and real small voids are missed. On the other side, the wavelet transform enhances and makes use of both features, whatever their scales may be. This difference is striking when the sample with the smallest number of data is analyzed.

Example E

We have now to deal with a deep hole located within a constant high-density region. As shown by the variances and the ISE distributions, the wavelet estimate is better for recovering the hole, no matter what the size of the sample is. However, the kernel method also does a good job when the sample is not too small.

One can notice that the tails of the Gaussian hole are somewhat larger in the wavelet-based estimate than in the kernel one, and that the two small bumps which delineate the boundaries of the void are higher for the wavelet solution. These effects are related to rapid variations in the shape of the distribution and are very evident in the case of discontinuities. Both effects are due to the shape of the analyzing wavelet function which must be designed to yield zero-valued coefficients for a uniform distribution (see Fig. E9). In such a case, wavelet coefficients are indeed equal to zero, since positive contributions equal negative ones. But, as locations closer to a hole are examined, the density of points decreases in one part of the negative area of the function, yielding some positive values before ending with the negative ones denoting the void. Such artifacts are intrinsic to the wavelet method when a background is to be considered. This concerns obviously voids but also peaks superimposed on a constant background: two symmetrical positive or negative contributions appear, respectively. However, this effect is strong enough to generate significant structures and is a problem for further analyses only when the main structure is strongly contrasted with respect to the background or when the signal itself is very irregular. While negative features are unrealistic and can be easily thresholded by using a positivity constraint (see Eq. C6 (click here)), only a dedicated processing of the wavelet-based density estimate can allow one to remove them in a systematic way. Guidelines for doing so are given in the next section. Nevertheless, most of the cases of astronomical interest concern peaks located inside a low and nearly constant background (cf. introduction), so that the quite simple wavelet-based method described here can be used with great advantage in most situations without any particular difficulty.

3.5. General remarks

These examples enable us to make some general remarks about the way the kernel and wavelet density estimators analyze a discrete catalogue in order to recover the underlying density function.

Both estimators appear to give very similar results in most cases. In fact, the kernel makes use of a smoothing function whose size depends on the local density, while wavelets select the scale which is most appropriate for defining the local signal. However, kernel estimates fail to detect unambiguously faint structures superimposed on a larger component (example C) or poorly defined groups (example D, case 1). Conversely, wavelet-based solutions appear to find it difficult to accurately disentangle merged structures of comparable scale when the sample size is large (case 3, examples B & C). Moreover, the sensitivity of wavelets to voids generates negative values of the density which have to be thresholded, thereby inducing discontinuities at the zero-crossing locations. These voids correspond to strong gaps in the data or to regions with fewer than the minimum number of points required to compute a meaningful significance level. Finally, in all the examples, wider tails are generated by kernel estimates than by wavelet ones. Wide kernel functions are summed together in low density regions where no significant wavelet coefficients are usually found.

The kernel estimator takes into account only the presence of data, whereas the wavelet estimator relies on local over- and underdensities detection to restore the density function. Therefore, in the case of a restricted set of data or when dealing with very different mixed distributions, wavelets are more suitable than kernel functions, since two kinds of information about the local density contrast can be used. When these density contrasts are less prominent, the wavelet method may be less efficient than the kernel-based estimator. For instance, this may occur as gaps between close distributions disappear, owing to the increasing size of the data sample. On the contrary, the efficiency of the kernel solution always increases with the number of data points.

With regard to the void detection, the wavelet estimator performs better than the kernel one. But the solution obtained has two small symmetric artifacts which may cause false detections and have to be removed to allow fully automated analyses (this is also true for the other two estimators). An iterative solution is available within the wavelet framework, since this method enables one to restore separately each structure which constructs the density distribution function (see Rué & Bijaoui 1997; Pislar et al.  1997). The solution relies on a structure-based description of the signal. The main component has first to be detected and restored by using its wavelet coefficients. The obtained structure is then subtracted from the zero-th order density estimate (see Eq. 12 (click here)), and a new search for structures is performed until no more significant wavelet coefficients are detected. Alternate restorations are needed to accurately determine the shape parameters of close structures. In this way, the density estimate may be computed as a sum of genuine single structures.

In a forthcoming paper we plan to apply this procedure to two-dimensional sets of data to get a better analysis of the galaxy distribution within galaxy clusters. In fact, apart from a continuous density estimation, we are mostly interested in an accurate description of our data sample in terms of structures: cluster identification, evidence for subclustering, shape parameters with respect to theoretical models, etc. Nevertheless, Table 2 (click here) shows that the available information is already good enough to recover the main parameters of the underlying theoretical Gaussians involved in our examples, both for wavelet and for kernel estimators.

The kernel-based method could also be improved with a better identification of the optimal smoothing parameter by means of a more efficient data-based algorithm. This will result in a better density estimate from the point of view of either the resolution or the significance of the solution.

The same remark also holds for the MPL technique. However, the use of a more efficient minimization algorithm would be also needed in order to make this method faster and to improve its resolution. This is a necessary step for applying the method to multivariate cases.